基于MIMO-OFDM系统的盲源分离算法研究

丁 沿， 刘 甜， 张 琪

（河海大学 江苏 南京 211100）

频带利用率和多径衰落问题一直制约着无线通信的效率，如何解决这两个问题是未来无线通信系统的关键。MIMO无线通信系统通过在同样的频带中创建多个独立信道，使得信道容量随着发送和接收天线的数量的增加而线性增加，极大地提高了系统的频带利用率。但是MIMO系统的空间多路的方法产生的数据流所传输的信道不是正交的，并且接收到的数据流是混合的。在平坦衰落信道中，接收到的信号在时域上是发送的源信号的线性组合。但是在更加典型的现实环境中存在着多径效应，经过频率选择性信道后的信号在接收端产生码间串扰。在SISO系统中，为了解决这一问题优先的方法是使用串并转换，即将高速数据转换为低速率的子数据流，这些子数据流轮流通过OFDM技术复用到几个子载波上。这种方法有效地将频带划分为更小的能够被近似估计为具有平坦频率响应的子频带。在MIMO系统中使用频率选择性信道是一个公认的问题，并且使用OFDM调制信号是解决这一问题的一个可选的方法。MIMO和OFDM的结合被称为MIMOOFDM系统，并且是目前无线通信创新中的最优前途的领域之一，它目前被应用于802.11n无线标准。

在接收端有许多技术可以用来分离这些混合的平行数据流，并且通常他们依赖信道状态信息接收器的知识。最理想的数据恢复是当接收端没有关于信道状态信息的任何先验知识并且就好像数据通过未知的方式传输为前提来恢复数据,通过这种方式恢复源信号的过程被称为盲源分离（Blind Source Separation,BSS）。 文献[1]、[2]作为国内最早介绍盲源分离的文章，讲述了盲源分离提出的背景和意义，以及基本的原理和方法。文献[3]、[4]详细论述了盲源分离的研究现状和一些经典算法。文献[5]讲述了MIMO系统的忙均衡，涉及OFDM调制。文献[6]采用了Nyquist采样率，对MIMO-OFDM系统的接收信号进行采样，使用ICA对每一路进行分析。既然OFDM在频域中定义了，很自然的就需要在频域中考虑盲源分离的问题。本文尝试使用扩展FastICA算法，在频域对MIMOOFDM系统的接收信号进行盲源分离。

1 盲源分离理论

1.1 盲源分离基础

文献[4]中对盲源分离的定义是：从若干观测到的混合信号中提取、恢复（分离）出无法直接观测的各个原始信号的过程。这里的“盲”是指源信号未知，并且混合系统特性也事先未知或只知道少量的先验知识（如非高斯性、循环平稳性、统计独立性等）这两个方面。

盲源分离的数学模型可以表示如下：已知从多输入多输出（MIMO）非线性动态系统中测得传感器信号为X(t)=[x1(t)，x2(t)，…，xMr(t)]T，要求找到一个逆系统，以重构估计原始的源信号 S(t)=[s1(t)，s2(t)，…，sMr(t)]T。 源信号 S(t)未知，源信号如何混合得到观测信号也未知，盲源分离输出可由式（1）表达：

其中，A为信道混合矩阵，W为分离矩阵，G=WA为混合-分离/全局矩阵。如果G满足条件G=PD，则y(t)是混合信号被成功分离，其中P为置换阵，D为对角阵。

图1 盲源分离理论模型Fig.1 Blind source separation theory model

1.2 独立分量分析理论

独立分量分析[4]（Independent Component Analysis,ICA）是从多元（多维）数据中寻找其内在具有统计独立和非高斯的因子或成分的一种盲源分离方法。ICA主要用于解决盲源分离问题，在不知道源信号及混合矩阵的任何信息情况下，只需假设源信号是相互统计独立的，ICA就能很好地将源信号从混合信号中分离出来。

ICA的模型估计首先先选择一个合适的目标函数，然后对其进行最小化或最大化。因此，一个ICA方法的性质主要依赖于目标函数和优化算法两个方面。一般来讲目标函数的选取决定了ICA方法的统计性质，如一致性、渐变性、鲁棒性；最优化算法的选择则决定了算法的性质，如收敛速度、内存要求和稳定性等。

令x=(x1，x2，…，xn)T为n维随机观测向量，由n个未知源信号s=(s1，s2，…，sn)T线性组合而成。不失一般性，假设混合信号的随机变量和独立源都具有零均值。ICA线性模型的矩阵表示形式为：

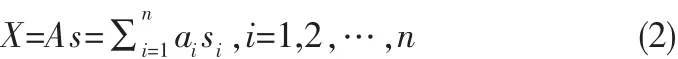
其中，si称为独立成分(Independent Component,IC)；A=(a1，a2，…，an)∈Rn×n为一满秩矩阵，ai称为混合矩阵；是混合矩阵的基向量。由此可知，各观测数据xi是由独立源信号si经不同aij线性加权得到的。进行ICA处理的目的就是找到混合信号x的一个线性变换矩阵W，使得输出尽可能的独立，即y(t)=Wx(t)=WAs(t)，独立源si也称为隐含变量，也就是说这些独立成分是无法直接观察到的；而混合矩阵A也是未知矩阵，唯一可利用的信息只有观测的随即向量x。ICA就是在某些限制条件下，根据x的统计特性，给出方程唯一解，实现独立成分的提取。

1.3 信号预处理

在对混合信号进行盲分离以前，由于可以利用的信息很少，通常都要先进行一些预处理,以降低分析难度。最常见的预处理过程有两个，一是去除信号的均值，有时也称为“对中”。另一个重要预处理过程是白化，有时又称为“圆整”。

在提出的大多数盲源分离算法中，都是假设源信号的各个分量是均值为零的随机变量，因此为了使实际的盲分离问题能够符合所提出的数学模型，必须在分离之前预先除去信号的均值。设π为均值不为零的随机变量，只需要用¯=x-E(x)代替x即可。在实际的计算中，通常使用算术平均代替数学期望，用来去除随机变量的样本的均值。 设 X(t)=(x1(t)，x2(t)，…，xn(t))T(t=1,2,…,N)为随机矢量x的N个样本，则采用以下的方法除去样本的均值，如式（3）:

1)由观测信号估计零时间延迟相关矩阵：Rxx(0)=E[x(t)x(t)T]。

2)对 Rxx(0)进行奇异值分解，得 Rxx(0)=U∧UT。

4)预白化信号与源信号之间的正交关系：z(t)=Qs(t)，其中Q=TA为一正交矩阵。

1.4 目标函数的选择

本文选取基于峭度的目标函数方法，对信号进行盲分离处理。对一个随机变量y的峭度的定义如式（4）：

由中心极限定理知，一组值和方差为统一数量级的随机变量叠加的结果必接近高斯分布。因此，如果观测信号是多个独立源的线性组合，则观测信号比源信号更加接近高斯分布，其峭度与源信号相比，更接近零值。盲源分离的目的就是通过迭代找到一个分离矩阵W，使得恢复信号Y=WHX的各个分量的峭度值远离零值，这样分离出的信号Y就是源信号S的估计。

通过IFFT方式调制后的信号是复数信号，将峭度的概念扩展到复数域后得到的峭度定义公式如式（5）所示。

其中y′是复数随机向量。

为了使得目标函数的收敛计算更具有鲁棒性，通常选择合适的非线性函数G(y)来替代y，文献[7]给出了如下几个比较有效的非线性函数：

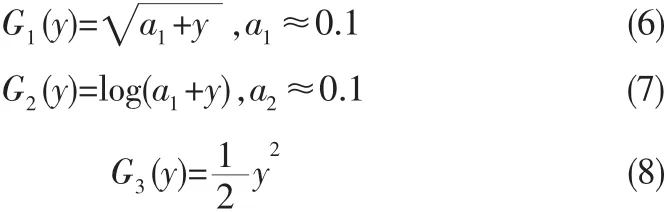
2 MIMO-OFDM系统模型

本文采用的MIMO通信系统的结构是采用多发射机和多接收机的方式来提高频带利用率，而没有使用空间编码。通常，独立平行数据流通过Mt个天线发送和Mr个天线接收。在基带等效的情况下，每个发送天线发送信号st(t)，接收天线收到一个显著的信号xr(t)，其中下标t，r,表示相应的发送天线和接收天线。在平坦衰落环境中，发送端和接收端信道系数表示为hrt，表示从第t个发送端传送到第r个接收端。MIMO信道模型如图2所示。

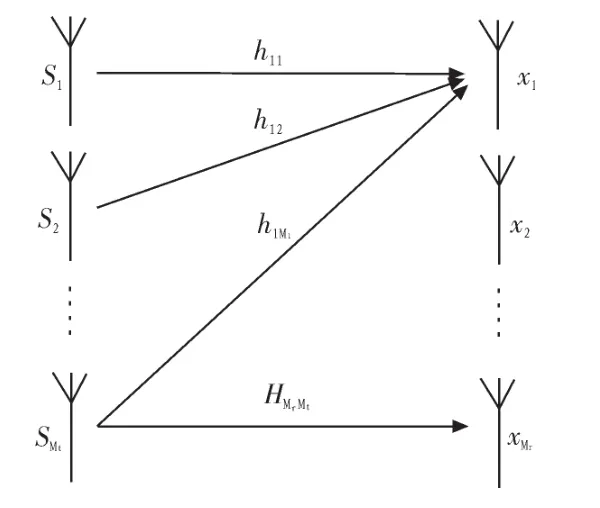
图2 MIMO信道模型Fig.2 MIMOchannel model

在这一系统中，首先不考虑信道噪声，MIMO系统的输入和输出的关系可以通过时域中的一组线性方程组来表示，如下式（9）：

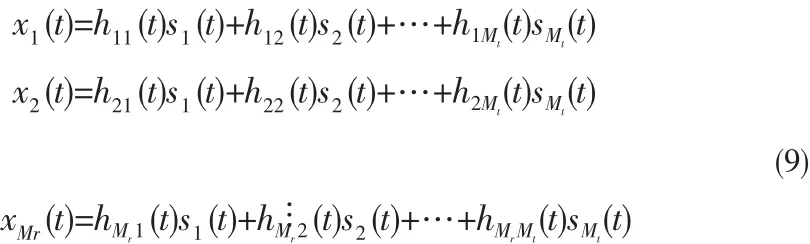
在一个真实的无线通信环境模型中，每一个信号通路是服从多径衰落的。多径衰落信道如下图3所示，一个单发送和单接收天线对，假设MIMO系统的多径阶数为L，则hrt(l)(L=0,1,…,L-1)表示第t个发送天线到第r个接收天线的第l径的时域冲击响应，所以接收信号xm(t)可以表示为如式(10)：

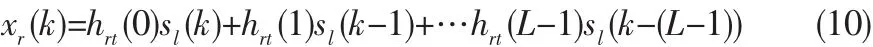
其中L是信道多径阶数，k是离散数据信号。

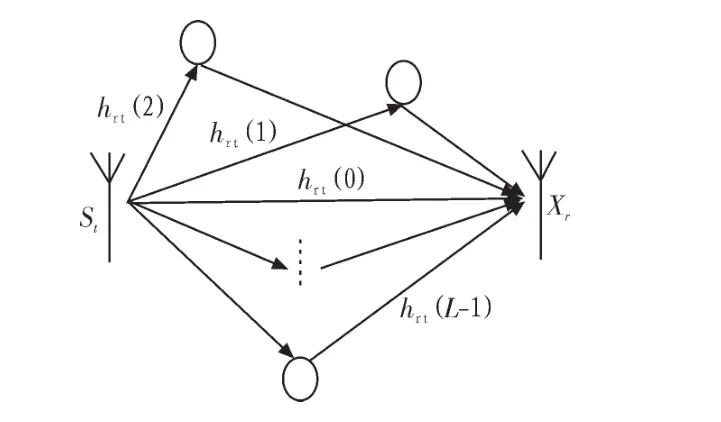
图3 SISO系统多径传输模型Fig.3 SISO system multipath transmission model

对 hrt(l)(L=0,1,…,L-1)补零成为序列{hrt(0),hrt(1),hrt(2),…,hrt(L-1),0,…,0}，并作N点傅里叶变换可以获得天线对(t,r)之间的信道响应矩阵为：Hrt=[Hrt(1),Hrt(2),…,Hrt(N)]，即：

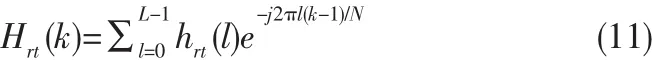
在具有N路子载波的MIMO-OFDM系统模型中，正如图4所示,k=1,…,N是第t个发送天线发送的数据符号，它可以是通过M-QAM或MPSK调制的，不同的子载波k可以采用不同的调制方式。

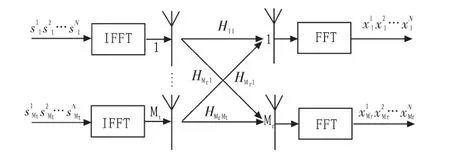
图4 MIMO-OFDM信道模型Fig.4 MIMO-OFDM channel model

IFFT和FFT操作用来生进行OFDM调制，添加循环前缀后组成OFDM数据帧，考虑到一个具体的OFDM副载波的隔离。以第k路举例来说，发射天线的第k个子载波的发射信号向量为S(k)=[s1(k),s2(k),…,sMt(k)]T：，接收天线端接收到的第k个子载波信号为：X(k)=[x1(k),x2(k),…,xMr(k)]T，第k个子载波的信道响应可以表示为：

结合式(9)推导出如下关系式(13)：

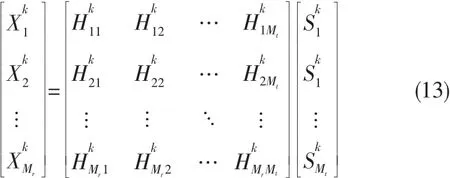
其矩阵形式如式（14）：

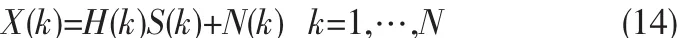
其中N(k)是Mr×1维的零均值加性高斯白噪声。

3 FastICA算法在MIMO-OFDM源信号分离的应用

目前人们对FastICA盲源分离算法的研究主要集中在非频选的MIMO时域信道中，本文运用MIMO-OFDM技术，将扩展FastICA算法应用到MIMO-OFDM系统的盲源分离中。具体思想如下：

假设信道长度为L，采用循环前缀的长度为Ncp，当满足Ncp＞L时，第k个子载波所传输的数据向量S(k)=[s1(k),s2(k),…,sMt(k)]T可以认为经历了平坦衰落的MIMO信道。接收端接收到的数据经过FFT解调后，得到的第k个子载波的数据向量为X(k)=[x1(k),x2(k),…,xMt(k)]T，那么我们可以通过MIMO频率非选择衰落信道下的FastICA算法进行盲信号分离。

假设MIMO-OFDM系统的子载波数为N,取b帧的OFDM符号，那么在接收端经过FFT解调和去除循环前缀后的第i(i=1,2,…,b)帧的信号可以表示为：

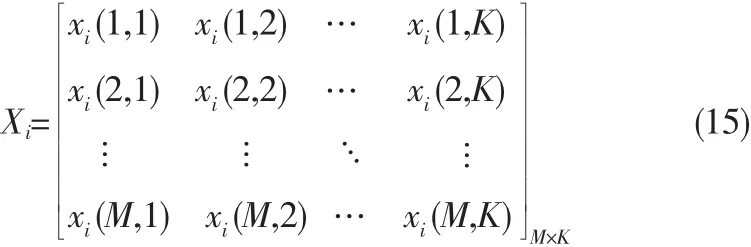
那么第k个子载波的数据块可以表示为：

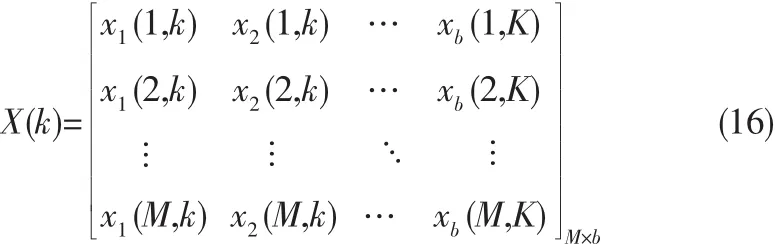
由于各个子载波之间相互正交，互不干扰，每一路子载波都进行同样的ICA处理，在此本文仅以第k个子载波数据块X(k)为例,运用FastICA算法，进行盲信源的分离。

分离矩阵迭代公式为式(17)：

其中 H 是共轭转置变换，g(·)和 g′(·)分别是非线性函数的一次和二次导数。

4 仿真

为了证明本文提出的盲源分离方案的性能，选取Mt=Mr=2，即两个发送天线和两个接收天线的MIMO系统。OFDM调制采用子载波数N=64，每一路子载波上的数据都采用4QAM的调制方式，信道阶数L=8，循环前缀长度Ncp=16，OFDM数据帧个数b=50。时域到频域之间的转换采用64点FFT,生成了64个信道矩阵，每一个信道矩阵对应一个子载波。在信道矩阵混合数据符号之后，对每一路数据流添加加性高斯白噪声。k=32路子载波频域混合信道响应为:

图5分别展示了以第k=32路子载波为例的发送数据源、信道混合矩阵混合后和FastICA算法分离后恢复的数据的星座图。

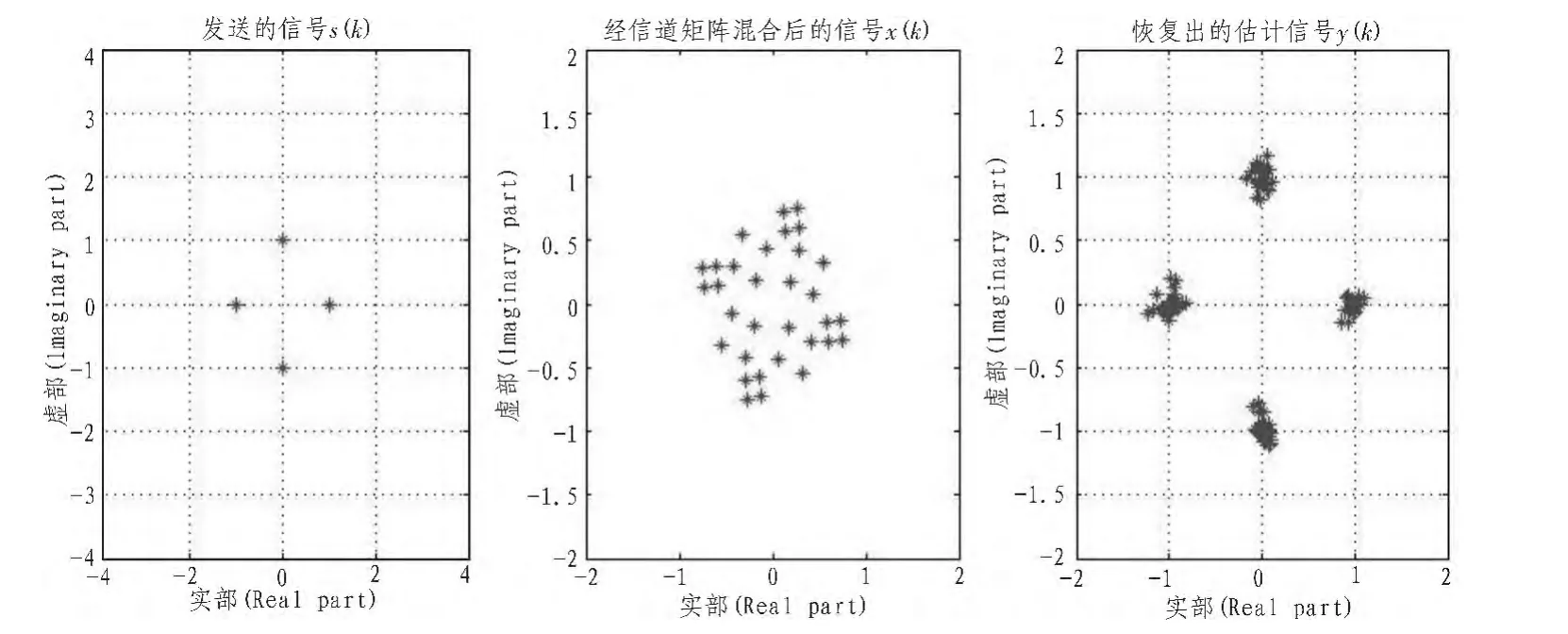
图5 发送信号、混合信号和恢复信号的星座图Fig.5 Constellations of Original、mixed and recovered signals

5 结论

仿真结果表明，本文提出的基于复数数据的扩展FastICA算法能够有效处理MIMO-OFDM系统的源信号的分离，并且算法收敛的速度也比较快。

[1]张贤达，保铮.盲信号分离[J].电子学报，2001（S1）:1766-1771.ZHANG Xian-da，BAO Zhen.Blind signal separation[J].Chinese Journal of Electronics，2001（S1）:1766-1771.

[2]李小军，朱孝龙，张贤达.盲信号分离研究分类与展望[J].西安电子科技大学学报，2004（3）:399-404.LI Xiao-jun，ZHU Xiao-long，ZHANG Xian-da.Blind source separation:classification and frontiers[J].Journal of Xidian University，2004（3）:399-404.

[3]王卫华.盲源分离算法及应用研究[D].哈尔滨:哈尔滨工程大学，2009.

[4]余先川，胡丹.盲源分离理论与应用[M].北京:科学出版社，2011.

[5]Zarzoso V，Nandi A K.Blind MIMO equalization with optimum delay using independent component analysis[J].International Journal of Adaptive Control and Signal Processing，2004（18）:245-263.

[6]Obradovic D,Madhu N,Szabo A,et al.Wong.Independent component analysis for semi-blind signal separation in MIMO mobile frequency selective communication channels[C]//in Proc.of the In.Joint Conf.on Neural Networks,IEEE，2004（1）:53-58.

[7]Bingham E,Hyvarinen A.ICA of complex valued signals:a fast and robust deflationary algorithm[J].in Proc.of the In.Joint Conf.on Neural Networks，2000（3）:357-362.