水下航行体无刷电动舵机仿真研究

吕赟

（昆明船舶设备研究试验中心 云南 昆明650010）

舵机作为伺服执行机构，其作用是根据航行体控制电路输出的一定大小和极性的信号，操纵水下航行体的舵面，以便控制水下航行体的航行，常用的舵机系统可以分为液压舵机、气动舵机及电动舵机。液压舵机和气动舵机结构复杂、加工精度要求高、质量大、成本高。电动舵机则具有较好的输出力矩，抗负载能力和频率响应,并且结构简单、可靠性高。在早期的电动舵机中，由于直流电机的转矩相应快，调速性能好，成为电动舵机的主要选择，但直流电机采用机械换相，机械寿命差，会给航行体的可靠性带来隐患。无刷直流电机是近几十年随着电力电子技术的迅速发展而发展起来的一种新型电机。跟传统的直流电机相比，无刷直流电机具备很多优势：效率高，并且没有电刷等机械换向装置，不用考虑换向器机械强度及电刷磨损问题，大大提高了使用寿命和可靠性。这些优良特性使无刷直流电机更适合应用于电动舵机系统，因此研究基于无刷直流电机的电动舵机系统具有重要意义[1]。

为了准确预测电动舵机及伺服控制系统的运行性能，本文在分析了电动舵机的数学模型后，利用Matlab/Simulink为其建立了闭环PID控制模型，该仿真模型具有良好的起动和抗干扰性能，对电动舵机控制系统的实际开发有重要的借鉴意义。

1 电动舵机数学模型分析

电动舵机以电为动力源，主要由控制器、无刷直流电机、减速传动机构和反馈电位计组成，其中控制器一般采用PID控制，以满足舵机的动静态指标要求,如图1所示。

图1 电动舵机工作原理Fig.1 The working principle of the electric steering gear

1.1 无刷电机数学模型

式中 Ua、Ub、Uc为三相绕组的相电压，Ra、Rb、Rc为三相绕组的相电阻，ia、ib、ic为三相绕组的相电流，Laa、Lbb、Lcc为三相绕组的自感，Mab为A相和B相绕组间的互感，其他亦然。Ea、Eb、Ec为三相绕组的反电势。

对于永磁体转子凸装式结构，与一般的电机不同，可以忽略凸极效应，因此“定子”三相绕组的自感为常数，三相绕组间的互感也为常数，两者都与转子的位置无关。因此可做如下假设：

因为定子三相绕组为Y型连接所以：

因此可以得到简化的电压方程为：

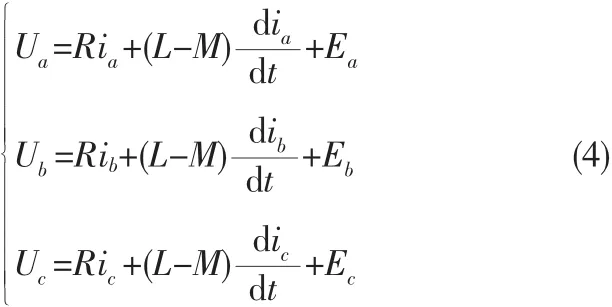
由电机学可知，在理想情况下永磁无刷直流电动机的电磁转矩为：

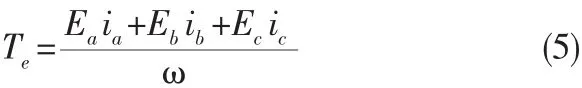
电机的机械运动公式为：

Jr为电机转子的转动惯量，Te为电机的电磁转矩，ω为电机转子转速 （机械角速度），Tl为电机转子的负载转矩，Kb为转子对轴承的摩擦系数。

1.2 减速传动机构数学模型

本文采用滚珠丝杠作为舵机减速传动机构，与其他减速器相比，滚珠丝杠具有减速比范围大，高精度、高效率、高刚度、运行平稳等特点优点。滚珠丝杠传动的物理基础是滚动摩擦，工作原理为：滚珠丝杠与滚珠螺母之间填满了滚珠，在滚珠螺母上有与滚道始末接通的滚珠回珠孔，当丝杠转动时，滚珠即沿着滚道作循环运动，螺母作直线运动。因为是滚动摩擦，所以摩擦小，传动效率高[2]。

为维护法律监督的严肃性，审判机关应参照诉讼程序处理检察建议所涉事项。具体程序设计可以为：收到检察机关提出检察建议三日内，审判机关的审判监督部门应当受理；受理后三日内，应当向相关部门或人员告知检察建议涉诉事项，要求其七日内提出意见建议并调取案件材料；相关部门或人员提出意见建议或逾期未提出意见建议的，审判监督部门于十五日内根据调查结果提出处理意见经审判委员会讨论决定后向检察机关作出书面回复，写明对检察建议所涉事项的调查及处理情况；检察机关与审判机关就检察建议所涉事项认识不一致的，分别上报一级机关处理；检察机关与审判机关就检察建议所涉事项认识一致的，启动案件终结程序。

滚珠丝杠减速传动机构的工作原理如图2所示。

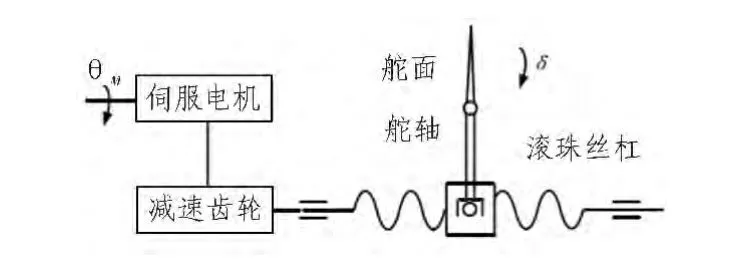
图2 舵机滚珠丝杠原理Fig.2 Servo ball screw principle

减速传动机构工作时，丝杠每转动一周，螺母沿丝杠移动一个导程，舵轴带动舵面转动一个角度，若电机转动的转速ω，θm为电机转过的角度=ω，那么舵面转动的角度δ为：

其中Lg为滚珠丝杠的导程，i为减速比，r为拨叉的有效转动半径。

2 电动舵机仿真模型搭建

作为电动舵机的核心部件，本文利用Matlab软件提供的Power system block工具箱进行无刷电机建模仿真,这种情况考虑了电机换相换流情况，更接近实际电机的运行状态，以下将介绍各模块的建立方法。

2.1 电机模型

无刷电机本体模型在整个控制系统的仿真模型中是最重要的部分，根据式(4)可得无刷直流电机本体仿真模型如图3所示。

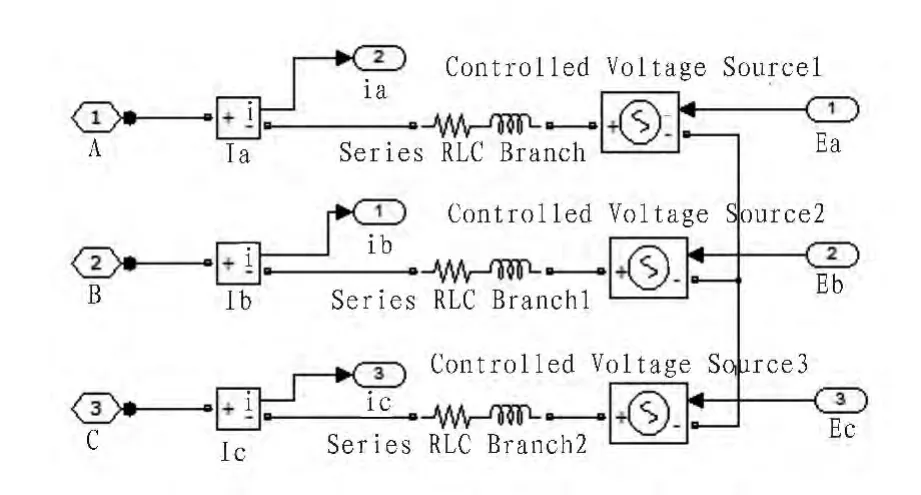
图3 电机本体仿真模型Fig.3 Motor simulation model

2.2 驱动器模型

驱动器对于无刷直流电机来说，也就是电子换向器，并且还具有PWM调节的功能。对逆变器的建模，本文采用Matlab的SimPowerSystem工具箱提供的IGBT模块建立三相逆变器[2]。逆变器根据控制信号，按照一定顺序导通和关断，进而驱动无刷电机转动。

2.3 反电势模型

无刷直流电机电枢绕组中的反电势波形与气隙磁场强度Bm、电机转速ω、电机极对数p、每相有效串联匝数W、电子电枢内径Da、轴向导体有效长度L和转子位置角θ有关。120°电角度的梯形波反电势具有周期性和对称性，由傅里叶级数分解波形，可得三相反电势波形的表达式[3]：

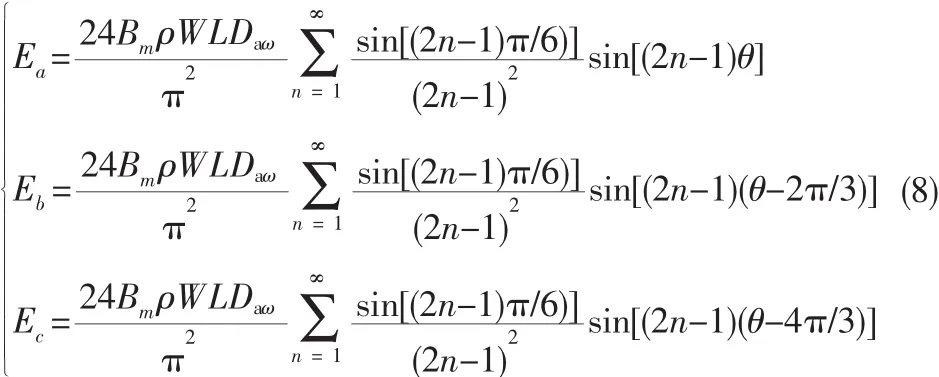
根据三相全桥电路IGBT的开通关断顺序编写位置信号函数(s1，s2,s3)=f(θ)。 由式(2)建立 S-function 模块 emf.m 文件，模块输入为电机直轴与定子A相绕组轴向夹角、电机转子角速度和电机参数 Bm、P、W、Da、L, 输出为三相反电势 Ea、Eb、Ec及电机位置信号 s1，s2，s3。

2.4 转矩和转速模型

根据无刷直流电机数学模型中的电磁转矩方程式（5），可以建立转矩计算模块，模块输入为三相相电流与三相反电动势，通过加、乘模块并除以转速ω即可求得电磁转矩信号Te。根据无刷电机的机械运动方程式(6)，由电磁转矩、负载转矩以及摩擦转矩，通过加乘、积分环节即可得到转速信号。

2.5 减速机构模型

减速机构模型反映的是电机转速与舵面角度的关系，由公式（7）可得，减速传动机构的仿真模型如图4所示。

图4 减速传动机构仿真模型Fig.4 Deceleration mechanism simulation model

2.6 反馈电位计

反馈电位计反映舵机输出角度与反馈电压值之间的关系，其模型是一个比例环节，本文中的反馈电位计传递系数为0.2。

2.7 双闭环PID模型

本文中的舵机伺服控制系统由位置外环和电流内环二者共同串联构成，输出值通过改变PWM脉宽控制器的占空比，产生方波脉冲控制信号，经三相逆变器驱动电路，实现对无刷电机的控制。这样系统不仅能控制舵机输出角度，而且能控制电流，充分利用电机的过载能力，获得较快的动态响应，以及良好的静、动态品质[4]，如图5所示。

3 仿真和结果分析

综合第二节所述各子模块的原理，并在Matlab/Simulink下分别为其建立子系统，最终得到的无刷电动舵机伺服系统的模型如图6所示。

图5 双闭环PID控制器Fig.5 Double-loop PID controller

图6 电动舵机伺服控制系统模型Fig.6 Electric steering servo control system model

以某型样机为分析对象，上述模型中的参数设置为：定子相绕组电阻R＝1Ω，定子相绕组自感L＝0.02 H，互感M＝0.002 1 H， 转动惯量 J＝0.004 kg·m2， 阻尼系数 B=0.000 31 N·m·s/rad，额定转速 n＝3 000 r/min，极对数 p＝2，24 V 直流电源供电。减速齿轮减速比100，滚珠丝杠导程Lg=0.02 mm，得到的仿真曲线如图7和图8所示。

图7为舵机对位置阶跃信号的响应曲线图，由图可以看出，在参数选择适当的情况下，舵机控制系统响应时间快，无超调；图8为舵机控制系统对正弦输入信号的跟踪曲线图，可以看出该舵机系统对输入的正弦信号跟踪响应迅速，平稳，证明该仿真模型准确，可以准确预测电动舵机控制系统的运行性能[6]。

4 结论

本文以电动舵机的数学模型为基础，在Matlab/Simulink环境下结合S-函数对舵机系统进行了建模，搭建了其闭环PID控制系统[7-8]，最后通过对样机的仿真来验证系统模型，仿真结果表明：波形符合理论分析，系统响应快、稳态性能好，在该仿真模型基础上，可以方便快捷地实现多种控制策略，加快实际系统设计开发的过程，提高开发效率。

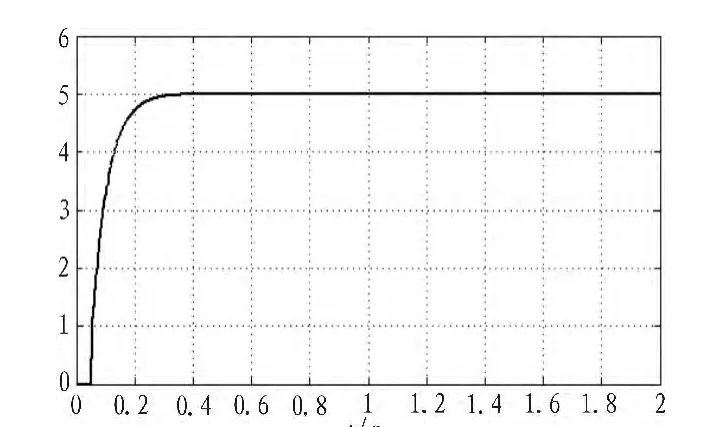
图7 舵机位置阶跃响应曲线Fig.7 Servo position step response curve

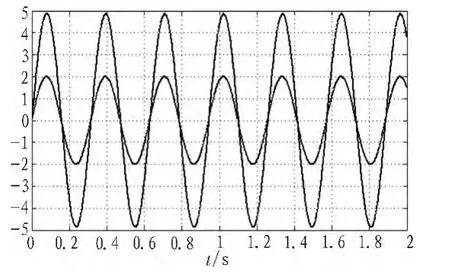
图8 舵机正弦信号跟踪曲线Fig.8 Servo sinusoidal signal traces

[1]郭庆鼎，王成元，周美文，等.直线交流伺服系统的精密控制技术[M].北京：机械工业出版社，2000.

[2]孙树扑，李明，王旭光，等.电力电子技术[M].北京：中国矿业大学出版社，1999.

[3]李宁，陈桂.运动控制系统[M].北京：高等教育出版社，2004.

[4]周绍英，储方杰.交流调速系统[M].北京：机械工业出版社，2001.

[5]梁晓庚，王伯荣，余志峰.空空导弹制导控制系统设计[M].北京：国防工业版社，2006.

[6]祁大勇.电动伺服舵机的研究[D].北京：北京理工大学出版社，1994.

[7]鲁雄文.模糊PID控制系统的设计与研究[J].现代电子技术，2014（24）：146-149.LUXiong-wen.Research and design of fuzzy PIDcontroller[J].Modern Electronic Technique，2014（24）：146-149.

[8]窦艳艳，钱蕾，冯金龙.基于Matlab的模糊PID控制系统设计及仿真[J].电子科技，2015（2）：119-122.DOU Yan-yan，QIAN Lei，FENGJin-long.Design and simulatiom of a fuzzy PID controller based on Matlab[J].Electronic Science and Technology，2015（2）：119-122.