基于最小二乘的航天器天文导航定姿算法研究

王易南，闫 杰，温 琦

（西北工业大学 航天学院，陕西 西安 710072）

准确的导航信息是航天器顺利完成入轨、变轨、飞行，实施对地观测、对地通信、信号转发等各种空间任务的重要保障。姿态信息是导航信息的重要组成部分，姿态信息由姿态敏感器测量确定。目前，空间探索活动越来越频繁，卫星技术越来越复杂，新时期空间事业的蓬勃发展对姿态测量提出了越来越高的要求。星敏感器是目前精度最高的姿态测量仪器之一，其中自主导航星敏感器具有独立性高、稳定性好的特点，是目前航天导航领域的研究热点。航天器姿态确定问题归结为利用矢量观测的Wahba问题，研究最小二乘法对星敏感器的测量信息进行处理得到航天器姿态信息[1]。

1 星光定姿问题

目前，航天器上应用的姿态敏感器种类很多，如三轴磁强计、太阳敏感器、地平仪以及星敏感器等，而这些基于矢量观测的姿态确定问题又都可以归结为Wahba问题。在1965年，Wahba提出利用矢量观测信息确定航天器的姿态问题，其核心是求解优正交矩阵R，使得损失函数[2]

达到最小。几十年来，人们提出了许多基于矢量观测求解姿态的算法，这些算法基可以分为两大类：一类是确定性方法，另一类是结合星敏感器测量数据和陀螺测量数据/或动力学模型的状态空间估计方法。

2 基于最小二乘的星光定姿算法

最小二乘法经理了100余年的发展和考验已经成为许多领域多种类型数据处理的最广泛使用的方法，最小二乘的数学模型简洁方法也比较简单。设被估计的量是n维矢量，即[3]：

对n维矢量的估计需要对X进行观测，假定对X进行了k次观测，观测方程：

观测方程简记为：

最小二乘法的准则J最小：

求导：

令上式为零得到估计值：

误差矢量：

噪声的均值为 E[V]，方差假定为 R=E[（V－E[v]）（V－E[v]）T]，估计值误差性质：

完成星图识别后，可以得到每颗星的星光观测矢量bi和导航星惯性矢量ri，然后可以计算出性敏感器三轴在惯性空间的姿态矩阵。

设有m≥3颗观测星被识别，这些星在星敏感器本体坐标系和惯性坐标系中的单位矢量分别为Ui=（，，）t和vi=（xi，yi，zi）t，记星敏感器本体坐标系的三根坐标轴 X、Y、Z 在惯性坐标系中的单位矢量分别为[4－6]：

即姿态阵为：

则有：

或者：

令：

则有：

如果 m=3，则有：

如果m＞3，只要V列满秩，则由最小二乘法有：

由上式计算出姿态阵后，进行单位向量检查：当识别结果正确时，所得姿态阵应为符合笛卡尔坐标系的单位正交阵。如果姿态阵中|lx|、|ly|或|lz|与1相差较大，表明识别为误识别。 如果|lx|∈[0.99，1.01]且|lz|∈[0.99，1.01]，则认为通过检查，程序继续进行对姿态阵的正交化过程；否则判为误识别退出。

正交化后的姿态阵A*的计算公式如下：

由于全天自主恒星识别过程中发生误识别的概率要较高，必须对识别结果进行检验。

根据以上原则对姿态确定结果进行如下检验：以姿态阵的lx与ly进行叉乘，所得结果与lz轴比较，如符号相同表面为右手坐标系，表明识别正确；反之为左手坐标系，表明识别错误。

上述过程即可求解得姿态矩阵，与星图模拟中的旋转矩阵相比较即可得识别算法的误差。

3 仿真及分析

3.1 仿真流程

数字仿真的流程如图 1所示，其中星图模拟中星敏感器CCD技术参数见表1。原始星表为SAO星表，采用6.0等作为星敏感器的星等敏感极限，选取亮度高于或等于6.0的5 103颗星组成导航星表，经过筛选导航星表有3 278颗星，对角距小于30″的双星进行合成处理，30″～0.1°的删除处理，得到导航星表。星图匹配算法采用K矢量加星棱锥算法，选择星角距作为星特征。对模拟生成的星图进行星图预处理和特征提取，具体包括：分离星像和背景、星像与星像分离和质心提取。图 2、图 3分别是不同赤经、赤纬下的数字模拟的星图。

图1 仿真流程Fig.1 The process of the simulation

表1 星敏感器CCD光学参数取值Tab.1 CCD optical parameters of the star tracker

3.2 星光定姿

经过星图匹配，采用最小二乘法（18）或（17）对星敏感器测量进行处理，得到航天器姿态信息，图 4和图 5分别是赤经、赤纬误差，可以看出误差在角秒级。

4 结 论

采用经典的最小二乘法对某型号工程中天文导航星光定姿方法进行研究，通过数字仿真证明姿态精度可以达到角秒级，而且算法实现简单可行，运算效率高。对后续研制任务具有理论参考意义。

图2 模拟星图Fig.2 Simulation of the star maps

图3 模拟星图Fig.3 Simulation of the star maps

图4 星光定姿赤经误差Fig.4 The right ascension error

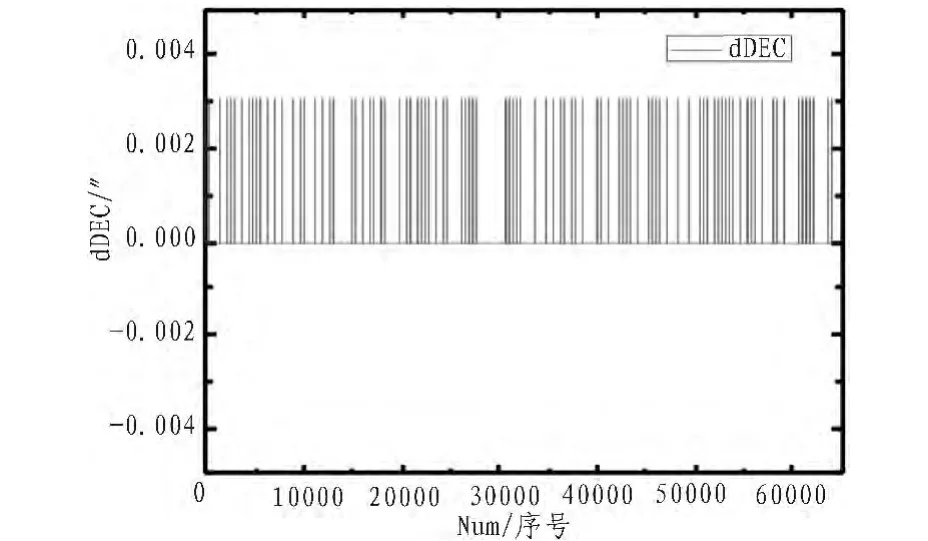
图5 星光定姿赤纬误差Fig.5 The declination error

[1]De Cou，A.B.Spacecraft Attitude Measurement Using Spatial Coherence of Laser or Star Light[J].IEEE Transactions on Aerospace and Electronic Systems，1971， AES－7 （2）:288－298.

[2]张力军.基于多视场星敏感器的航天器姿态确定方法研究[D].长沙：国防科学技术大学，2011.

[3]宋亮亮，张涛，梁斌，等.基于星敏感器的卫星姿态确定方法研究[J].系统仿真学报，2010，22（S1）:1-6.SONG Liang-liang，ZHANG Tao，LIANG Bin，et al.Attitude determination method based on star sensor[J].Journal of System Simulation，2010，22（S1）:1-6.

[4]张晨.基于星跟踪器的航天器姿态确定方法研究 [D].武汉：华中科技大学，2005.

[5]王鹏.基于星载敏感器的卫星自主导航及姿态确定方法研究[D].哈尔滨：哈尔滨工业大学，2008.

[6]矫媛媛.基于星敏感器/陀螺组合测量的卫星姿态确定方法研究[D].长沙：国防科学技术大学，2007.