基于排队论的机动车道数量设计探索

□ 李 京 李 丽

一、引言

近年来随着国家经济突飞猛进式的增长，汽车保有量也随之急剧上升，城市道路车流量已趋于饱和，北京市政府采取了多种措施以缓解交通拥堵如限行、摇号等，但仍然无法改善城市中心拥堵的现状，所以进行机动车道数量的设计也是缓解交通拥堵的一种好的方法。机动车道作为交通运输系统中最为重要的载体，在道路的通行能力上拥有着举足轻重的地位，而车道数量是其宏观设计的主要指标，如果车道数量不适应现有机动车流量，它就会成为交通硬件上的一个瓶颈，那么就会发生通行率低以至于堵塞的后果。所以本文通过排队论模型对机动车道数量进行合理的规划设计，以充分发挥车道的基本作用。

二、排队论概述

(一)排队论概念及发展。排队论是研究“服务”系统因“需求”拥挤而产生等待行列及排队的现象，以及合理协调“需求”与“服务”关系的数学理论，也称随机服务系统理论［1］。最早有关排队论的著作是1909年尔兰发表的电话交换机使用情况的论文;第二次世界大战之后运筹学得到了蓬勃的发展，排队论的论述已十分普及;二十世纪六十年代，排队论的研究日趋复杂，在应用方面进入到了交通、生产、服务方面［2～4］。凡是出现拥堵现象的领域，都可以运用排队论［5］。在道路交通系统中就存在大量的排队现象，如信号灯、公交站、收费站［6～8］等。本文即以排队论为基础，对机动车道数量进行深入研究。

(二)排队论系统。一般的排队系统都有三个基本组成部分［9］:输入过程;排队规则;服务机构。图1则为机动车道排队系统的一般模型。

输入即指顾客到达排队系统。顾客的总体组成分为有限型与无限型，机动车源源不断地到达特定的机动车道，可以看作是总体为无限型。顾客相继到达的时间间隔有确定型和随机型两种，显然通过路口的机动车到达时间不可预测，因此是随机型的。

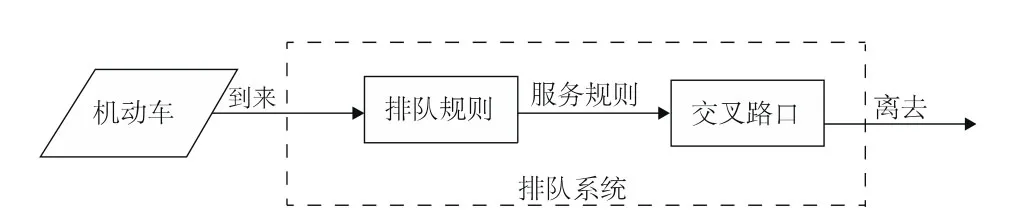
图1 机动车道排队系统一般模型

排队规则分为即时制与等待制，机动车道上的汽车流期望通过路口就必须坚持到服务为止，因此属于后者。且机动车按次序依次通过，符合先到先服务原则。

服务机构根据机动车道数量排队系统可分为单队－单服务台情形与多队－多服务台情形，即单机动车道机构与多机动车道机构。和输入过程类似，服务时间分为确定型与随机型，显然机动车因避让行人、交通拥堵、信号灯变化使得通过路口的时间各有差异，所以此研究的服务时间为随机型。

三、排队论模型

(一)单机动车道排队模型。图2为单机动车道排队模型，即M/M/1///FCFS模型。

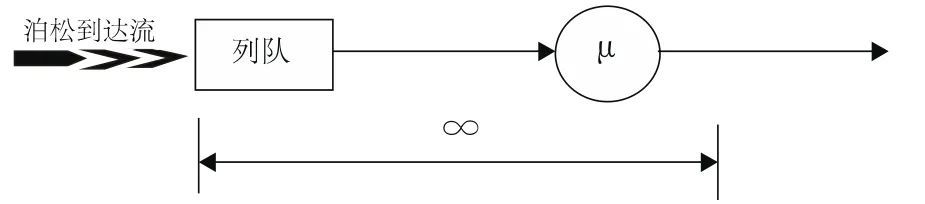
图2 单机动车道排队模型

基本假设:机动车到达服从泊松分布，平均到达速率为λ(λ＞0)，相邻两辆车间隔时间为1/λ，机动车数为∞;服务时间相互独立且服从负指数分布，接受服务的输出率为μ(μ＞0)，对每辆机动车的服务时间为1/μ;一条机动车道;系统容量为∞。

指标:交通强度ρ=λ/μ。当ρ＜1时，在时间充分的条件下状态稳定，此时的交通顺畅;当ρ≥1时，状态不稳定，队会越来越长，呈现拥堵状态。由差分方程与little公式等可推出以下公式:

系统中没有机动车的概率:

系统中有n辆机动车的概率:

系统中的平均机动车数:

队列中等待的平均机动车数:

系统中机动车平均逗留时间:

队列中机动车平均等待时间:

(二)多机动车道排队模型。图3为多机动车道排队模型，即M/M/N///FCFS模型。

图3 多机动车道排队模型

指标:P=λ/Nμ。假设机动车道数N＜系统中车辆数n。

系统中没有机动车的概率:

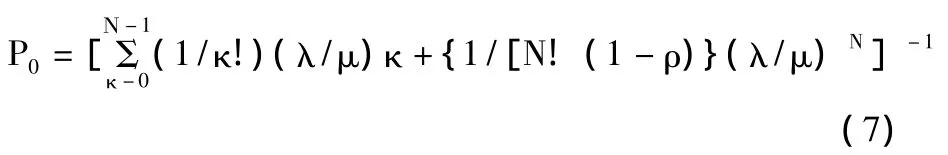
系统中有n辆机动车的概率:

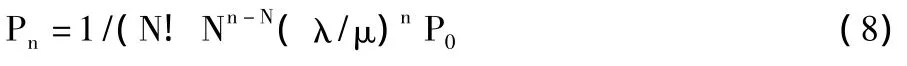
系统中的平均机动车数:

队列中等待的平均机动车数:

系统中机动车平均逗留时间:

队列中机动车平均等待时间:

四、数学模拟分析

假设一个单向路口的车流量为900L/h，考虑延迟因素和驾驶员理想状态通过，每辆车通过时间为10s，对此模拟路口进行机动车道数设计。

单机动车道排队模型:

λ =900/3600=0．25，μ =1/10=0．1，ρ =2．5 ＞1，此方案不成立

多机动车道排队模型:

N=2:λ =0．25，μ =0．1，ρ =0．25/(2*0．1)=1．25，此方案不成立。

N=3:λ =0．25，μ =0．1，ρ =0．25/(3*0．1)=0．83 ＜ 1，此方案成立。

Ρ0=0．172，L5=15．210，Lq=12．170，W5=60．841，Wq=48．680。

N=4:λ =0．25，μ =0．1，ρ =0．25/(4*0．1)=0．625 ＜1，此方案成立。

P0=0．612，L5=6．923，Lq=4．423，W5=27．692，Wq=17．692。

N=5:λ =0．25，μ =0．1，ρ =0．25/(5*0．1)=0．50 ＜ 1，此方案成立。

Ρ0=0．832，L5=3．268，Lq=0．768，W5=13．072，Wq=3．072。

数据结果的比较如图4、图5所示。

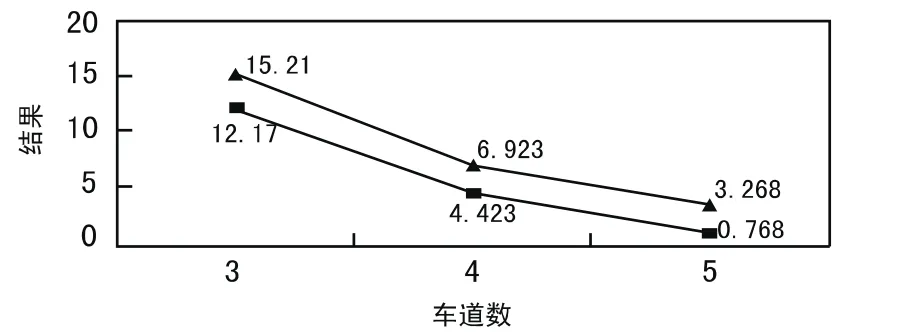
图4 当车道数分别为3、4、5时Ls、Lq值

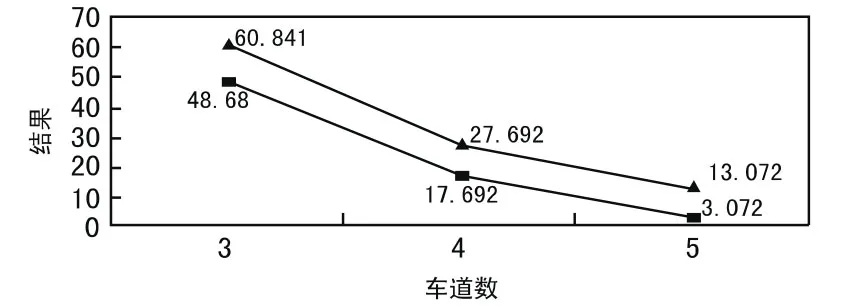
图5 当车道数分别为3、4、5时Ws、Wq值

通过模拟分析，发现N=1或2时，ρ＞1，排队过长，为不稳定状态，方案不成立;当N=3、4、5时，ρ＜1，呈稳定状态，模型畅通，方案都成立。从表1、表2体现出的数据中，显然机动车道数越多，排队中的车辆越少，等待的时间越短。但是从数据变化折线的斜率可以看出，车道数从3变为4时，平均等待时间与平均等待机动车数的下降速率是显著提高的，而车道数从4变为5时，这几个指标的变化率相比之前显著减少。结合现实中经济成本方面考虑，每增加一条车道数需要占用更多的土地与资金成本。所以从此数学模拟综合分析，机动车道数为4时基本能够满足交通比较顺畅，经济方面比较适中，因此选择建设4条机动车道的方案。

五、实例评价

选取北京市海淀区五道口展春园西路作为实验数据测量地点，选早高峰为待测时间间隔(此路段在由南向北方向有3条机动车道)。表1为在8:00～8:30的时段中每5分钟所通过的机动车辆数，表2为在红灯亮时及红灯没有亮时分别随机取得的4辆机动车的通行时间。

表1 每时段通过的机动车辆数

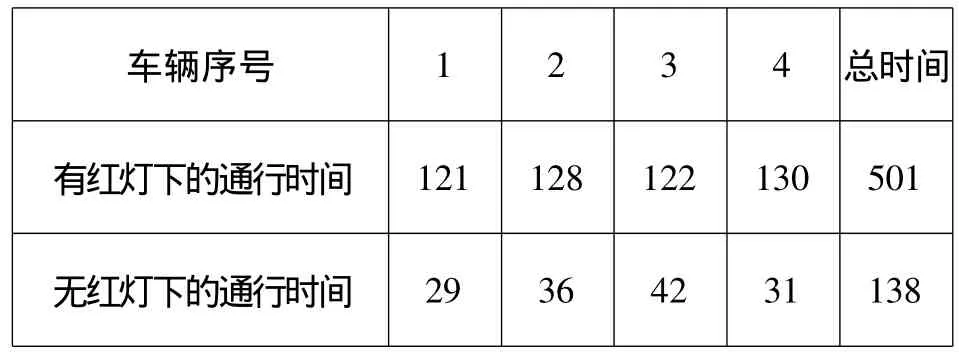
表2 有无红灯下的机动车通行时间

(一)数据计算。机动车道数N=3;车流量λ=281/1800=0．156;平均通行时间 t=(501+138)/8=79．875;通行效率 μ =1/79．875=0．013;交通强度 ρ=/(Nμ)=0．156/(3*0．013)=4 ＞1。

(二)结果评估。通过实验测得的数据结果计算出交通强度大于1，按机动车道模型的指标可以得出在此时间间隔中交通是拥堵的。而在实际测量过程中以行人和驾驶员的经验也认为此时段交通不顺畅。所以模型得出的具体结果与实际相符，可以用来对现有机动车道数是否能使交通顺畅进行评价。

六、改善方法

利用机动车道排队模型可以规划设计未来城市道路的机动车道数量，而因机动车道较少而引起交通拥堵可通过下面三个方法解决:

(一)拓宽马路以增加机动车道数量。在行人与非机动车数量较少的道路上可以适当减少人行道与非机动车道的宽度，增加机动车道数量以缓解交通拥堵的现状。这种方法的优点是成本适中，缺点是作用有限且影响行人与非机动车交通感受。

(二)将机动车道“瘦身”以增加机动车道数量。由于国家政策的变化，目前机动车道标准宽度小于从前，可以在不改变其他设施的情况下减缓拥堵现象。这种方法的优点是成本极低，基本改变其他现状，减少驾驶员插缝隙的习惯也更加安全，缺点是增加的车道数有限且因车型大小道宽的设计需着重考虑。

(三)在车流量较大的地段建设高架。在经济发达的大城市的车流量极大的地段可以建设高架，这也是变相增多机动车道数量以通过分流来减缓交通拥堵。它的优点是高架可以成倍地增加车道数目，特别适合车流量多的中心地带，但缺点也很明显，高架的成本极高，且会在一定程度上改变周围环境。

以上三种方式都可以通过增加机动车道数目达到缓解交通拥堵的目的，它们也有各自的优缺点，在实际问题上需要具体问题具体分析，使改善方案更经济、更合理。

七、结语

本文从满足大型城市交通拥堵的实际情况出发，从另一角度提出利用排队论来规划设计机动车道数量以缓解交通拥堵的想法。通过实践证明，机动车道排队模型可以评价现有机动车道数是否符合机动车流量以优化改善，或者通过机动车流量来设计机动车道数量以使交通畅通。有关部门可以以此作为参考来进行未来道路的规划建设与现有道路改善优化。

［1］孟玉珂．排队论基础及应用［M］．上海:同济大学出版社，1989

［2］刘沃野，吴洪臣，吴振宇．排队论在交通控制中的应用［J］．数理统计与管理，1996，1

［3］张于贤，李娜，肖吉军．基于排队论的生产线量化分析及优化［J］．制造业自动化，2014，7

［4］宋文琪，李启亮，金芳，吕葛，蔡艳英，胡立新，张晓飞．基于排队论的门诊化验服务效率评估与改进［J］．中国医院管理，2014，1

［5］郑华平，何霞．基于排队论的交叉口交通流研究［J］．科技信息，2010，35:377 ～378

［6］孟凡星，邬歆，蔡沁林，张伟．交通路口信号灯控制规则对驾驶员行为决策的影响［J］．中国安全科学学报，2013，23(7):43～48

［7］唐秋生，陆由付．基于多通道排队论的公交站台停车位优化研究［J］．湖南理工学院学报，2013，26(4):18～21

［8］刘维维．高速公路收费站设计中的排队论模型分析［J］．黑龙江交通科技，2013，4:184～185

［9］教材编写组．运筹学［M］．北京:清华大学出版社，2012，第4版