基于直觉模糊距离的大型建设项目政府投资群决策方法研究

庞永师，刘景矿，张 磊，陈 怡

（广州大学工商管理学院，广东 广州，510006）

大型建设项目（Mega Construction Project）通常是指投入金额多、建设规模庞大、对国民经济推动力强的项目，政府部门对于该类项目的建设工作拥有一定决策权和控制权[1-2].不同于一般的政府投资项目，大型建设项目作为一个复杂系统，政府投资决策的科学性和效率决定了投资的成败，对经济和社会效益有深远影响[3].政府投资是指政府作为独立经济主体而参与的投资活动，相应地政府投资的大型建设项目属于公共物品范畴[4].政府投资决策的主要任务是明确政府性资金在投资项目上的应用问题，首先需要决定是否投资，继而明确具体投资地点和投资规模，最后确定投资方式[5].在宏观层面上，政府投资决策体现为政府制定的中长期规划，在全国范围或在某一具体区域内，以推动经济发展为出发点，制定关于全局的和较长时间序列的重大问题决策.在微观层面上，政府投资决策着重于确定项目（项目的审批）和资金注入等相关具体问题.

目前对政府投资决策的研究，大多以经济学的视角针对政府投资的规模、模式、特点和存在的问题而展开，如William Leblanc等人[6]认为政府投资行为影响了资源在当期消费与未来收益的平衡关系；Cavallo Eduardo等人[7]分析了发展中国家政府投资与个人投资的关系；Kappeler Andreas等人[8]研究了欧洲公共投资的组成及决定因素，并着重分析对财政分权的作用；有学者尝试引入行政管理学和法学等思想，从管理和规章制度的角度，以社会效益为目标对政府投资决策的行为进行研究[9]；还有的学者对政府投资项目的管理问题进行了探讨，如陈瑜等人[10]对政府投资的大型复杂项目管理的内容进行了分析，构建了总体项目框架，为从总体把握项目管理内容提供了有益借鉴.上述研究只涉及到政府投资项目决策机制、体制等，而涉及到政府项目投资决策方法的文献研究相对较少，大部分研究集中在多目标决策法、博弃决策分析法、实物期权法、柔性决策法以及决策支持系统等[11-14].将直觉模糊距离法引入政府投资项目的投资决策中，针对专家论证环节，引入该方法将各专家论证意见集结为一致性结果，并且针对多决策主体参与的评估、讨论和听证等环节，采用理性聚类方法集结主体偏好进行投资决策分析，为政府投资决策部门制定科学决策提供参考.

1 大型建设项目政府投资群决策

大型建设项目政府投资决策需要经过专家论证和有公众参与的评估、讨论、听证环节[15].大型建设项目决策的不确定性和复杂性决定了决策过程的复杂程度，为了促进决策向科学化和民主化发展，决策主体的构成必将从以政府为单一投资决策主体向投资决策主体多元化的方向转变.信息、偏好和方案评估能力是衡量决策质量的关键因素，但这些因素与个体的经验和对问题的认知能力密切相关，对于大型建设项目投资这种复杂的决策问题而言，带有多重目标和不确定性等特点，政府（投资主管部门）难以独自完成，需要借助专业人士的知识和能力，如咨询机构和专家，为决策提供科学的支持.因此，在大型建设项目投资决策专家论证环节，群决策主体为专家，包括了政府部门研究机构、高校、建设行业或咨询单位等有专门技能或专业知识的专家.

然而，政府投资项目所带来的社会经济影响与民生有着千丝万缕的联系，为了维护政府的公信力和公众的权益，政府投资决策的制定中必须考虑公众的意见.因此，在大型建设项目投资决策评估、讨论、听证环节，群决策主体为政府相关部门、专家和公众代表.

2 基于直觉模糊距离的政府投资群决策分析

2.1 专家论证环节

2.1.1 相关理论

针对专家对项目建议书的论证环节，由于有多个专家参与决策，会出现专家的评估意见一致和冲突共存的情况，应用直觉模糊距离的方法可将各专家论证意见集结为一致性论证结果，为政府投资决策部门提供参考意见.

设参与决策的专家集为S={s1,s2,…,sm}，可选方案集为 A={a1,a2,…ar}，可选方案的评价指标集为B={b1,b2,…,bn}.

由直觉模糊距离的含义[16-17]，可得

⑴若两位专家之间对方案i的意见完全一致，则二者的直觉模糊距离为0；

(2)若两位专家之间对方案i的意见完全相反，则二者的直觉模糊距离为1；

⑶若两位专家之间对方案i的意见在一定程度上不一致，则二者的直觉模糊距离取[0,1]上的值.

根据实际情况，第k位专家根据自身的经验和偏好对方案i的第 j个评价指标做出的直觉模糊评价为=kkk) ，为可选方案i的第 j个 评价指标真隶属度， fijk为可选方案i的第 j个评价指标假隶属度，=1--，为不确定程度.

则第k位专家对可选方案集A的直觉模糊评价偏好矩阵为

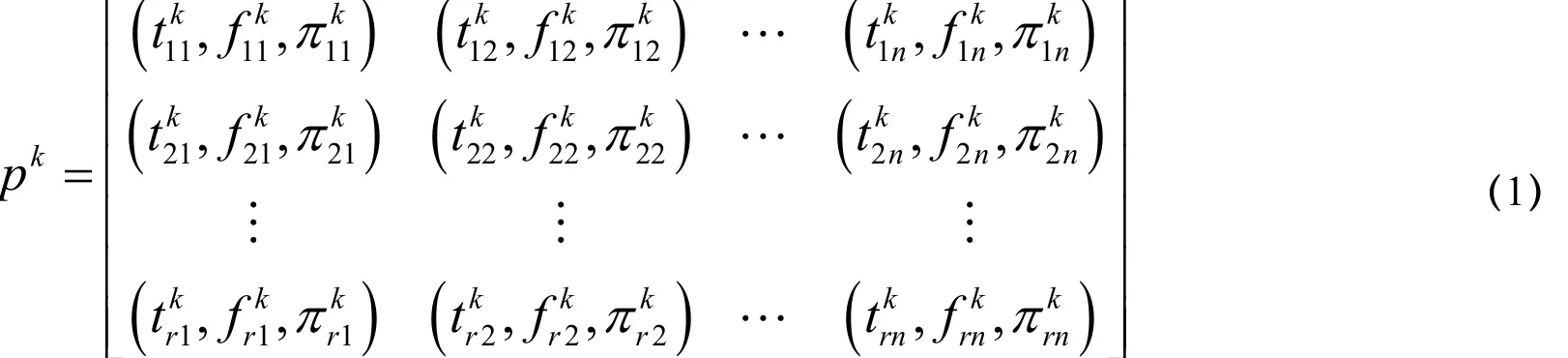
其中：i = 1,2,…,r ；j=1,2,…,n ；k =1 ,2,… ,m .

设评价指{b1,b2,…bn}标的权重分别为w=w2,…,wn），=1.每一对专家（k,u ）对可选方案i的直觉模糊距离为

则有对可选方案i（i=1 ,2,…,r）的意见一致程度矩阵（AQ ），表示m位专家两两对可选方案i论证意见的一致程度，

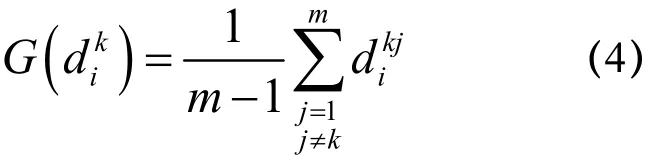
专家k（k= 1,2,…,m）的相对一致程度为

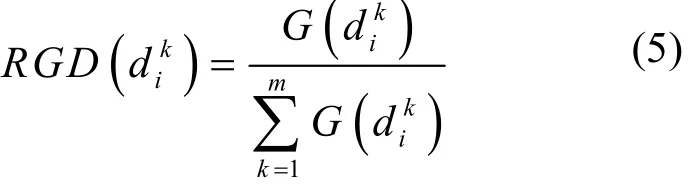
则每位专家的相对重要权重为

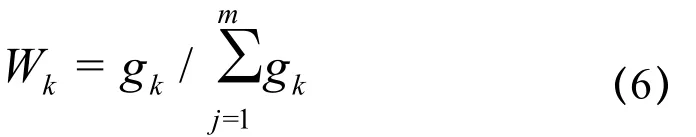
其中： k =1,2,…,m ，集结每位专家的相对重要权重和对可选方案意见的相对一致程度，可得全部专家对可选方案i（i=1 ,2,…,r ）意见的综合一致程度为

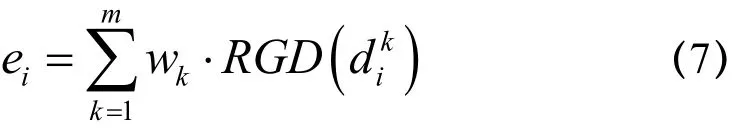
对求得的ie值排序，取值最小的方案表示全体专家对此方案评价的一致性程度最高，专家间的意见分歧最小.

2.1.2 算例

设某大型建设项目专家论证环节，群决策中的专家集 S={s1,s2,…,sm}，备选方案集 A={a1,a2,…ar}，,备选方案的评价准则或指标集为B={b1,b2,…,bn}.

现根据每位专家对备选方案的个人评价意见，对专家群体评价意见的一致度进行分析.并设定评价准则b1，b2，b3的权重分别为w1=0.3，w2=0.5，w3=0.2；专家s1是三位专家中最重要的，则r1=1.专家 s2，s3相对于专家 s1而言的相对权重分别为r2=0.6，r3=0.8.则三位专家1s,2s,3s的相对重要权重分别为1w=0.42，2w=0.25，3w=0.33.根据评价准则或指标，三位专家对备选方案a1、a2的直觉模糊评价偏好矩阵分别为

根据上述每位专家对备选方案的直觉模糊评价偏好矩阵,可分别计算出每一对专家（k, u ）对方案a的直觉模糊距离和:、2

LDH检测：空腹采集患者静脉血，不抗凝，离心分离血清。应用LDH检测试剂盒（成都元和华盛股份有限公司产品）和i2000全自动生化分析仪（美国Abbott Laboratories公司产品）检测LDH。正常值参考范围：150～245 U/L。

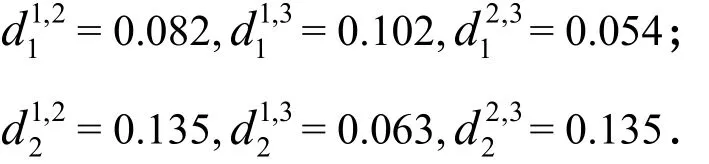
则，3位专家对方案1a,2a的一致度矩阵分别为

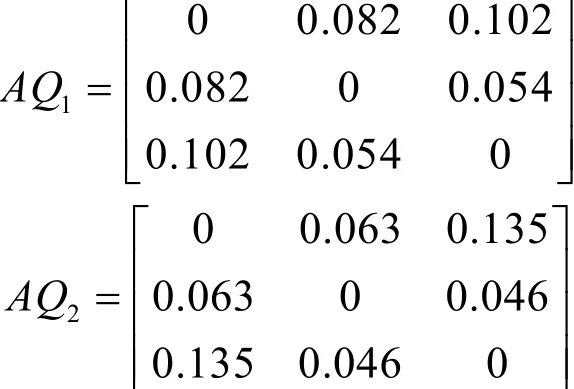
对于方案1a,每位专家的平均一致度分别为

每位专家的相对一致度分别是

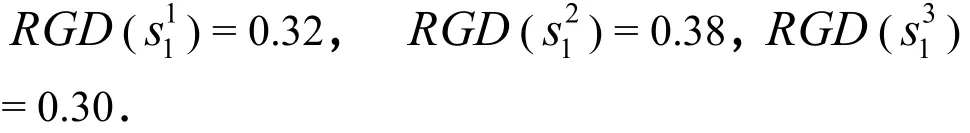
三位专家评价的综合一致度为

按照上述计算步骤,同理可得三位专家对方案a2评价的综合一致度为

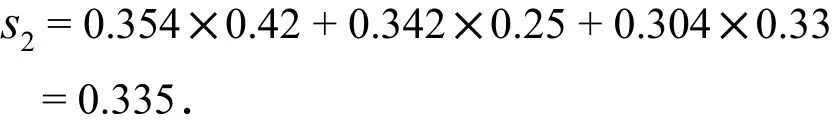
因为1s＜2s,所以专家群体对方案2a的意见一致度要强于方案1a.

2.2 评估、讨论和听证环节

由于大型建设项目对社会和经济有深远的影响，与公众的切身利益密切相关，除了之前的专家论证环节，在正式审批前还应组织听证会，进入评估、讨论、听证环节.该环节的参会者主要由政府相关部门、专家和公众代表组成，政府投资决策部门按听证会最终讨论结果审批项目，并公开发布审批结果.

从理论上讲，政府投资决策部门与社会公众的目标函数应该是统一的，但是在实际大型建设项目投资决策过程中，作为主要决策主体的政府投资决策部门其决策行为不仅受到成本和收益等因素的制约，还受到个体偏好的影响，因此政府投资决策部门与公众的目标函数可能出现不一致的情况.虽然参与评估、讨论和听证等环节的主体有主观和客观层面的差异性，但是可以通过聚类方法，使特定环节的各类主体形成不同的聚类，即使每个聚类中主体的意见有所差异，但大体上是相近的，可以应用理性聚类方法集结决策主体偏好.

2.2.1 相关理论

设某环节的主体成员集Ψ中有 'N个成员，决策方案有M个，每个方案有n个评价指标.令所有主体成员之间进行思维交互，自然分成不同的聚类，使每个聚类产生能够协调成员意见的领导成员，他能将所在聚类的意见协调一致.利用MCDSA算法求得领导成员的数目为N，因此仅需对这N个领导成员进行聚类[17].每个领导成员对M个方案的n个评价指标的评价值为，

其中: t =1,2,…,M,i=1,2,…,N ,j=1,2,…,n,且非负，则评价值矢量=,…,｝是领导成员中第i个成员对第t个方案的偏好.设主体成员集Ψ中各成员偏好互相独立而形成Q个聚类.若表示第t个方案中，第q个聚类中成员个数，则，其中1≤Q≤N，将第q个聚类记为.

设 Cq为各聚类中心点偏好矢量集，则第q个聚类 Rt的偏好是第q个聚类中心点的偏好，即

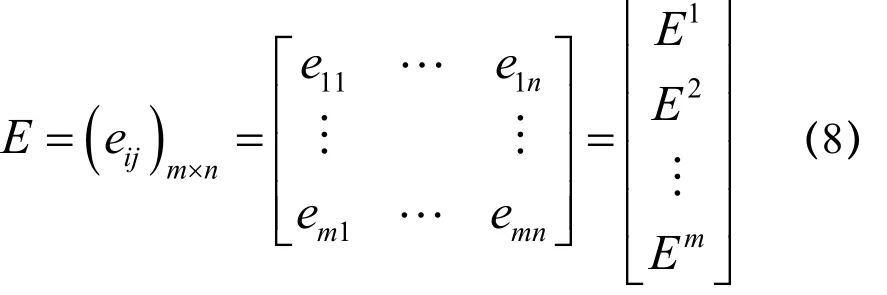
对于M个备选方案和n个评价指标的成员集偏好矩阵 （）nmijeE×= ，设其熵值为

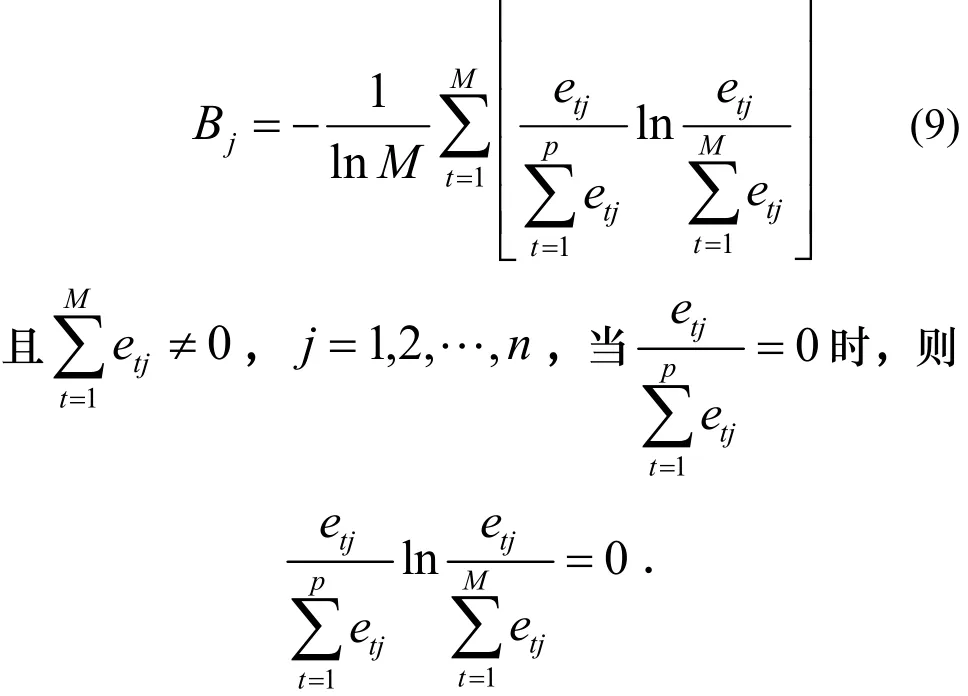
由熵的定义可知，评价指标j的熵越大，则方案在该指标熵取值与该指标最优值越接近，熵权值可定义为

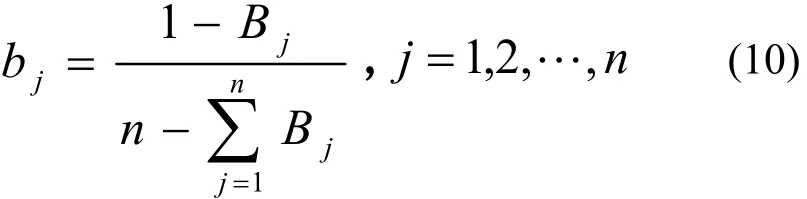
因此，基于成员集Ψ的偏好矩阵的方案评价指标熵权是：

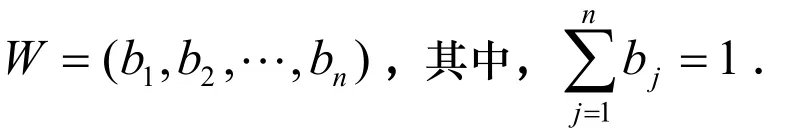
由此可得M个方案的综合评价值矢量为

因此，选择V值最大的方案即为最优的决策方案.

2.2.2 算例

设群体Ψ(指全部参与投资决策群体成员包括政府相关部门、专家和公众代表)中有M 个成员，针对某投资决策问题存在着p个方案,每个成员就n个评判准则对这p个方案进行评价.现有200个成员构成大群体Ψ，该大型建设项目投资决策存在三个方案，分别记为方案 1，方案 2，方案 3,每个成员对该三个方案采用四个评价准则,分别记为准则1，准则2，准则3，准则4.针对方案1,200个成员根据第一阶段的群体思维交互,假设群体中能达成完全一致意见的比例为8%，运用MCDSA算法得到群体领导集Ψ，该领导成员集有 24个成员.Ψ 中的第i个成员利用四个评价准则对方案1进行评价,可得原始评价值为ijx，24个成员可得24×4=96个评价数据.为了消除不同准则的不同量纲的影响，需要对这些数据进行非量纲化处理.借助模糊数学的隶属度函数概念根据数值计算越小越好的特性进行如下标准化处理：

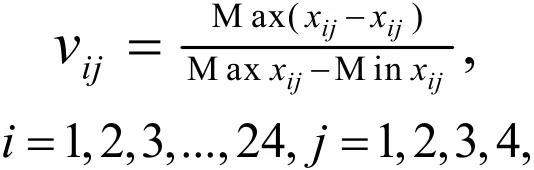
其中：Maxxij，Minxij是针对第j个评价准则的某个成员评价值的最大值和最小值，vij为规范化后的评价值.因此，得到标准化矩阵

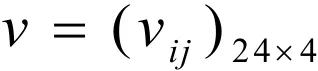
并且0≤ijv，取阀值,75.0=γ，p=q=2，下同，利用式：

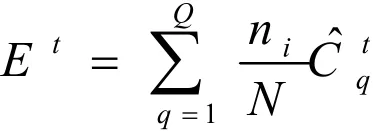
得方案1的群体偏好矢量为

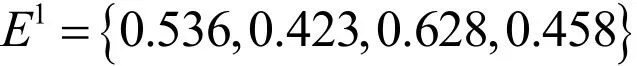
200个成员对方案2进行评价，根据第一阶段的群体思维交互,假设群体中能达成完全一致意见的比例为10%；运用MCDSA算法得到群体领导集Ψ，该领导成员集有20个成员.对所得的数据进行同样的标准化处理,得到标准化矩阵

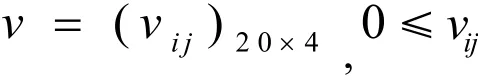
可利用式:

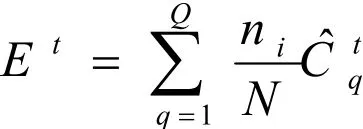
得方案2的群体偏好矢量为：

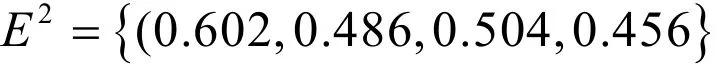
与方案 2类似,针对方案 3，根据第一阶段的群体思维交互，可知群体中能达成完全一致意见的比例为 12%;运用 MCDSA算法得到群体领导集几该领导成员集有18个成员.18个成员对方案3进行评价，对所得的数据进行同样的标准化处理,得到标准化矩阵

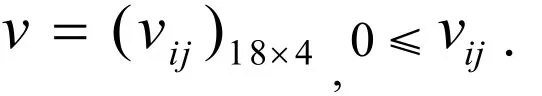
同样利用式

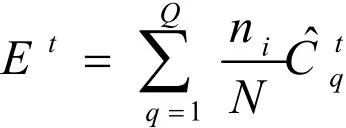
得方案3的群体偏好矢量为

于是得群体偏好矩阵:

将E代入公式(9)-(10)，通过计算得4个评价准则的熵权 W=（0.186,0.248,0.365,0.201），将 E和W带入公式（11）中，可得200个成员针对3个方案的综合评价值矢量：

根据以上计算结果可知,方案1为最优方案.该 方法可以很好地解决多属性群体（决策主体）多方案的大型建设项目投资决策问题,且具备较好的可操作性.

3 结论

大型建设项目政府投资是在市场经济条件下政府供给公共物品、对宏观经济进行调控和推动社会经济健康有序发展的重要手段.其投资结果成败和效率的高低，决定于政府投资决策过程的科学化和民主化程度，需要科学的决策方法来支持.研究成果总结如下：

（1）基于直觉模糊距离理论,提出了在专家论证环节,聚合专家个人意见,同时考虑专家之间的相对重要性，得到专家群体对投资大型建设项目备选方案意见的综合一致度.

（2）针对多决策主体参与的评估、讨论和听证等环节，采用理性聚类方法集结主体偏好做出投资决策，解决在此环节不同主体带来主观和客观层面的差异性问题.

（3）给出了群决策方法的算例，使其方法更具有可操作性，为政府投资决策部门制定科学决策提供参考.

References

[1] BOND S R, MALIK A. Natural resources, export structure, and investment[J]. Oxford Economic Papers, 2009,61(4): 675-702.

[2] DABLA-NORRIS E, BRUMBY J, KYOBE A, et al. Investing in public investment: an index of public investment efficiency[J].Journal of Economic Growth, 2012,17(3):235-266.

[3] SHATREVICH V. Significance of government investment policy in the modern neoclassical economic theory[J].Perspectives ofInnovation in Economics and Business,2009,3(3):38-41.

[4] 谢琳琳.公共投资建设项目决策机制研究[D].重庆：重庆大学，2005.XIE Linlin.Research on the decision—making mechanism of public projects[D].Chongqing: Chongqing Unversity,2005.

[5] 尹琳琳.政府投资项目的投资控制问题研究[D].天津：天津大学，2010.YIN Linlin.A Study of the issues of investment control in government projects[D] .Tianjing： Tianjing Unversity,2010.

[6] LEBLANC W, SNYDER J M. Majority-rule bargaining and the under provision of public investment goods[J].Journal of Public Economics, 2000,75(1): 21-47.

[7] CAVALLO E, DAUDE C. Public investment in developing countries: a blessing or a curse? [J] .Journal of Comparative Economics,2011, 39(1): 65-81.

[8] KAPPELER A, Välilä T. Fiscal federalism and the composition of public investment in Europe[J].European Journal of Political Economy,2008, 24(3): 562-570.

[9] 陈辉华, 王孟钧, 朱慧. 政府投资项目决策体系及运行机制分析[J].科技进步与对策, 2008, 25(10): 87-90.CHEN Huihua,WANG Mengjun,ZHU Hui.Analysis on decision-making system and operational mechanism of the government investment projects[J]. Science & Technology Progress and Policy, 2008, 25(10): 87-90.

[10] 陈瑜, 罗晟, 乐云. 政府投资大型复杂项目总体项目管理框架研究[J].工程管理学报, 2012, 26(5):57-61.CHEN Yu,LUO Sheng,LE Yun. Integration management framework of large complex project funded by government[J].Journal of Engineering Management,2012,26(5):57-61.

[11] 王喜军,王孟钧,陈辉华.政府投资项目决策体系及决策机制分析[J].科技管理研究，2009，(07):107-109.WANG Xijun,WANG Mengjun,CHEN Huihua. Analysis on decision-making system and decision-making mechanism of the government investment projects[J].Science and Technology Research, 2009(07): 107-109.

[12] 李洪江.不确定性投资决策的实物期权方法—项目综合评价、阶段性预算分析与无形资产定价[D].大连：大连理工大学, 2002.LI Hongjiang.Real options approaches for investments under uncertainty—projects appraisal, staged investments analysis&intangible assets pricing[D].Dalian：Dalian University of Technology,2002.

[13] 张婕.基于柔性理论的大型工程投资决策研究[D].南京：河海大学,2007.ZHANG Jie.Researeh on investment decision making for large project based on flexibility theory[D].Nanjing:Hohai University,2007.

[14] 杨亚频.政府投资项目决策系统演化机理及其仿真研究[D].长沙：中南大学，2011.YANG Yaping.Study on government investment decision-making system evolution me-chanism and simulation[D]. Changsha:Central South University,2011.

[15] 夏立明,朱俊文,李丽红.政府投资项目投资决策程序研究[J].天津理工大学学报，2005,21（04）：35-39.XIA Liming, ZHU Junwen, LI Lihong.Study on decision making process for fiscal projects[J].Journal of Tianjin Technology University,2005,21（04）：35-39.

[16] 谭春桥, 张强. 基于直觉模糊距离的群决策专家意见聚合分析[J].数学的实践与认识, 2006, 36(2): 119-124.TAN Chunqiao,ZHANG Qiang. Aggregation of opinion in group decision making based on intuitionistic fuzzy distances[J]. Mathematics in Practice and Theory, 2006,36(2):119-124.

[17] 李鹏.吴君民.朱建军.基于新直觉模糊距离的随机决策方法[J].系统工程理论与实践, 2014,34(06):1517-1524.LI Peng,WU Junmin,ZHU Jianjun.Stochastic multi-criteria decision-making methods based on new intuitionistic fuzzy distance[J].Systems Engineering-Theory &Practice, 2014,34(06):1517-1524.

[18] 刘蓉.基于聚类算法的多属性复杂大群体决策方法研究[D].长沙:中南大学，2006.LIU Rong.Multi-attribute complex huge group-decision methods research basing on clustering algorithm[D].Changsha: Central South University,2006.