Y形高强钢组合偏心支撑框架结构恢复力模型研究
2015-01-23苏明周
连 鸣,苏明周,王 喆
(1.西安建筑科技大学土木工程学院,陕西 西安 710055;2.中国建筑标准设计研究院有限公司,北京 10048)
在动力弹塑性分析中,恢复力模型是结构计算和分析的基础.偏心支撑框架结构兼有中心支撑框架结构的刚度以及钢框架结构的延性,是一种优良的抗震结构体系[1-3],同时,Y形偏心支撑的耗能梁段置于框架梁外,地震作用下耗能梁段的塑性变形竖向分量很小,不会对框架梁及楼板造成严重损坏,震后更易修复.随着生产工艺的提高和钢结构的发展,高强度钢材已在桥梁工程中大量使用[4-5],并逐渐在建筑结构中得到应用[6].
Y形高强钢组合偏心支撑框架结构耗能梁段(或耗能梁段和支撑)采用Q345钢,其余构件采用Q460钢,在地震作用下,耗能梁段充分发展塑性耗散地震能量,框架梁、柱由于采用高强钢,仍处于弹性或部分进入塑性,可以保证达到抗震设防的目标.因此,Y形高强钢组合偏心支撑框架结构对于研究高强钢材的工程应用具有重要意义.目前,本课题组已完成了两个1/2缩尺单层单跨Y形高强钢组合偏心支撑框架结构平面模型抗震性能的拟静力试验研究[7].
虽然国内外学者对偏心支撑结构进行了大量的试验研究[8-12],但对其恢复力模型的研究非常少.根据试验结果,通过理论分析,提出以屈服点和极限点为特征点并考虑刚度退化的双折线恢复力模型,给出了各特征点参数及理论计算公式,并将计算结果与试验结果进行比较以验证其适用性.
1 恢复力模型研究
1.1 骨架曲线的确定
根据文献[7]试验结果,Y形高强钢组合偏心支撑框架结构荷载-位移骨架曲线可采用考虑刚度退化的双线型,分为弹性段和弹塑性段,各阶段内骨架曲线可简化为直线.如图1所示,骨架曲线由坐标零点(O点)、屈服点(Y点)和极限荷载点(U点)间的直线构成.骨架曲线需要确定除零点外的其余两点,即需要确定弹性刚度Ke、屈服位移Δy、屈服荷载 Py、屈服后刚度 Kp、极限位移 Δu、极限荷载Pu.
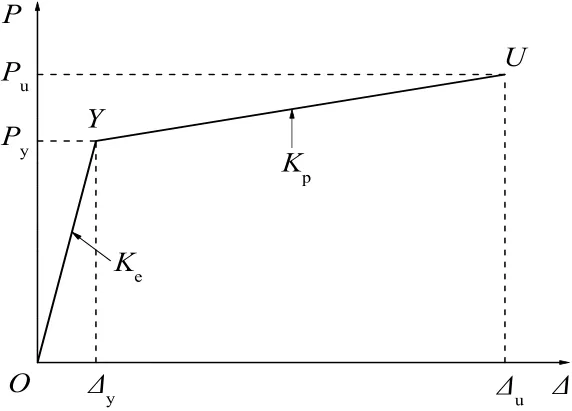
图1 高强钢组合Y形偏心支撑框架的骨架曲线模型Fig.1 The restoring force model of Y-HSS-EBF
1.1.1 弹性刚度
弹性刚度为屈服荷载 Py与屈服位移 Δy的比值.基于Y形高强钢组合偏心支撑框架结构的受力特点,其水平抗侧刚度可由图2所示的简化模型进行分析.则结构的水平抗侧刚度Ke为

其中:K1为框架的抗侧刚度,K2为支撑对结构提供的刚度,K3为耗能梁段的抗剪刚度,K4为耗能梁段-框架梁节点区域框架梁的抗剪刚度.
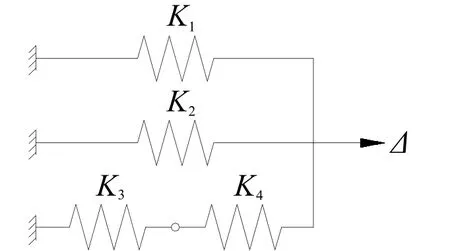
图2 简化分析模型Fig.2 Equivalent spring model for Y-HSS-EBF
由于Y形高强钢组合偏心支撑框架结构的框架梁、柱采用高强钢,当耗能梁段进入屈服时,框架梁、柱仍处于弹性,故结合该结构形式的特点,可由弹性分析可以得到框架的抗侧刚度K1计算公式:

式中:E为弹性模量,Ib和Ic分别为框架梁、柱的截面惯性矩,lb和lc分别为框架梁、柱的长度.
计算支撑对结构提供的刚度K2时,根据Y形偏心支撑框架结构中支撑的受力特点,假定支撑为悬臂梁,由弹性分析可得:

式中:E为弹性模量,I为支撑的截面惯性矩,α为支撑与框架柱的夹角,lbr为支撑长度.
耗能梁段及其与框架梁节点区域的受力如图 3所示.耗能梁段屈服时的抗剪刚度K3以及耗能梁段-框架梁节点处框架梁的抗剪刚度K4可由式(3)和式(4)计算得到:

其中:h0,L和 tw,L分别为耗能梁段腹板的高度和厚度,h0,b和tw,b分别为框架梁的腹板高度和厚度,G为剪切模量,e为耗能梁段长度,lb为框架梁长度.

图3 耗能梁段及其与框架梁连接区域受力Fig.3 Load conditions of the connection between link to beams
将式(2)-(5)带入式(1)即可得到 Y-HSS-EBF的弹性刚度Ke的计算公式:

1.1.2 屈服位移
如图4所示,Y形高强钢组合偏心支撑框架结构的屈服位移Δy由三部分组成,即:

其中:Δ1为支撑轴向变形产生的位移,Δ2为耗能梁段剪切变形产生的位移,Δ3为耗能梁段弯曲变形产生的位移.

图4 Y形偏心支撑框架层间侧移组成Fig.4 Components of story displacement for Y-EBF
根据偏心支撑结构的设计方法,支撑按轴心压杆进行设计,由胡克定律可知,当耗能梁段达到屈服时,支撑轴向变形产生的位移为

其中:Nd为支撑轴力,ld为支撑长度,E为弹性模量,Ad为支撑截面面积.根据小变形假定,由支撑轴向变形产生的框架侧移Δ1为

式中:θ为支撑与框架梁的夹角,fy,br为支撑钢材的屈服强度,lbr为支撑的长度,L为跨度.
Y形偏心支撑框架结构屈服时,耗能梁段进入塑性,由耗能梁段剪切变形产生的框架侧移Δ2与耗能梁段的剪切转角γv具有如下关系:

其中:e为耗能梁段长度.γv表达式为
其中:VL为耗能梁段剪力,AL为耗能梁段截面面积,G为剪切模量,则有

式中:fy,L为耗能梁段的屈服强度.耗能梁段由弯曲变形产生的轴向应变为

根据几何关系,耗能梁段弯曲变形产生的框架位移为

将式(9)、式(12)、式(14)代入式(7),整理得:

1.1.3 屈服荷载
荷载达到屈服值之前,假定偏心支撑框架结构基本上处于弹性阶段,忽略侧向位移产生的二阶效应,则屈服荷载为

其中:Ke为弹性刚度,由式(6)计算得到,Δy为屈服位移,由式(15)计算得到.
1.1.4 极限荷载
根据偏心支撑框架结构的设计理念、设计方法以及试验结果,Y形高强钢组合偏心支撑框架结构理想的的受力机理为:在水平力作用下,耗能梁段首先进入塑性,并且通过其塑性变形耗散地震能量,当耗能梁段达到极限状态时,由于支撑采用高强钢,其虽出现变形但仍处于弹性并且不发生屈曲,而柱脚和框架梁两端进入全截面屈服形成塑性铰,此时结构达到极限状态,典型的屈服机制如图5所示.根据结构的屈服机制,其极限承载力可根据虚功原理进行求解.假定结构达到极限状态时,耗能梁段达到全截面塑性、柱脚和框架梁两端进入全截面屈服,偏心支撑框架结构的内力虚功和外力虚功分别为

图5 Y-HSS-EBF极限状态下的变形Fig.5 Mechanism typology for Y-HSS-EBF

其中:ML、VL分别为耗能梁段端弯矩和剪力,γp、δp分别为耗能梁段极限状态时的塑性转角和剪切变形,Mbp、Mcp分别为框架梁、柱的塑性抗弯承载力,θ为框架侧移角,h为层高,V为水平力.
由内力虚功和外力虚功相等,得到水平力V为

耗能梁段截面上既有正应力σ和剪应力τ时,屈服准则为:σ2+3τ2=fy2=3fvy2,则有

由上式可得到耗能梁段弯矩和剪力的相关关系式:

式中:Mp和 Vp分别为耗能梁段的截面塑性抗弯和抗剪承载力.VL、ML可有下式确定[13]:


式中:0.08为 AISC341-10[13]规定的剪切屈服型耗能梁段塑性转角限值,KV、KM分别为耗能梁段屈服后的抗剪刚度和抗弯刚度,可由下式计算:

式(20)分别对ML、VL求偏导可得:

其中:ξ为控制塑性变形的系数[14].式(26)、(27)消去ξ,即:

由小变形假定并忽略框架梁的轴向压缩变形,根据屈服机制有

将式(26)、(27)、(28)代入上式,可解得:

将式(22)、(23)、(30)、(31)代入式(19)即可得到极限荷载.
1.1.5 极限位移
根据 AISC341-10规定的耗能梁段弹塑性转角限值和《建筑抗震设计规范》(GB50011-2010)[15]弹塑性层间侧移限值的规定,Y形高强钢组合偏心支撑框架结构理想的屈服机制为当耗能梁段转角达到限值时,结构整体形成延性破坏机构,计算结构极限位移时假定其破坏为理想的屈服机制.
由于耗能梁段转动产生的框架侧移远大于其端部剪切变形对框架侧移的贡献,因此在估计结构极限位移时只考虑耗能梁段转动产生的框架侧移.由小变形假定,并忽略框架梁的轴向压缩变形,有

式中:Δu为结构的极限位移,θp为柱脚的极限转角,h为层高,γe,L和γp,L分别为耗能梁段的弹性转角和塑性转角,e为耗能梁段长度.由Δy=γe,Le可得:

其中:Δy由式(15)确定.同时,γp,L可取AISC341-10规定的剪切屈服型耗能梁段塑性转角限值0.08rad,则结构极限位移为:

同时,当 eVp/Mp≤1.04时,Q345钢剪切屈服型耗能梁段的最大塑性转角可比规范限值提高25%[16].
1.1.6 屈服后刚度
屈服后刚度Kp可由下式计算:

式中:Py和Pu分别为结构的屈服荷载和极限荷载,Δy和Δu分别为结构的屈服位移和极限位移.
1.2 滞回规律
图6为剪切屈服型Y形高强钢组合偏心支撑框架结构的双折线恢复力模型,其滞回规律如下:
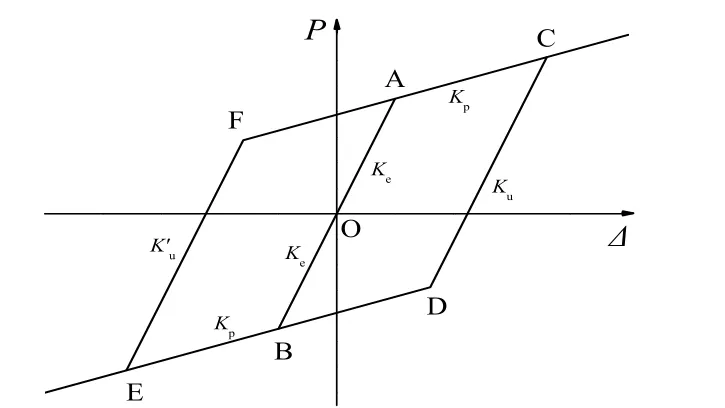
图6 恢复力模型Fig. 6 The restoring force model
(1) 在屈服点之前,结构处于弹性阶段,结构加载和卸载沿骨架曲线弹性段(OA段和OB段)进行,加载刚度和卸载刚度均为Ke.
(2) 在屈服点之后,结构进入弹塑性阶段,加载路径沿骨架曲线进行(AC段),卸载时直接指向反向屈服点D,卸载刚度为 Ku,到达D点后沿骨架曲线进行反向加载(DB、BE段).在此阶段,反向卸载及正向再加载时直接指向正向屈服点F,卸载刚度为 Ku’此后沿骨架曲线进行加载,开始下一级位移控制的荷载循环.如图7和图8所示,正、反向卸载刚度通过文献[7]试验数据回归分析后得到:


图7 正向卸载刚度退化拟合Fig. 7 Regression reloading rigidity of positive direction

图8 反向卸载刚度退化拟合Fig.8 Regression reloading rigidity of opposite direction
2 建议的恢复力模型与试验结果比较
图9和图10分别给出了文献[9]中耗能梁段长度为300 mm的试件(Y-1)和耗能梁段长度为500 mm的试件(Y-2)由本文方法计算得到的骨架曲线、滞回曲线与试验结果的比较.

图9 计算曲线与试验骨架曲线的对比Fig.9 Comparisons of calculated skeleton curves and test ones

图10 计算曲线与试验滞回曲线的对比Fig. 10 Comparisons of calculated hysteretic curves and test ones
从图中可以看出,计算骨架曲线弹性刚度和极限荷载略大于试验曲线,由于是简化分析,因此试件进入弹塑性状态之后两曲线略有不同,但总体上讲,计算骨架曲线与试验曲线的吻合较好,并且计算曲线整体趋势与试验曲线大致相同,各阶段的位移和加、卸载刚度与试验较为接近.
试件骨架曲线特征点理论计算结果和试验结果的比较如表1所示,各试件特征点理论计算值与试验值较为接近,除试件Y-2极限位移误差为11 %外,其余参数误差均在10 %以内,说明理论计算公式具有一定的精确性.因此,本文建议的恢复力模型可以为剪切屈服型 Y形高强钢组合偏心支撑框架结构的抗震性能评估和动力弹塑性分析提供依据,具有一定的参考价值.

表1 骨架曲线特征点理论计算结果与试验结果的比较Tab.1 Calculated characteristic points of skeleton curves and test results
3 结论
基于 Y形高强钢组合偏心支撑框架结构试验曲线,建立了适于剪切屈服型Y形高强钢组合偏心支撑框架结构并且考虑刚度退化的双折线恢复力模型.通过理论分析并且基于试验数据,给出了各特征点参数、各阶段刚度计算公式以及恢复力模型的滞回规律.由本文提出的恢复力模型计算所得曲线与试验曲线较为接近,可以为剪切屈服型Y形高强钢组合偏心支撑框架结构的抗震性能评估和动力弹塑性分析提供参考.
References
[1] ROEDER C W, POPOV E P. Eccentrically braced steel frames for earthquake [J]. Journal of Structural Division,1978, 104(3): 391-412.
[2] JAIN A K, GOEL S C. Seismic response of eccentrically braced frames [J]. Journal of the Structural Division,1980, 106(4): 843-860.
[3] BOSCO M, ROSSI P P. Seismic behaviour of eccentrically braced frames [J]. Engineering Structures,2009, 31: 664-674.
[4] MIKI C, HOMMA K, TOMINAGA T. High strength and high performance steels and their use in bridge structures[J]. Journal of Constructional Steel Research, 2002,58: 3-20.
[5] AZIZINAMINI A, BARTH K, DEXTER R, et al. High performance steel: research front—historical account of research activities [J]. Journal of bridge engineering,2004, 9(3): 212-217.
[6] 施刚, 石永久, 王元清. 超高强度钢材钢结构的工程应用[J]. 建筑钢结构进展, 2008, 10(4): 32-38.SHI Gang, SHI Yongjiu, WANG Yuanqing. Engineering application of ultra-high strength steel structures [J]. Progress in Steel Building Structures, 2008, 10(4): 32-38.
[7] 段留省, 苏明周, 焦培培, 等. 高强钢组合Y形偏心支撑钢框架抗震性能试验研究[J]. 建筑结构学报, 2014,35(12): 89-96.DUAN Liusheng, SU Mingzhou, JIAO Peipei, et al. Experimental study on seismic behavior of high strength steel composite K-type eccentrically braced frames [J].Journal of Building Structures, 2014, 35 (7): 89-96.
[8] FOUTCH D A. Seismic behavior of eccentrically braced steel building [J]. Journal of Structural Engineering,1989, 115(8): 1857-1876
[9] PERERAL R, GOMEZ S, ALARCON E. Experimental and analytical study of masonry infill reinforced concrete frames retrofitted with steel braces [J]. Journal of structural engineering, 2004, 130(12): 2032-2039.
[10] MAZZOLANI F M, CORTE G D, ANIELLO M D. Experimental analysis of steel dissipative bracing system for seismic upgrading [J]. Journal of civil engineering and management, 2009, 15(1): 7-19.
[11] BAHRAMPOOR H, SABOURI-GHOMI S. Effect of easy-going steel concept on the behavior of diagonal eccentrically braced frames [J]. International Journal of Civil Engineering, 2010, 8(3): 242-255.
[12] 于安林, 赵宝成, 李仁达, 等. K形和Y形偏心支撑钢框架滞回性能试验研究[J]. 建筑结构, 2010, 40(4): 9-12.YU Anlin, ZHAO Baocheng, LI Renda, et al. Experimental study on hysteretic behavior of K and Y-eccentrically braced steel frames [J]. Building Structure, 2010, 40(4): 9-12.
[13] AISC341-10 Seismic provision for structure steel buildings [S]. Chicago: American Institute of Steel Construction, 2010.
[14] MASTRANDREA L, PILUSO V. Plastic design of eccentrically braced frames, I: Moment shear interaction[J]. Journal of Constructional Steel Research, 2009, 65:1007-1014.
[15] GB50011-2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB50011-2010 Code for seismic design of buildings [S].Beijing: China Architecture Industry Press, 2010
[16] OKAZAKI T, ENGELHARDT M D. Cyclic loading behavior of EBF links constructed of ASTM A992 steel[J]. Journal of Constructional Steel Research, 2007,63(6): 751-765.
