基于坍落度的充填膏体流变特性研究

赵建会，刘 浪

（ 西安科技大学能源学院，陕西 西安 710054）

传统的普通尾砂胶结充填技术在矿山的应用，促进了充填技术的发展[1]．但随着这项技术的发展也暴露出一系列的突出问题[2-3]：充填体强度低、养护周期长、充填效率低、井下脱水污染环境、尾砂利用率低及充填成本高等．为克服以上充填缺陷，唯有提高充填料浆浓度，由此，提出采用膏体充填技术．膏体充填[4]是指把物料制作成“无临界流速、少/无需脱水”的膏状浆体，通过高密度固体充填泵与自重作用，经过管道泵送至井下工作面，进行适时充填采空区的方法．膏体充填主要特点表现为：充填料浆不离析、不沉淀，且采场脱水量少、甚至不脱水，充填体强度增长迅速，充填质量好、效率高、成本低，改善井下作业环境等，膏体充填是近年来充填采矿法的主要研究方向，也是倡导创建绿色矿山的必然趋势．

为了精确定义充填膏体的流变特性，必须测定剪切屈服应力和粘度[5]．屈服应力定义为膏体流动所需的最小应力，关于该屈服应力存在与否还没有统一的结论．但从流变理论可以看出，膏体的屈服应力客观存在，并且对于研究充填膏体流动性非常有意义．充填膏体在受到外部剪切力作用时发生变形（流动），内部相应要产生对变形的抵抗，并以内摩擦的形式表现出来．所有流体在有相对运动时都要产生内摩擦力，这是流体的一种固有物理属性，称为流体的粘滞性或粘性．在充填实践中，通常采用测定坍落度的方式来衡量充填膏体的流变特性．坍落高度，取决于材料屈服应力和密度，而这两者反过来又依赖于化学组成、颗粒比重和粒度等．关于坍落度与膏体剪切应力和粘度的研究由来已久．Tattersall[6]等人最早进行坍落度与膏体流变参数相关性研究，但是得出的结论是无关性； Murata[7]等人从理论的分析了坍落度与剪切应力、粘度的关系，并引入圆柱坍落筒进行坍落度实验，最终得出坍落度与屈服应力相关，同时验证了坍落度与膏体粘度无关；Christensen[8]等人发现以往研究的不足，并从无量纲的角度建立坍落度与膏体屈服应力的相关性模型，该模型与料浆的物理属性及坍落筒的形状无关；Pashias[9]等人建立无量纲模型，并应用不同的膏体进行实验，最终使理论预测模型和试验结果基本一致．

结合矿山膏体充填实践，从坍落度的角度来研究充填膏体流变特性，并构建相应的理论模型．同时，配制不同灰砂比与不同浓度的充填膏体，验证坍落度与膏体屈服应力的相关性，进一步确定所建模型的准确性，以期为矿山提供一个简单、易于现场应用的充填膏体流变参数的测定方法．

2 充填膏体流变学原理

充填膏体作为一种流体，在受到外部剪切力作用时发生流动变形，内部相应产生对变形的抵抗，并以内摩擦的形式表现出来．这是流体的一种固有物理属性，称之为粘滞性或粘性．根据不同的流变性能，可将流体分为牛顿流体和非牛顿流体．各类典型的流变模型，见表1．

注：Power Equation 模型中，当n=1时，为牛顿流体；当n＞1时，为剪切稠化；当n＜1时，为剪切稀化．

在长期的充填实践和科研工作中，普遍认为充填膏体流变特性符合宾汉模型（或者），利用屈服应力和粘度两个参数来表征料浆的流变特性，其流变模型为：

式中：σ为应力；0σ为屈服应力；η为粘度；γ为应变速率；t为时间．

由公式（1）可知屈服应力0σ和粘度η是反映充填料浆流变的两个主要参数，当σ＜0σ时，表现为固态，膏体不发生流动变形；当σ＞0σ时，充填体结构发生破坏，进入液体状态，并作为牛顿体流动；当外力降低至屈服应力以下时，该膏体又重新固化．

3 基于坍落度充填膏体流变参数测算

坍落度是高浓度充填研究中从混凝土借用的一个概念[10]，主要表征高浓度充填料浆流动性能，坍落度试验步骤如图1所示．坍落度高低直接反映了高浓度料浆的流动状态和摩擦阻力大小．经研究证实，坍落度值主要取决于料浆中固体颗粒的级配和料浆浓度．它的力学含意是料浆因自重而流动、因内部阻力而停止的最终变形量．它的大小直接反映着料浆流动性的好坏与流动阻力的大小：坍落度值越大，料浆流动性能越好，料浆流动阻力越小．

图1 坍落度试验步骤Fig.1 The procedure of slump test

3.1 坍落度–圆锥坍落筒模型

圆锥坍落度的测试方法：用一个上口100 mm、下口200 mm、高300 mm的锥状坍落筒（形状与尺寸见图2），具体坍落度的测定方法应参考《普通混凝土拌合物性能试验方法》（GBJ8-85）的规定．试验时先润湿坍落筒，并把它放在一块刚性的、平坦的、湿润且不吸水的底板上（水磨石地面），然后用脚踩两个脚踏板，使坍落筒在装料时固定位置，充填膏体料浆装入筒中．由于试验的充填料浆流动性好，试验时尾砂充填料浆一次装满，然后用直径20 mm的钢棒捣实，否则充填料必须分三层装入，用捣棒捣实，每层捣实后的高度大致为坍落筒高的三分之一；料浆装满筒后，刮平桶口，刮清桶底部周围，然后小心地垂直提起坍落筒；待尾砂充填料浆下落平稳后，立即量测筒高与充填料浆试体最高点之间的高差，即为坍落度．

图2 ASTM锥形坍落度实验装置Fig.2 Experimental facility of ASTM cone slump test

由图3可知，在坍落筒中任一水平位置的应力为

其中：zW 为距离筒顶z处以上料浆质量，mg；1r为椎体上半径，m；2r为椎体下半径，m；zr为距离筒顶z处半径，m；H为为椎型坍落筒高度，m．

根据图3可知，zV 的体积即为直线0≤y≤f(x)，0≤x≤z（f(x)在 [0, z]上连续）绕x轴旋转一周所围成的旋转体体积，即：

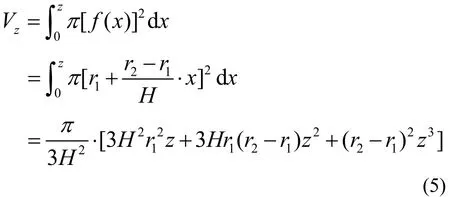
将公式（3）、（4）和（5）代入公式（2）可知，椎型坍落筒任何位置z处应力zP为

图3 坍落筒模型Fig.3 The cone model used for slump test

根据特雷斯卡准则(Tresca Criteria)可知，最大剪应力发生在α=π/4的斜面上，且最大剪应力在数值上等于最大正应力的二分之一．

由此可得：

无量纲化后为：

查阅相关文献[10-12]，假定充填膏体为不可压缩的，则距离坍落筒顶部z处，在坍落筒提起前后zd的体积将不变，如图4所示．

图4 坍落筒提起前后厚度为dz浆体变化Fig.4 The thickness changes between original height and after lifted

同时，可得：

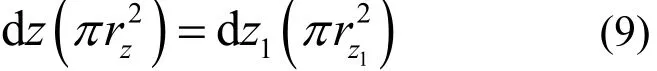
公式（9）可变换为：

根据图4和图5可知，坍落筒提起后，变形1h，是由 zd积分而成，故有：

将公式（10）代入公式（11）可得：

假定坍落筒内充填浆体各层之间没有流动，且不会因为自重而压缩．所以，在1h的区域内，任一截面上应力从上而下增加，直至数值上等于屈服应力．这种关系可以表达为：

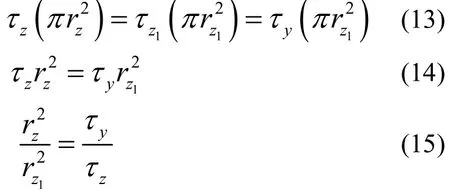
将公式（15）代入到公式（11），可得：

联立公式（16）和公式（7），可得：

由图2可知，r1=0.05 m，r2=0.1 m，H=0.3 m，将其代入公式（17），并求解可得：

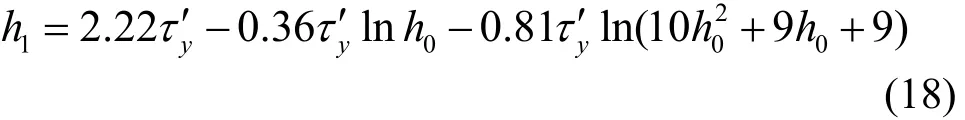
图5 坍落筒提起后应力分布图Fig.5 The stress distribution of the backfill paste after container being lifted

根据图5所示，坍落度是坍落筒提起前后的高度差．可以表示为：

无量纲化后的坍落度可以表示为：

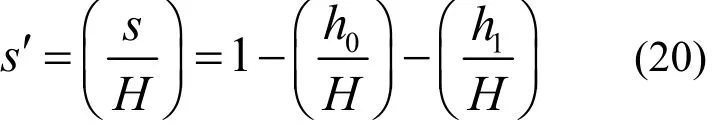
如图5所示，剪切应力在0h处的应力等于充填材料的屈服应力．根据公式（8），无量纲化后的屈服应力表示为：

联立公式（18）、公式（20）和公式（21）可以得出无量纲化后的锥形坍落度与膏体屈服应力的关系式．

3.2 坍落度—圆柱坍落筒模型

圆柱坍落筒可视为锥形坍落筒的特殊情况，其实验装置如图6所示．

图6 圆柱坍落度试验装置Fig.6 Experimental facility of cylinder slump test

如图7所示，对于该坍落筒，任一距离端口z处的压力为

假设充填体为塑性材料，则最大剪切应力为该处应力的一半，可以表达为

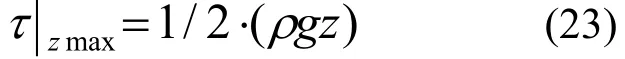
无量纲化后为

由公式（24）可知，该坍落筒上应力沿轴向线性分布，从端口0到底部最大值．沿坍落筒轴向，应力不断增大，在任一位置 h0′处，当该处由于自重引起的应力小于膏体屈服应力，则充填材料保持原状；当该处自重引起的应力大于膏体屈服应力，则充填膏体发生坍落．

在充填过程中，假设该坍落筒实验后，变形区和未变形去的分界线为上下水平移动，所以坍落筒最后实验高度分为：未变形区高度 h0和变形区高度h1，故有：

由公式（12）至公式（19），可得：

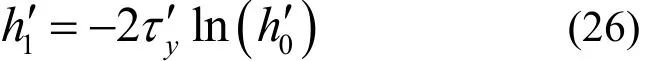
图7 圆柱坍落筒提起后应力分布Fig.7 Stress distribution after cylinder lifting

同理，联立公式（20）、公式（25）和公式（26）可以得出无量纲化后的柱形坍落度与膏体屈服应力的关系式．

4 试验材料及装置

4.1 试验材料物理与化学特性

充填材料基础参数主要包括尾砂的物理特性（容重、密度、孔隙率等）、化学特性（化学组成分析）、尾砂粒级组成等．实验过程中，选用铁矿的尾砂，并取自地表尾矿库总进料口的尾砂浆，经澄清后去除上部清水，然后在阳光下曝晒至含水约15 %，用塑料袋密封包装，运送至实验室进行试验．

表2 尾砂基础物理参数表Tab.2 Basic physical parameters of tailings

表3 尾砂化学元素及其氧化物分析结果Tab.3 Basic physical parameters of tailings

从表3中可以看出，尾砂中金属元素及其氧化物Fe、Al2O3、CaO、MgO含量较高，分别为7.85 %、5.95 %、3.78 %、4.08 %，其他金属元素含量较低．尾砂中非金属元素及其氧化物主要有SiO2、S、P，含量分别为65.96 %、0.11 %、0.07 %，尾砂中硫及硫化物和磷及磷化物含量较低，对充填体影响较小．

图8尾砂XRD衍射图谱Fig.8 XRD diffraction pattern of tailings

图8 为实验铁矿充填用尾砂XRD衍射图谱，从图中可以看出该尾砂的矿物组成以石英为主，这说明表3中铁矿尾矿的主要成分SiO2以石英形式存在，属于高硅型铁尾矿，此外还含一定量的云母和少量的赤铁矿．通过 XRD衍射物相分析出矿物石英、云母和赤铁矿的主要化学成分为SiO2、Al2O3、Fe2O3和K2O，此分析结果与表3化学元素分析结果相吻合．

图9 全尾砂粒度分布曲线Fig.9 The curve of full tailing distribution

从图9中可看出，尾砂d10为1.332 μm，d50为16.752 μm，d90为124.576 μm．尾砂粒级组成不均匀系数为3.68，通常适用于充填的尾砂颗粒的最佳级配应符合塔博方程，一般应介于4～6之间．

4.2 试验装置

测定充填膏体屈服应力与粘度，使用流变仪进行测量，其装置及原理如图10、图11所示．试验过程中选用锥形坍落筒与圆柱坍落筒进行坍落度测试，其具体尺寸与材料如表3所示，两种坍落筒外观如图2、图5所示．

图10 屈服应力与粘度测定装置Fig.10 Yield stress and viscosity measuring device

图11 流变仪测试原理Fig.11 The test philosophy of rheometer

5 试验结果及讨论

5.1 屈服应力与坍落度关系

以铁矿尾砂为例，其物性参数和化学组成见表2、表3．利用所建立的基于锥形与柱形坍落度的膏体充填料浆流变参数测算模型，对比流变仪测定的屈服应力，无量纲后的坍落度与无量纲的屈服应力关系，如图 12、图13所示．当无量纲坍落度为 1时，充填膏体没有坍落（似固体状）；当无量纲坍落度为0时，充填膏体将全部坍落（似液体状）．

通过对比图12与图13可知，当无量纲屈服应力在0～0.1区间内（或者无量纲坍落度大于0.45）时，即屈服应力较小、坍落度较大，利用锥形坍落度实验和柱形坍落度实验测量数据基本与各自模型基本吻合；当屈服应力增大、坍落度变小时，锥形坍落度实验数据与模型逐渐偏离，而柱形坍落度实验数据和模型基本一致．由以上分析可知：当屈服应力较大，坍落度较小时，更适于利用柱形坍落筒．故在充填膏体进行坍落度试验时，选择柱形坍落筒比较适合．

图12 柱形坍落度模型与实验数据对比Fig.12 The comparison of cylindrical slump model and experimental

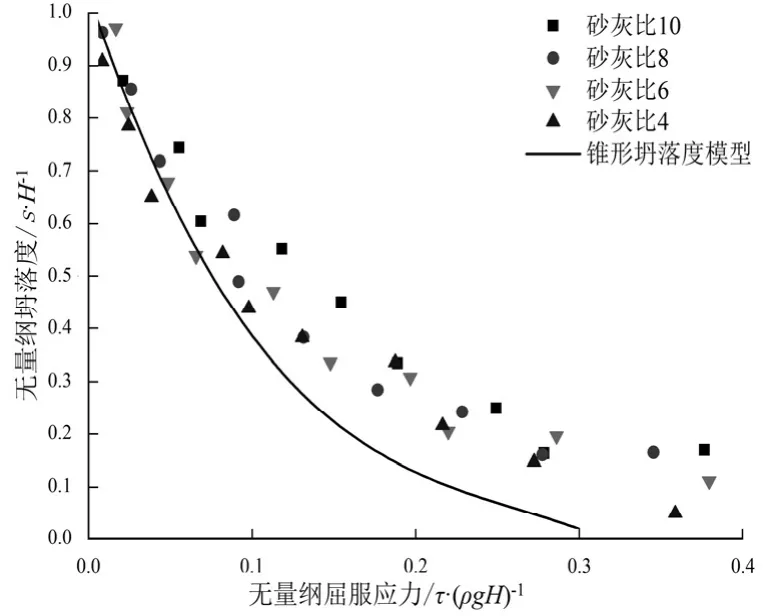
图13 锥形坍落度模型与实验数据对比Fig.13 The comparison of cone slump model and experimental

5.2 膏体屈服应力与浓度的关系

在地表按照一定的砂灰比制备充填膏体，当膏体屈服应力过大，则易于堵塞充填管道，无法进行输送；相反，当膏体屈服应力过小，将无法满足充填强度要求，同时，这将势必降低充填过程中尾砂的使用量．因此，控制充填膏体合理浓度，对于膏体充填实践至关重要．为能够最大限度的利用尾砂和降低水泥使用量，在膏体充填系统中不断提高膏体浓度，达到75 %～85 %，膏体屈服应力与浓度的关系如图14所示．

图14 充填膏体屈服应力与浓度关系Fig.14 The relationship between yield stress and concentration of backfill paste

由图 14可知，充填膏体屈服应力随着浓度增加，且当浓度相同时，随着砂灰比增加屈服应力降低．同时，由图 13可以看出，当充填膏体浓度在75 %～85 %时，充填膏体的屈服应力在200 Pa左右，基本符合以屈服应力200±25 Pa作为充填膏体界定点[13]．

5.3 膏体流变参数与剪切速率的关系

利用流变仪测定充填膏体的流变参数（屈服应力、粘度）过程中，流变参数与剪切速率符合图15中的规律（以浓度为80 %、砂灰比为6的充填膏体为例）．

图15 充填膏体流变参数与剪切速率的关系（以浓度为80%、砂灰比为6的充填膏体示意）Fig.15 The relationship between rheological parameter and shear rate of backfill paste (Taking the paste of concentration: 80%, sand-cement ratio: 6 as example)

同时，由图14可以得出：①充填膏体在测定屈服应力和粘度开始时，屈服应力和粘度迅速增大，随着时间增加回落到某一值时，基本保持不变，稳定后的值是所需要测定的屈服应力和粘度；②当浓度相同，而砂灰比不同时，随着砂灰比增大充填膏体的屈服应力和粘度降低，主要原因是当增大砂灰比，意味着水泥的质量浓度降低，从而降低了充填膏体的粘结力，进而降低充填膏体抵抗变形的能力，所以最终导致充填膏体的屈服应力和粘度降低；③当砂灰比相同，而浓度不同时，随着膏体浓度的增加充填膏体的屈服应力和粘度增加．很显然，增加膏体浓度有利于增加充填膏体的屈服应力和粘度，当砂灰比不变而增大膏体浓度时，水泥的含量也增加，更有利于充填膏体的胶凝和固化，进而增加充填膏体的强度．

6 结论

（1）与锥形坍落度试验相比，柱形坍落度实验与模型更能准确测定高浓度充填膏体的流变参数．同时，柱形坍落度模型在数学公式表现形式上，比锥形坍落度模型更为简单，这个特点对于一些数学基础较弱的矿山工作者尤为重要；

（2）由于锥形坍落筒几何结构较柱形坍落筒更为复杂，难于填料，并且会在填料过程中形成许多气泡，这将势必影响坍落度实验结果．应用锥形坍落筒做实验时，坍落的膏体坍落后的形状不连续，尤其是做高屈服应力的膏体坍落度实验时明显；

（3）柱形坍落筒的设计与制备比锥形坍落筒更为简单，取材方便，圆柱坍落筒可以选择一个任意的圆柱空心管，而锥形坍落筒必须是按照一定的尺寸设计加工完成．

References

[1] 缪协兴,钱鸣高. 中国煤炭资源绿色开采研究现状与展望[J] .采矿与安全工程学报,2009,26(1):1-14.MIAO Xiexing, QIAN Minggao. Research on green mining of coal resources in China: current status and future prospects[J]. Journal of Mining & Safety Engineering, 2009, 26(1):1-14.

[2] 赵才智,周华强,柏建彪,等. 膏体充填材料强度影响因素分析[J]. 辽宁工程技术大学学报自然科学版, 2006,25(6) :904-906.ZHAO Caizhi, ZHOU Huaqiang, BAI Jianbiao, et al.Influence factor analysis of paste filling material strength[J]. Journal of Liaoning Technical University: Natural Science, 2006, 25(6): 904-906.

[3] 刘晓辉,吴爱祥,王洪江,等. 深井矿山充填满管输送理论及应用[J]. 北京科技大学学报, 2013, 35(9)：1113-1118.LIU Xiaohui, WU Aixiang, WANG Hongjiang, et al.Full-flow transport theory and its application in deep mine back-filling[J]. Journal of University of Science and Technology Beijing, 2013, 35(9)：1113-1118.

[4] 黄玉诚, 武洋,常军. 似膏体巷式充填采煤技术及应用[J]. 煤炭科学技术, 2014, 42(1): 37-39.HUANG Yucheng, WU Yang, CHANG Jun. Application and technology of coal mining with paste-like roadway backfill[J]. Coal Science and Technology, 2014, 42(1):37-39.

[5] 丁德强.矿山地下采空区膏体充填理论与技术研究[D].长沙:中南大学,2007.DING Deqiang. Study on the theory and technology of paste backfill in underground mining[D]. Changsha:Central South University, 2007.

[6] TATTERSALL G H, BANFILL P F G. The rheology of fresh concrete[M]. Marshfield: Pitman Publishing, 1983.

[7] MURATA J. Flow and deformation of fresh concrete,Mater[J]. Constr.1984, 17(98): 117-129.

[8] CHRISTENSEN G. Modeling of flow properties of fresh concrete:the slump test[D].Princeton:Princeton University,1991.

[9] PASHIAS N, BOGERA D V, SUMMERS J et al. A fifty cent rheometer for yield stress measurement [J]. Journal of Rheology, 1996, 40(6):1179-1189.

[10] CLAYTON S, GRICE T G, BOGER D V. Analysis of the slump test for on-site yield stress measurement of mineral suspensions[J]. International of Journal of Mineral Processing, 2003, (70):3-21.

[11] SCHOWALTER W R, CHRISTENSEN G. Toward a rationalization of the slump test for fresh concrete:Comparisons of calculations and experiments [J]. Journal of Rheology, 1998, 42(4):865-870.

[12] AARON W S, HAMLIN M J, SURENDRA P S. A generalized approach for the determination of yield stress by slump and slump flow [J]. Cement and Concrete Research, 2004(34):363-371.

[13] JEWELL R J, FOURIE A B. Paste and thickened tailings-a guide [M].Perth: Australian Centre for Geomechanics, 2006.