微积分知识在经济中的应用

□ 章腊萍

微积分在经济中有很多的应用，如一元函数微分学在边际分析中的应用，一元函数积分学在求原经济函数中的应用，求最优化问题等，这些都是众所周知的应用，除此之外，本文给出了其他微积分知识在经济中的应用，如极限、偏导数、微分方程在经济中的应用。

一、极限在经济中的应用

利息是指借款者向贷款者支付的报酬，它是根据本金的数额按一定比例计算出来的，利息又有存款利息、贷款利息、债券利息、贴现利息等几种主要形式。复利计算公式 Am=A(1+r)m，其中A表示刚开始的本金，r表示每一期的利率，m表示复利的总期数，Am表示m年后的余额。如果年利率为r的利息一年支付一次，那么当初始存款为A元时，t年后余额则为At=A(1+r)2。如果年利率为r的利息一年支付n次，那么当初始存款为A元时，t年后余额At则为At=A(1当 n→∞，这称为连续复利。

例1设某酒厂有一批新酿的好酒，如果现在(假定t=0)就售出，总收入为Ro元，如果窖藏起来，待来日按陈酒价格出售，t年末总收入为假定银行的年利率为r，并以连续复利计算，试求窖藏多少年售出可使总收入的现值最大，并求r=0．06时的t值。

解:根据连续复利公式，这批酒在窖藏t年末售出总收入为A(t)=Re-n的现值为A(t)=Re-rt，而，故 A(t)，得驻点，则有，于是是极大值点即最大值点，故窖藏年售出，总收入的现值最大，当r=0．06时年。

二、偏导数在经济中的应用

与一元经济函数的导数类似，多元经济函数的偏导数也有其经济意义，下面以需求函数为例来说明。

设某产品的需求量为Q=Q(P，y)，其中P为该产品的价格，y为消费者收入。△PQ=Q(P+ △P，y)-(P，y)，△yQ=Q(P，△y)-(P，y表示当价格为P，消费者收入为y时，Q对于P的变化率表示当价格为P，消费者收入为y时，Q对于y的变化率，称为需求Q对价格P的偏弹性，称为需求Q对收入y的偏弹性。

例2厂家生产的一种产品同时在两个市场销售，售价分别p1和p2，销售量分别为 q1和q2，需求函数分别为 q1=24-0．2p1和 q2=10-0．05p2，总成本函数为 C=35+40(q1+q2)，试问:厂家如何确定两个市场的售价，能使其获得的总利润最大?最大总利润为多少?

解:总收入函数为 R=p1q1p+p2q2=24p1-0．2p21-0．05p22，总利润函数为 L=R-C=32p1-0．2p1-0．05p22-1395+12p2，由极值的必要条件，得方程组:

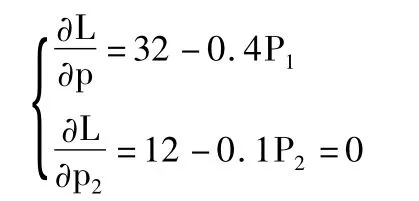
解此方程组得P1=80，P2=120。

由问题的实际含义可知，当P1=80，P2=120时，厂家所获得的总利润最大，其最大总利润为LP1-80 P1-120=605。

三、微分方程在经济中的应用

含有未知数的导数(或者微分)的方程，称为微分方程。一般写成 F(x，y，y＇，A，y(n))=0 或 y(n)=f(x，y，y＇，A，y(n-1))。微分方程的解:若将函数代入微分方程，使方程成为恒等式，则该函数称为微分方程的解，即设y=y(x)在区间I上连续且有直到 n 阶的导数，使 F(x，y(x)，y＇(x)A ，y(n)(x))=0则称y=y(x)为该微分方程在区间I上的一个解。

变量可分离方程的解:能写成y＇=f(x)g(y)形式的方程称为变量可分离型方程，其解法为:

例3已知某商品的需求量x对价格p的弹性η=-3p3而市场对该商品的最大需求量为1(万件)，求需求函数。

例4已知某商品的需求量D和供给量S都是价格p的函数:D=D(p)=，S=S(p)=bp，其中 ɑ＞0，b＞ 0 为常数;价格p是时间t的函数且满足方程:=k［D(p)-S(p)］(k为正的常数)，假设当t=0时价格为1，试求:

(1)需求量等于供给量时的均衡价格pe;(2)价格函数p(t);(3(t)。

［1］吴赣昌．微积分(经管类)［M］．北京:中国人民大学出版社，2014，第4 版

［2］李永乐，李正元．数学复习全书［M］．北京:国家行政学院出版社，2013

［3］张宇，杨超．高等数学18讲［M］．北京:北京理工大学出版社，2013