基于H∞次优滤波的速度+角速度传递对准研究*
2015-01-19程建华徐英蛟李美玲
程建华, 徐英蛟,2, 李美玲
(1.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001;2.91851部队,辽宁 葫芦岛 125000)
基于H∞次优滤波的速度+角速度传递对准研究*
程建华1, 徐英蛟1,2, 李美玲1
(1.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001;2.91851部队,辽宁 葫芦岛 125000)
针对舰船机动性能差,以及舰船高频振颤等不确定性干扰因素影响惯导系统传递对准滤波效果的问题,提出了基于H∞次优滤波的“速度+角速度”匹配传递对准方法。首先分析了影响传递对准性能的关键要素,确定了适用于弱机动特性的舰船用惯导系统传递对准方案。在此基础上,设计“速度+角速度”匹配传递对准的H∞次优滤波器,解决不确定性外部干扰的影响。给出了设计方法和滤波器解算流程。比对仿真结果表明:对于不确定性有色噪声干扰,H∞次优滤波具有很强的鲁棒性,能够完成对失准角的估计,更加符合舰船实际应用条件。
捷联式惯导系统; 传递对准; 速度+角速度匹配; H∞次优滤波
0 引 言
初始对准的精度和快速性是影响舰载武器作战性能的重要因素[1]。基于舰船主惯导和舰载武器惯导匹配的传递对准,能有效克服传统自主式对准方式在精度与时间的矛盾,以及惯性器件影响对准精度等方面的问题,成为了适用于舰载武器惯导系统初始对准的快速动基座对准方法。
匹配和滤波方法是研究和提升传递对准效果的核心技术。传递对准依据选取量测量的不同分为速度匹配、位置匹配等计算参数匹配法,以及比力匹配、角速度匹配等量测参数匹配法。采用单一参数匹配时,传递对准会受到很大限制,例如:速度匹配虽然可以快速实现水平对准,但要求舰船做S形机动,这大大增加了对舰船操纵控制的要求。因此,基于复合观测信息的传递对准方法,如“速度+姿态”、“速度+角速度”等具有对准时间短、精度高等优点,成为了舰船惯导传递对准的研究发展方向。
然而,基于匹配法的传递对准在受到环境干扰较强时,对准性能将降低,主要的原因如舰船受海浪引起的高频振颤等致使匹配方法对准滤波过程中受到有色噪声干扰,加之存在系统建模误差,从而导致滤波器性能降低,严重时可能导致滤波器发散。目前针对有色噪声干扰的处理方法通常是扩充挠曲变形为状态变量,用适应性较强的二阶Markov过程对舰体动态变形进行建模,可以适应一定的精度要求[2]。但是有些复杂海况难以用Markov过程模拟,进而导致滤波器发散。另一种比较常用的处理方法是模糊自适应滤波技术[3],通过自适应调整滤波器参数能有效克服外界噪声干扰,达到不错的滤波效果。但从设计上来说,模糊自适应滤波方案较为复杂,不利于工程实践。
H∞次优滤波算法具有较强的鲁棒性能,能保证一切具有有限能量的干扰信号最大的估计误差在一定范围内,对系统参数变化的敏感性不强[4],能够有效解决实际海况下干扰不确定等问题。
本文设计并完成了基于H∞次优滤波的“速度+角速度”传递对准方法,这对于提高不确定干扰情况下的传递对准效果,具有重要的实际意义。
1 影响传递对准性能的关键要素分析
1.1 坐标系定义

1.2 传递对准状态空间建模
选取“速度+角速度”和“速度+姿态”两种传递对准方法,选取状态变量
X=[δvxδvyφmxφmyφmzφaxφayφaz]T,
(1)
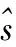
由此得到“速度+角速度”和“速度+姿态”匹配法的传递对准状态空间模型为[5]

(2)
其中
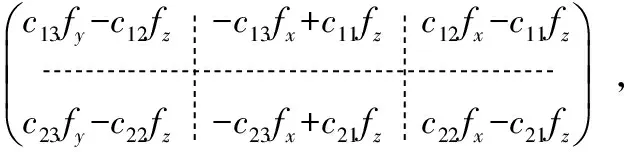
W=[wvxwvywφmxwφmywφmzwφaxwφaywφaz]T,
V=[vvxvvyvφmxvφmyvφmz]T。

对于“速度+角速度”匹配,其量测量为
Z=[Zv|Zω]T=[δvxδvy|δωxδωyδωz]T.
(3)
对应量测矩阵为

对于“速度+姿态”匹配,其量测量为
Z=[Zv|Zθ]T=[δvxδvy|δθxδθyδθz]T.
(4)
对应量测矩阵为

1.3 弱机动下传递对准性能分析
受到舰船机动特性差的影响,设计在“摇摆”状态下能快速完成对准的传递对准方法,是非常适用于舰船的传递对准方法。
选取舰船典型海况下的摇摆模型为[6]

两种不同匹配方法在相同摇摆模型下传递对准的仿真结果如图1所示。

图1 传递对准失准角估计的比对仿真结果Fig 1 Comparison simulation results of transfer alignment misalignment angle estimation
通过仿真可以看出:两种匹配方法对安装误差角的可观测度都比较高,仅通过“摇摆”均能完成失准角估计,但“速度+角速度”匹配法在快速性方面明显优于“速度+姿态”匹配法。这是因为前者应用的是线运动信息和角运动信息,后者应用的是线运动信息和角运动信息的积分,快速性有所降低。
1.4 挠曲变形对传递对准性能的影响
挠曲变形带来的不确定量测量干扰不满足传统Kalman滤波器对噪声的要求,这使得滤波器性能下降甚至发散。
舰船高频振颤引起的线速度为[7]
vDHi-ADHicos(ωDHit+φDHi)/ωDHi.
(5)
其中,ADHx=4.2gn,ADHy=3.8gn,ADHz=4.0gn;ωDHi=2πfDHi,fDHy=250 Hz,fDHz=400 Hz;φDHi为[0 2π]上服从均匀分布的随机相位。
将高频振颤等效为挠曲变形引入系统模型,可得传递对准仿真曲线如图2所示。
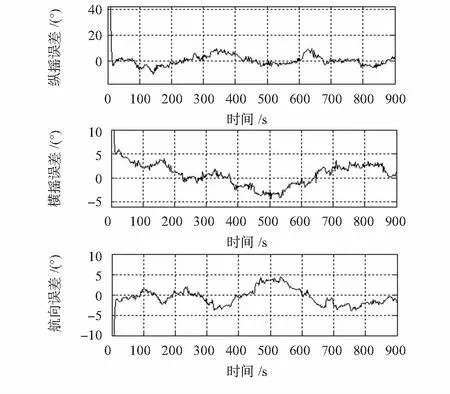
图2 有色噪声干扰下Kalman滤波器对失准角估计Fig 2 Kalman filter estimate misalignment angle under interference of colored noise
由图2可以看出:考虑挠曲变形后Kalman滤波器出现较大幅度的振荡,不具有鲁棒性,不能完成对失准角的估计。基于此,引入抗干扰性较强的鲁棒滤波技术,对于抑制不确定干扰的影响,具有较强的实际意义。
2 H∞次优滤波器设计
2.1 H∞滤波设计
舰船受随机扰动引起的挠曲变形角速度相对于舰船运动角速度是个小量,通常将其视为动态量测误差。
设线性离散系统的系统方程与量测方程为
(6)
式中Xk+1为被估计状态,Zk为系统的量测量,Φk为一步转移矩阵,Γk为系统噪声矩阵,Hk为系统量测矩阵,Wk和Vk分别为系统的状态噪声和量测噪声。
一般情况下,需要利用量测量对系统状态向量的线性组合Sk=LkXk进行估计。其中,Lk为给定的状态向量线性变换矩阵。由于估计状态量为Xk,因此,Lk=I。
(7)
用TK(F)表示初始状态误差(X0-0)、未知干扰信号序列和到滤波误差k的传递函数矩阵。
使得|TK(F)||达到最小的值即为H∞最优滤波器的最优解[8]
(8)
式中 ∏0为反映X0的初始假设0与真实值X0接近程度的正定矩阵。
由于H∞最优滤波的解只有对某些特殊问题才可获得,工程实践中通常求取次优解。次优解只需要满足参数γ>γ0即可。
2.2 H∞次优滤波递推解算
针对式(6)所示系统,对于给定常数γ>0,如果矩阵[ΦkΓk]行满秩,则H∞次优滤波问题有解的充要条件为[9~10]
(9)
式中Pj为Riccati方程的解。
从式(9)可以看出,H∞滤波器次优解的确定,主要取决于参数γ。为了确定参数γ,首先给出如下定理。
定理1[11]:设A和B为两个n阶Hermite阵,A>0,B≥0,则A>B,当且仅当λmax(BA-1)<1,λmax(·)表示矩阵的最大特征值。
由定理1和式(9)可得
γ=σ{λmax[LT(k)L(k)(P-1(k)+HT(k)H(k))-1]}1/2,
(10)
式中λmax[·]表示最大特征值,系数σ>1,根据工程实际应用情况确定σ的大小。
由此可得H∞次优滤波器具体滤波过程为:
(11)
2)H∞滤波增益矩阵Kk
(12)
(13)
4)估计误差协方差Pk+1|k
(14)

通过观察H∞次优滤波器的滤波过程可以看出,当参数γ趋近于无穷大时,其增益Kk变为Kalman滤波器的增益,此时H∞次优滤波器等价于Kalman滤波器。因此,可以说Kalman滤波器是H∞次优滤波器的一种特殊形式。
在满足式(9)的条件下,不断减小γ的值,直到γ达到最小,此时H∞次优滤波器的解逼近H∞最优滤波解,滤波器的鲁棒性最好,但式(14)的估计误差协方差不一定最小;当γ趋近于无穷时,滤波器具有最小的估计误差协方差,但此时的鲁棒性最差。通过选取适当的γ值,可以使滤波器既达到较小的协方差有具有较好的鲁棒性。
3 系统仿真与结果分析
设定φ=45.779 6°,λ=126.670 5°,φa=[0.1° 0.1°0.1°],gn=9.780 49 m/s2,ωie=7.272 204 17 rad/s,采样周期Tn=0.1 s,γ=30。
滤波器初始值设定为
P0=diag{(0.1 m/s)2;(0.1 m/s)2;(0.1°)2;(0.1°)2;(0.1°)2;(0.1°)2;(0.1°)2;(0.1°)2}.
对干扰噪声为白噪声和有色噪声时的失准角进行估计,仿真曲线分别如图3、图4所示。

图3 白噪声干扰下的失准角估计Fig 3 Misalignment angle estimation under interference of white noise

图4 有色噪声干扰下的失准角估计Fig 4 Misalignment angle estimation under interference of colored noise
通过仿真可以看出:无需舰船做大幅度机动,只需在系泊条件跟随海浪摇摆情形下,“速度+角速度”匹配法传递对准就可完成快速传递对准。而且,由仿真曲线可知,干扰噪声为白噪声时,Kalman滤波器和H∞次优滤波器都能很好地对失准进行估计,由于Kalman滤波器的估计误差协方差较H∞次优滤波器的小,因而性能更好;当干扰噪声为有色噪声时,Kalman性能下降,收敛速度明显低于H∞次优滤波器,而H∞次优滤波器能很好地估计出失准角,具有很强的鲁棒性。
4 结 论
“速度+角速度”匹配传递对准能够在舰船无需大幅度机动条件下快速完成初始对准,且具有较高的精度。针对外界干扰的未知性,传统Kalman滤波器难以实现对失准角的估计,而H∞次优滤波器,既能快速完成初始对准,又保证了系统的鲁棒性。因此,本文设计的基于H∞次优滤波器“速度+角速度”匹配传递对准方法能够满足实际航行条件下的动基座初始对准方法。更加符合工程应用的实际情况,是一种行之有效的估计方法。
[1] 程建华,陈岱岱.舰船姿态辅助DGPS的传递对准精度评估方法[J].哈尔滨工程大学学报,2012,33(12):1509-1514.
[2] 高青伟,赵国荣,王希彬,等.传递对准中载舰挠曲变形和杆臂效应一体化建模与仿真[J].航空学报,2009,30(11):2172-2177.
[3] 秦永元,朱新颖,赵长山,等.舰载机捷联惯导自对准方案与仿真[J].中国惯性技术学报,2008,16(1):28-33.
[4] 岳晓奎,袁建平.H∞滤波算法及其在GPS/SINS组合导航系统中的应用[J].航空学报,2001,22(4):366-368.
[5] 于 飞.速度加角速度匹配传递对准方法研究[J].传感器与微系统,2009,28(6):69-72.
[6] 孙昌跃,邓正隆.大方位失准角的舰载武器INS对准[J].中国惯性技术学报,2008,16(5):534-542.
[7] 王勇军,徐景硕,袁 涛.基于H∞滤波的舰载机惯导海上自对准方法[J].中国惯性技术学报,2012,20(5):536-539.
[8]HassibiB,SayedAH,KailathT.LinearestimationinKreinspaees—partII:Application[J].IEEETransactionsonAutomatieControl,1996,41(1):34-49.
[9] 宋金来,弥 曼,张 军,等.基于H∞滤波技术的传递对准方法[J].中国惯性技术学报,2007,15(6):646-649.
[10]CollinsEG,SongT.RobustH∞estimationandfaultdetectionofuncertaindynamicsystems[J].JournalofGuidance,ControlandDynamics,2000,23(5):857-864.
[11] 王松桂,吴密霞,贾忠贞.矩阵不等式[M].2版.北京:科学出版社,2006:48-56.
徐英蛟,通讯作者,E—mail:361224791@qq.com。
Research on velocity and angular velocity matching transfer alignment based on H∞ suboptimal filtering*
CHENG Jian-hua1, XU Ying-jiao1,2, LI Mei-ling1
(1.College of Automation, Harbin Engineering University,Harbin 150001,China;2.Unit 91851 of PLA,Huludao 125000,China)
Aiming at problem of poor maneuvering performance of ship,and uncertain disturbance factors such as high-frequency vibration of ships influences inertial navigation system transfer alignment effect,a new method of velocity and angular velocity matching transfer alignment based on H∞ suboptimal filter is proposed.By analyzing the critical factors influencing performances of transfer alignment,determines the method of inertial navigation system transfer alignment suitable for weak mobility characteristics of ships.On this basis,design H∞ suboptimal filter for velocity and angular velocity matching transfer alignment to solve influence of external disturbance.Design method and filter resolving process.Comparison simulation results show that H∞ suboptimal filtering is obviously better when interference noise is colored ,it has a strong robustness,and more according with actual sailing ships.
SINS; transfer alignment; velocity and angular velocity matching; H∞ suboptimal filtering
10.13873/J.1000—9787(2015)12—0043—04
2015—03—13
国家自然科学基金资助项目(61374007,61273081); 中央高校基本科研业务费专项资金资助项目(HEUCFX41309)
U 666.1
: A
: 1000—9787(2015)12—0043—04
程建华(1977-),男,山东莱阳人,博士,副教授,主要研究方向为惯性导航与定位技术、组合导航技术。
