基于优化的果蝇算法的光伏MPPT仿真研究
2015-01-18王素宁潘三博杨青斌林成栋
王素宁,潘三博,杨青斌,林成栋
(1.上海电机学院电气学院,上海201306; 2.中国电力科学研究院新能源研究所,江苏南京210003)
基于优化的果蝇算法的光伏MPPT仿真研究
王素宁1,潘三博1,杨青斌2,林成栋1
(1.上海电机学院电气学院,上海201306; 2.中国电力科学研究院新能源研究所,江苏南京210003)
光伏阵列在不同的光照强度和温度等外界环境下,其I-V和P-V输出特性曲线呈非线性。为了提高光伏发电系统的发电效率,对其进行快速和精准的最大功率跟踪显得尤为重要。果蝇算法是一种求解函数极值的新算法,其具有收敛速度快且准确的特点,因此,在建立光伏阵列的数学模型基础上,提出了一种改进的果蝇算法的光伏最大功率跟踪方法,并通过在Matlab中仿真,与粒子群跟踪算法的跟踪性能进行了对比,证明了该算法在光伏最大功率跟踪方面的快速性和有效性。
光伏阵列;最大功率跟踪;Matlab仿真;改进的果蝇算法
0 引言
随着光伏发电系统在世界范围内的广泛应用,光伏发电系统也渐渐暴露出了许多问题。其中最突出的问题就是光伏发电系统效率偏低,光伏电池不能完全地发挥其效能。要解决此问题,提高光伏发电系统的跟踪效率是其必经之路,即,寻找更优良的光伏最大功率跟踪控制算法是必要的[1-2]。通过提高光伏发电系统的跟踪效率,进而改善整个系统的发电效率。
2011年7 月,台湾大学教师潘文超博士提出一种新的智能优化算法——果蝇算法。果蝇算法源于提出者对果蝇觅食行为观察后,总结模拟果蝇在寻找食物的过程中的行为,这种算法可广泛应用于科学和工程领域[3-4]。
目前已经存在的最大功率跟踪方法有固定电压法(constant voltage tracking,CVT)、扰动观察法(perturbation&observation,P&O,俗称爬山法)、电导增量法(incremental conductance,INC)和粒子群算法(particle swarm optimization,PSO)[5]等。但它们都有自身的不足,如动态特性不好,不能应对外界环境的变化,当环境温度、光照强度的变化等,跟踪到最大功率点后会在其附近来回振荡,损失掉部分能量。针对上述情况,利用果蝇算法在求解目标函数最大值收敛速度极快的特性,提出一种改进的果蝇优化算法实现最大功率跟踪的方法,能够克服以上问题,实现快速、精确、振荡较小地得到光伏电池最大功率点,减少功率损耗。
1 光伏阵列数学模型和输出特性研究
1.1 光伏电池工程模型
光伏电池的等效模型[6-7],根据电子学理论,光伏电池的等效电路如图1所示。
根据图1,忽略结电容Cj,可以得到光伏电池的I-U特性曲线方程为[8]


图1 光伏电池等效电路
式中:IL为光电流,A;I0为反向饱和电流,A;q为电子电荷(1.6×1 019 C);K为玻耳兹曼常数(1.38× 10-23 J/K);T为绝对温度,K;A为二极管因子;RS为串联电阻,Ω;Rsh为并联电阻,Ω。对电路模型简化处理,推导得出一个方便计算最大功率的工程模型,即式(2)。
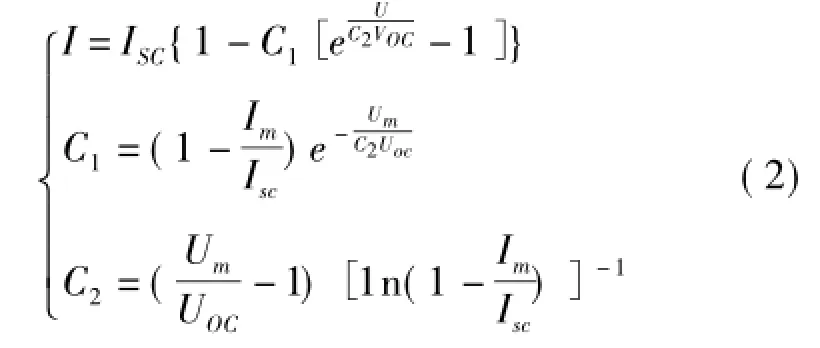
光伏阵列是由若干太阳能电池板根据负载容量大小要求,通过串并联的方式组成较大功率的装置。因此,光伏阵列和单个电池板之间有如下关系:

式中:V为光伏电池板的输出电压;I为光伏电池板的输出电流;P为光伏电池板的输出功率;Ns为太阳能电池板串联数目;Np为太阳能电池板并联数目;VN为光伏阵列的输出电压;IN为光伏阵列的输出电流;PN为光伏阵列的输出功率。
1.2 光伏阵列输出特性曲线
采用尚德公司的光伏电池板,在标准测试下参数为:Vmp=36.4 V,Imp=5.34 A,VOC=45.3 V,ISC= 5.67 A,Pmax=196 W。光伏阵列在受到外界不同的光照条件下,其I-V和P-V输出特性曲线如图2、图3所示。
由图2和图3看出温度相同时,随着光照强度的增加开路电压几乎不变,短路电流增加变化较大,最大功率也有所增加。
通过图2、图3仿真结果可以得出以下结论:太阳能电池由于光照强度等环境因素影响很大,其输出具有明显的非线性。基于光伏电池输出特性具有非线性和最大功率点的特点;而且最大功率点也随着光照强度和环境温度等因素变化,为提高能量转换效率,在实际应用中光伏电池需采用适当的最大功率点跟踪算法控制光伏系统,保证光伏电池总是运行在最大功率点。

图2 不同光照强度下的I-V特性曲线

图3 不同光照强度下的P-V特性曲线
2 果蝇优化算法原理
2.1 果蝇算法在最大功率跟踪上应用分析
果蝇算法是一种模仿果蝇觅食行为的寻优新方法,果蝇寻找食物先依靠灵敏的嗅觉判断与食物的大致距离,再利用视觉向食物方向靠近,多个果蝇一起觅食就构成一种群体智能寻优算法[9-10]。
目前果蝇算法已经成功应用到数据挖掘技术、Z-SCORE模型系数、广义回归神经网络参数优化、支持向量机参数优、最大功率分类预测和求解数学函数极值等领域[11-12]。
光伏最大功率跟踪的过程实质就是对光伏阵列建立的目标函数进行最优值寻找的过程,即找到公式(5)的最大值。果蝇算法在寻找目标函数最优值方面具有较好的收敛性,每个果蝇个体根据自己的嗅觉先判断出光伏最大功率点的具体位置,然后通过沿着横坐标和纵坐标按照一定的步长飞行逐步靠近最大值,通过比较每个果蝇个体的最优值,得到果蝇种群的最优值。果蝇群体迭代搜索食物示意图4所示。

图4 果蝇群体迭代搜索食物示意图
2.2 果蝇算法的步骤
1)首先对果蝇群体位置的初始化,初始化结果为initU_axis;initP_axis(U代表电压值,P代表功率值);
2)设定电压和功率搜索方向为随机函数rand()产生一个[0,1]的步长,则电压和功率的随机搜索坐标便可以通过下面的公式获得。
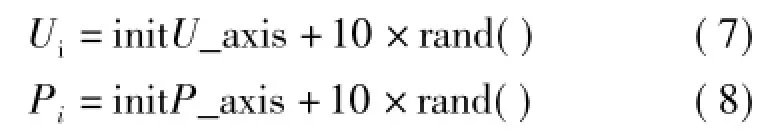
3)由于最大值位置不可知,因此需要估计光伏电压和功率当前位置和原点之间的距离Disti,之后计算最大值判定值Si,Si等于距离Disti的倒数。

4)将各个味道浓度判定值代入味道浓度判定函数Fitness(适应值函数),并找出群体最优果蝇位置和最优值,将Si代入最大值判定函数Function中,将公式(5)带入味道浓度判定函数,寻找出光伏阵列当前位置的最大值。
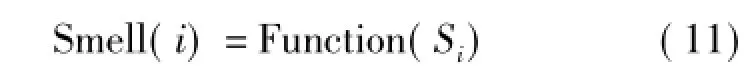
5)光伏阵列最大值由式(12)获得。

6)保留光伏阵列当前最大值和与其对应的电压和功率坐标,这时果蝇群体通过自身的视觉对食物源进行定位,之后飞向最大值所在的位置。

7)进入迭代寻优,重复迭代步骤2)~5),同时判断最大值是否大于前一迭代局部最大值;若成立,则执行步骤6)。
从以上步骤可发现果蝇优化算法只需设定种群规模群、搜索半径和种群繁衍代数,其参数设定方便,算法结构简单,易于编程实现。
2.3 改进的果蝇优化算法
由步骤2)中的公式(7)和公式(8)可以明显看出,横纵坐标的初始位置是一个随机分布函数,搜索范围很大,经过公式(9)和公式(10)将味道浓度判定值Si变得很小;这时将味道浓度作为判定函数,找到最优值很慢,因此在横纵坐标迭代区间进行缩小,将电压和功率值分别归一化为无量纲的数值,将其范围归一化到(0,1)区间,即将上述的步骤3)中由Ui和Pi计算得到Si的自变量进行归一化,即

式中:VOC为光伏开路电压;Pmp为光伏给出的额定功率。
将式(16)、式(17)的电压和功率新坐标重新带入式(9)、式(10)得到新的Di1和Si1再带入步骤4)式(11)中的判定函数Function中重新计算。
当迭代结束,找到最大功率值时进行反归一化,将电压和功率坐标值反归一化为真实值。将步骤6)式(14)、式(15)中的电压和功率坐标进行改写为
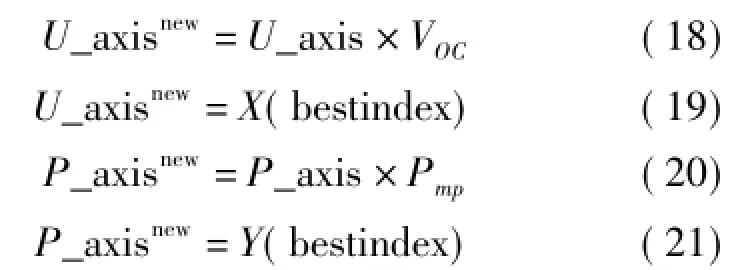
依照这个思路,使得果蝇算法得到优化。在精度不减小的条件下,为了进一步加快搜索范围,优化的果蝇算法采用变步长进行搜索迭代。在迭代过程中采用新的坐标

图5 软件流程图

将得出的果蝇每个个体最优值进行比较,得出最大值,设定一个误差值Eerror,当最大值与理论值差值的绝对值小于Eerror时,即│Smellbest-Pmax│<Eerror并且到达最大迭代次数,则停止迭代。
具体详细流程图参考图5。
3 实验结果分析
在光伏电池温度T=25℃、辐射强度R=1 000 W/m2的情况下对果蝇优化方法和PSO进行仿真实验。仿真结果如图6所示。
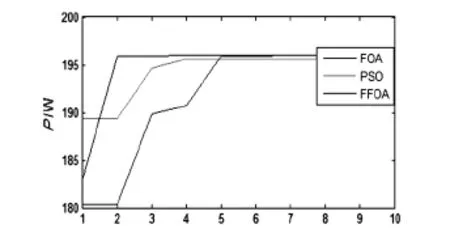
图6 3种算法仿真结果对比
4 对比与结论
通过仿真验证,从图6中得出改进的果蝇优化算法在跟踪速度方面比PSO具有明显优势。该算法原理简单,实现起来方便,在寻找光伏阵列最大值上收敛速度特别快。具体表现在以下4个方面:
1)种群规模:果蝇优化算法的种群规模为20,PSO的种群规模30,改进的果蝇优化算法种群规模仅为10。
2)计算量:在同样的迭代次数下,改进的果蝇优化算法跟踪到最大功率点的种群规模少,需要设定的参数少,PSO需要设置PopSize(种群规模)、MaxIt(迭代次数)、iter=0(标志位)、maxw(最大惯性权值)、minw(最小惯性权值)、w(每一步惯性权值)、interdec(每一步惯性权值变化量)、popul(位置参数)、vel(速度参数)、c1(速度方向迭代计算系数)、c2(速度方向迭代计算系数)等参数。而改进的果蝇优化算法只需要PopSize(种群规模)、MaxIt (迭代次数)、InitX_axis和InitY_axis(初始位置和方向参数);两者相比较,改进的果蝇优化算法在参数设置方面节省程序空间,程序运行需要的时间快。
3)快速性:果蝇优化算法和PSO算法需要迭代5次才能跟踪上,而改进的果蝇优化算法第2次就能跟踪上。
4)精确度:光伏最大功率值的理论值是196 W,果蝇优化算法得到的数值为195.987 W,比PSO的精确度要高。
具体对比结果如表1所示。

表1 算法运行结果对比
该算法还存在一定的缺点:由于光伏最大值判定取值为距离的倒数,它限定了变量的取值为正,同时限制了它的使用范围;并且收敛容易陷入局部最大值,稳定性也有待进一步研究。
改进:针对陷入局部极值问题可以采用和其他智能算法或者数学方法结合,扩大收敛范围。
[1]高志强,王建赜,纪延超,等.一种快速的光伏最大功率点跟踪方法[J].电力系统保护与控制,2012,40 (8):105-109.
[2]赖东升,杨苹.一种应用于光伏发电MPPT的变步长电导增量法[J].电力电子技术,2012,46(3):40-42.
[3]潘文超.果蝇最佳演化算法一最新演化式计算技术[M].台湾:沧海书局,2011.
[4]潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报,2011,29(4):1-5.
[5]陈剑,赵争鸣,袁立强.等.光伏系统最大功率点跟踪技术的比较[J].清华大学学报(自然科学版),2010,50(5):700-704.
[6]苏建徽,余世杰,赵为,等.硅太阳电池工程用数学模型[J].太阳能学报,2001,22(4):409-412.
[7]茆美琴,余世杰,苏建徽.带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报,2005,17 (5):1248-1251.
[8]万晓凤,张燕飞,余运俊,等.光伏电池工程数学模型的比较研究[J].计算机仿真,2014,31(3):113-117.
[9]韩俊英,刘成忠.自适应混沌果蝇优化算法[J].计算机应用,2013,33(5):1313-1316.
[10]张勇,夏树发,唐东生,等.果蝇优化算法对多峰函数求解性能的仿真研究[J].暨南大学学报,2014,35 (1):82-87.
[11]雷秀娟,史忠科,周亦鹏.PSO优化算法演变及其融合策略[J].计算机工程与应用,2007,43(7):90-93.
[12]靳其兵,赵振兴,苏晓静,等.基于粒子健康度的快速收敛粒子群优化算法[J].化工学报,2011,62(8):
2328-2333 .
王素宁(1990),硕士研究生,主要研究方向为光伏发电技术;
潘三博(1974),副教授,硕士生导师,主要研究可再生能源光伏发电及储能技术、高效率电力电子变换器、谐振逆变器等方面;
杨青斌(1988),助理工程师,主要研究方向为新能源发电及其并网检测;
林成栋(1991),硕士研究生,主要研究方向为光伏逆变器设计。
Under different sun light and temperature of the external environment,the I-V and P-V output characteristic curves of photovoltaic(PV)array are nonlinear.In order to improve the efficiency of photovoltaic power generation system,it is important to track the maximum power point quickly and accurately.Fruit fly algorithm is a kind of new algorithm to solve the extremum of function,it has a quick and accurate convergence speed,therefore,a kind of improved fruit fly algorithm for photovoltaic maximum power point tracking is proposed based on the established mathematical model of PV array.Through the simulation with Matlab,the quickness and accuracy of the proposed algorithm are verified by comparing tracking performance with particle swarm optimization algorithm.
PV array;MPPT;Matlab simulation;improved fruit fly optimization algorithm
TM615
A
1003-6954(2015)06-0001-04
2015-08-26)
上海市教委科研创新基金(14YZ160);上海电机学院科研项目(12C107)
