基于ANSYS的隧道内输气管道应力分析

任 帅，马贵阳，王海燕

（辽宁石油化工大学， 辽宁 抚顺 113001）

基于ANSYS的隧道内输气管道应力分析

任 帅，马贵阳，王海燕

（辽宁石油化工大学， 辽宁 抚顺 113001）

隧道内的弯管处通常是应力集中的地方，使得管道处于危险甚至失效状态。为了研究隧道内弯管在不同情况下的受力，利用有限元分析软件ANSYS建立弯管的有限元模型，明确了隧道内垂直L型和Z型弯管的应力分布情况和应力集中点。研究结果表明：在试压和运行状态下，弯头处所受的应力最大，管道内压是引起管道应力的主要因素。隧道内管道最大应力随管道半径的增大而逐渐增大，呈近似线性关系。不同形状的弯管结构分布会对弯管的应力分布产生影响。L型弯管的最大应力随两臂长的增加先增大后减小，Z型弯管的最大应力随相互平行的两弯管的增大而逐渐增大。

隧道；输气管道；试压工况；有限元分析；半径；臂长

随着我国输气管道建设高峰时期的到来，在山区敷设管道时，为了减少植被破坏、防止水土流失等自然灾害的发生，隧道穿越形式被广泛采纳[1]。隧道内的油气管道的设计目前没有相对可靠的理论依据，大部分设计必须依靠经验参数，此外，管道在隧道内的应力分布情况模糊，使得管道的运行存在很大的隐患[2]。导致管道失效的因素有管道腐蚀，管道疲劳，设计不合理等，除此之外还有一个经常被忽略的重要原因，就是在隧道内存在一些特殊管段，诸如弯头等常常会产生应力集中，这使得管道不能满足强度要求而失效[3-6]。国外的管道在“L”和“Z”段可能产生横向位移处增加软泡材料，如废聚氨脂，泡沫塑料。而目前我国并没有采取相应措施，在小管径和温差较低时弯头部位应力未达到材料的强度极限，仍可正常运行，但当运行管道管径，温差较大时会造成管道破裂[7,8]。

管道施工中一个非常重要的程序是管道试压，不仅是对管道工程在生产中能否在设计压力下安全运行的一次检验，也是对管道施工质量，材料性能，管道整体性能的一次综合检验[9,10]。《原油和天然气输送管道穿跨越设计规范》6.2.1中规定，大中型水域，铁路及Ⅱ级以上的公路穿越管段，必须独立进行强度试压和严密性试验，合格后再与相邻管段连接。本文利用有限元软件ANASYS对隧道内弯管建立有限元模型，分析由于半径,结构参数的不同而使弯管受到不同的应力应变，找出危险点，为设计施工提供一定理论指导。

1 管道的应力分类及校核[11,12]

因为管道上有载荷作用，就会产生各种各样的应力。由于外部和内部作用的影响，诸如压力、重力、温度都可能引起管道相对应应力，这些应力又可分为一次应力，二次应力和峰值应力。

由管道的内压、自重和其他外载产生的应力称为一次应力。于浦义等编写的石油化工压力管道设计手册中规定：内压、自重和外载产生的环向应力、轴向应力和剪应力等应满足外部力和力矩的平衡条件。如果应力过大，管道产生的变形将无限制的增大（即没有自限性），最终导致破坏。一次应力的大小是衡量管道能否安全运行的标准之一，为了确保一次应力不变，安装条件、内压、温度和外载必须保持不变。一次应力值小干或等于操作温度下材料的许用应力， 则管道可以安全运行。

由于管道变形受阻而引起的正应力和剪应力称为二次应力，其不是直接与外力相平衡，而是通过管道各部分变形来适应的。同时，二次应力作用的范围限制在局部范围内。热胀推力的作用可以引起管道局部屈服，从而产生少量塑性变形，此时，椎力就不会再增加，塑性变形也不再发展，这种现象称为有自限性。

根据ASME．B31.8《气体运输和分配系统的管道标准》，因为隧道内的管道处于比较封闭的环境，并建有固定墩，支墩等辅助设施，所以静力分析主要校核自重W，内压P，温度T。管道总应力叠加计算式（1）：

式中L1为计算管道系统对边界的推力。

一次应力叠加计算式：L2=W+P

式中L2为管道系统中各点的一次应力值。

二次应力叠加计算式：L3= L1-L2

式中L3为管道系统中各点的二次应力值。

输气管道穿越工程在正常投产运行前需要进行单独试压，根据SY/T0015.1-1998《原油和天然气输送管道穿越工程设计规范—穿跨工程》中规定，油气输送管道的穿越管段试压压力，试压时间和试压介质分别按国家标准GB50251和GB50253规定执行，强度验算压力按下（2）式计算，

式中

:Pt—试压压力，MPa；

δ—管道设计壁厚，mm；

σs—管道规定的屈服极限，MPa；

D—管道外径，mm。

2 管道模型的建立及应力分析

2.1 模型的建立

隧道内管道走向的平面分布如图1所示。隧道内弯管可以分为垂直型L型和Z型。管道直径813 MPa，壁厚22 mm，运行压力为6.4 MPa，根据式1，试压压力24 MPa，试压介质为水。管内温度为50 ℃，管外平均温度为10 ℃在ANSYS中选用pipe16，pipe18单元建立弯管有限元模型。定义第一类第二类材料的弹性模量为206 GPa，密度为7 850 kg/m3,泊松比为0.3。用命令“RUN”定义管道分别沿Y轴的延伸量为4.6、0.4 m，沿X轴的延伸量为0.4、4.6 m。用命令“BEND”定义弯管处半径为0.3 m，建立垂直L型弯管。用命令“RUN”定义管道分别沿X轴的延伸量为4.6、0.4 m，沿Y轴的延伸量为0.4、3.2、0.4 m，沿X轴的延伸量为0.4，4.6 m。用命令“BEND”定义两个弯管处半径为0.3 m，建立垂直Z型管道。通过以上步骤生成的管道弯管模型如图2所示。

图1 隧道穿越管道走向平面分布图Fig.1 The Distribution map of thepipeline thruogh tunnel

图2 弯管有限元模型Fig.2 The finite element model of bending pipeline

2.2 加载求解

定义Y方向的重力加速度为9.8 m/s2，定义两端点所有节点自由度。加载完成后进入求解器求解。通过通用后处理器显示应力分布情况。垂直L型Z型弯管在试压工况下的应力分布如图3所示。

图3 弯管在试压工况下的应力分布Fig.3 The stress distribution of bending pipeline under pressure testing condition

3 数值模拟结果分析

3.1 运行工况不同对最大应力的影响

通过上述分析，两类弯管在不同运行工况下X方向的最大应力值如下表1所示。从表1可知，试压工况下“L”，“Z”型管道在弯管处的应力最大，“Z”型弯管处的最大应力大于“L”型的，且最大应力发生在“Z”型管靠下边的弯管处。隧道内弯管在设计安装时必须考虑试压工况，使得管道能够满足试压时的强度要求。

表1 不同运行工况弯管应力分布情况表Table 1 The stress distribution of bending pipeline under different conditions

3.2 管道半径对最大应力的影响

由于在试压工况下管道需承受的应力最大，所以下面只考虑在试压工况下半径对最大应力的影响。图4为管道半径变化对最大应力的影响，由图可知，最大应力随半径呈近似线性关系。当隧道内管道为大半径时需考虑在弯管处增加保护措施以防管道破裂。

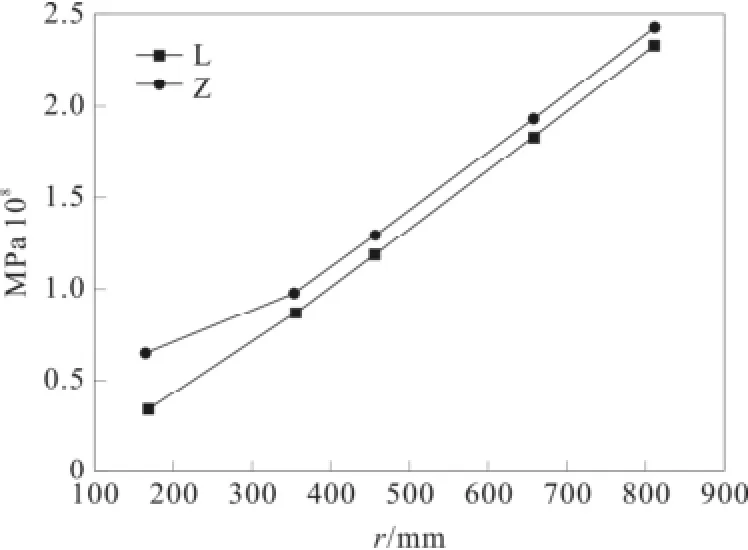
图4 管道半径变化对最大应力的影响Fig.4 The effect of pipe radius on the maximum stress

3.3 管道结构尺寸对最大应力的影响

改变“L”，“Z”型弯管的臂长，但保持两臂相等，“Z”型垂直臂保持4 m不变，相互平行的两臂变换。臂长变化随最大应力值的关系如下表2，由表可知，“L”型弯管，随着臂长变长先增大后减小。“Z”型弯管随臂长增加最大应力也增加。当“Z”型弯管两平行臂长保持10 m不变，垂直臂长由4米逐渐增加到10 m，最大应力逐渐减小，见图5。

表2 水平臂长变换对最大应力的影响Table 2 The parallel arm length influence on the maximum stress distribution of bending pipeline

图5 垂直臂长对“Z”型弯管的应力的影响情况Fig.5 Influence of vertical arm length on the stress distribution of “Z” bending pipeline

4 结 论

（1）在试压工况下，垂直L型与Z型弯管所受应力最大且最大应力产生的位置都在弯管处，加之弯管处一般有焊缝，所以弯头处为危险面。

（2）随着隧道内管道半径增加，弯管处的最大应力值增加。

（3）对于“L”型弯管，最大应力随两臂长的增大先增大后减小。对于“Z”型弯管，最大应力随相互平行臂长的增加而增大。在实际设计安装时，根据隧道实际深度、走向结合以上结论，调整特殊管段处的结构尺寸，必要时在弯头处添加软泡材料，使隧道内管道可以安全运行。

［1］ 陆悦.川气东送管道工程山岭隧道内管道安装设计[J].科技与企业，2011(4):60-61.

［2］ 岳进才.压力管道技术[M].北京：中国石化出版社，2006：13-16.

［3］ 吴晓楠，鲜燕，刘源海，等.清管过程中隧道内输气管道应力分析[J]天然气与石油，2012,30（2）:1-3.

［4］向勇.西气东输中卫黄河隧道设计[J].石油工程建设，2011，37(3):51-57.

［5］彭星煜,梁光川,张鹏,等.人工爆破地震作用下输气管道动力响应分析[J].天然气工业，2012,32（11）：81-84.

［6］唐永进. 压力管道应力分析[M]. 2版.北京：中国石化出版社，2009：51-66.

［7］郭瑞平，李广信，陈轮.“L”型直埋供热管道受力规律数值模拟[J].计算结构力学及其应运，1996,13（3）：327-332.

［8］郭瑞平，李广信.“Z”型直埋供热管道受力特性的研究[J].煤炭学报，1995,20（6）:658-663.

［9］吴晓南，舒浩纹，昝林峰，等.试压工况下盾构隧道内输气管道应力分析[J] 天然气工业，2013,33（3）:73-77.

［10］余运复，张继霞，吴俊松，等.国内外输油气站工艺管道试压标准差异分析[J].全面腐蚀控制，2014(6)：74-78.

［11］于浦义,张德姜,唐永进,等.石油化工压力管道设计手册[M].北京:化学工业出版社,2010.

［12］ 隋之锋. 输气管道特殊管段应力分析及安全性研究[D]. 中国石油大学(华东), 2009. DOI:10.7666/d.y1543071.

Stress Analysis of Gas Pipeline in Tunnel Based on ANSYS

REN Shuai，MA Gui-yang，WANG Hai-yan
（Liaoning Shihua University, Liaoning Fushun 113001，China）

The elbows in the tunnel are usually the stress concentration point. They make the pipeline be in dangerous or even failure states. In order to study the stress condition in tunnel under different conditions, the finite element analysis software ANSYS was used to build the finite element model to carry out the numerical simulation in order to find out the stress distribution and the stress concentration points in type “L” and type “Z” pipelines. The results show that, under pressure testing and operating condition, the pressure of the elbow is the highest. The inner pressure in the pipeline is the main factor to cause the stress. The maximum stress of pipeline in the tunnel gradually increases along with the pipe radius increasing, and there is an approximate linear relationship between them. The different structure of elbow can affect the stress distribution, the maximum stress on “L” pipe first increases and then decreases with the increase of arm length, but it always increases on “Z” pipe.

Tunnel; Gas pipeline; Pressure testing condition; Finite element analysis；Radius; Arm length

TE 832

： A

： 1671-0460（2015）11-2652-03

2015-04-28

任帅（1989-），男，内蒙古自治区鄂尔多斯市人，在读硕士，现就读于辽宁石油化工大学，研究方向：管道泄漏分析。E-mail：943178963@qq.com。