基于蚁群算法车辆导航系统路由选择问题的研究

车高峰 陆月然 谭 军

（百色学院信息工程学院，广西 百色 533000）

基于蚁群算法车辆导航系统路由选择问题的研究

车高峰 陆月然★谭 军

（百色学院信息工程学院，广西 百色 533000）

利用蚁群运动的遍历性、随机性和规律性特点，分析了车辆导航系统路由选择问题的蚁群优化算法，仿真结果表明该方法是一种简单有效的算法。

蚁群优化算法；车辆导航系统；路由选择问题

1 引言

在智能交通系统中车辆导航系统占据重要地位，通过地图查询、路线规划、自动导航来确定车辆最优行驶路线，为出行旅游者提供最优路线。车辆导航技术是多学科交叉的结晶，结合了导航卫星以及目标定位技术等。为了解决动态路由问题，学者提出了很多算法，如Dijkstra算法、A*算法等。上世纪90年代蚁群优化（Ant Colony Optimization）算法由意大利学者M.Dorigo等人最早提出。由于蚁群算法有较强的自适应性、鲁棒性，在寻优路径中取得了一系列较好的实验结果。本文基于蚁群算法对路由选择进行研究，同时避免在路由选择过程中陷入局部极值。

2 路由选择问题的蚁群优化算法

路由选择问题是运筹学、组合优化等领域中一个著名的难题，由于其NP难题性质，迄今尚未能彻底解决。目前求解这类问题的主要方法有模拟退火算法[1-2]、遗传算法[3]、启发式搜索法、Hopfield神经网络算法[4]等。下面简单介绍蚁群基本算法。

设某交通网络中有m辆车，每辆车有以下特征：车辆根据以地点距离和路段上外激素的数量为变量的概率函数选择下一个地点（设τ(t)为t时刻路段e(i，j)上外激素的强度）。规定车辆不允许转到刚刚到过的地点，有禁忌表控制（设tabus表示第s辆车的禁忌表，tabus(k)表示禁忌表中第k个元素）。它完成周游后，车辆在它每一条访问的路段留下外激素。

2.1 导航系统选择下一路段规则

初始时刻，各条路段上的信息激素相等，设τij(0)=C（C为常数）。车辆s(s=1,2,…,m)在运动过程中，根据各条路段上信息量决定转移方向，表示在车辆s由点i转移到地点j的概率。

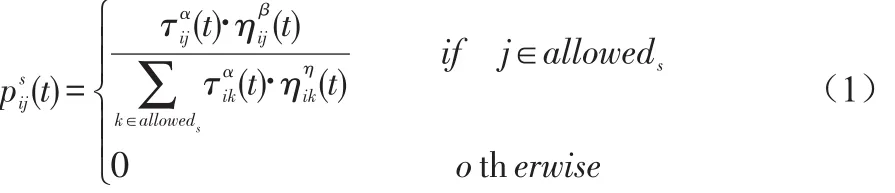
其中alloweds={0，1…，n-1}-tabus表示车辆s下一步允许选择的交通地点，tabus(s=1，2，…，m)用于记录车辆s当前所走过的地点，集合tabus随着进化过程做动态调整。ηij表示路段(i，j)的能见度，利用启发式算法算出，一般取dij表示地点i与地点j之间的距离。α表示轨迹的相对重要性，β表示能见度的相对重要性。

2.2 信息更新规则

设ρ表示信息的持久性。1-ρ理解为信息衰减度。随着时间的推移，以前留下的信息逐渐消失，用参数1-ρ表示轨迹信息消逝度，经过n个时刻，车辆完成一次循环，各路径上信息量要根据以下公式调整：

2.3 车辆导航系统路由蚁群算法的基本步骤

（1）初始化迭代步数nc←0以及τij和∆τij的值,将m辆车随机置于n个地点上；

（2）将各辆车的初始出发点置于当前解集中,对每辆车s (s=1,2,...,m),按概率p移至下一地点j,将地点j置于当前解集；

（3）计算各车辆行驶的路径长度Ls(s=1,2,...,m），记录当前的最好解；

（4）按更新方程修改轨迹强度；

（5）nc←nc+1；

（6）nc〈预定的迭代次数且无退化行为(即找到的都是相同解)则转（2）；

（7）目前最好解。

3 实验仿真

参数设置：迭代步数nc≤200；

假设从出发地到目的地途经31座城市，这31座城市加上出发地和目的地都是相互连通的，这31座城市分别编号1，2,3，......,31,它们坐标依次定义如下：

B=[1300 2300；3630 1310；4170 2240；3712 1399；3488 1535；3326 1556；3238 1229；4196 1004；4312 790；4386 570；3007 1970；2562 1756；2788 1491；2381 1676；1332 695；3715 1678；3918 2179；4061 2370；3780 2212；3676 2578；4029 2838；4263 2931；3429 1908；3507 2367；3394 2643；3439 3201；2935 3240；3140 3550；2545 2357；2778 2826；2370 2975]；

利用Matlab对以上述蚁群算法进行仿真结果如图1。

通过算法求得途中这31座城市最优路径为：1，15，14， 12，13，11，23，16，5，6，7，2，4，8，9，10，3，18，17，19，24，25，20，21，22，26，28，27，30，31，29。从上图可以看出当算法迭代次数超过75次后，最优路径长度已经基本保持不变了，求得为1.5590e+004。

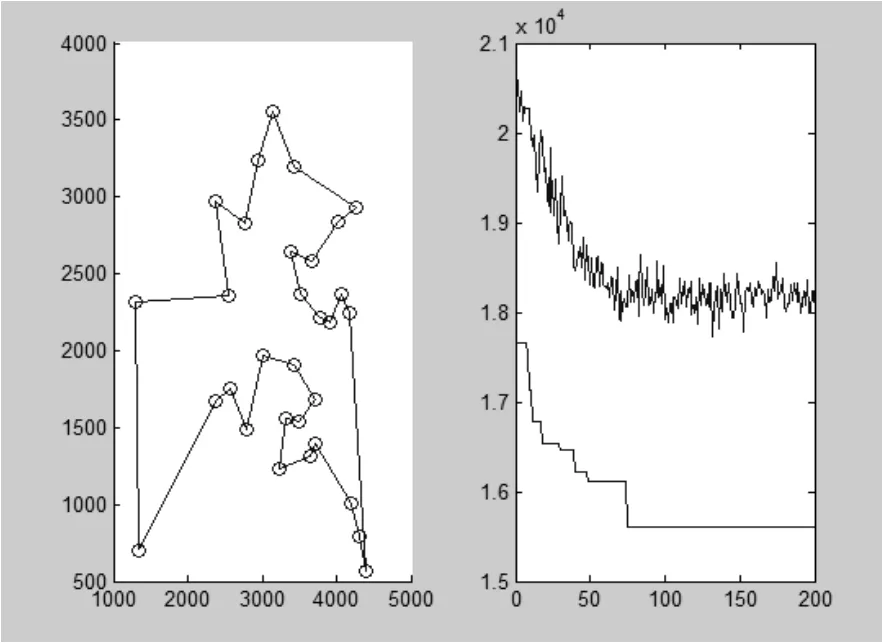
图1 最优路径和迭代次数图

[1]王凌．智能优化算法及其应用[M]．北京：清华大学出版社，2001：195-211．

[2]高国华，沈林成，常文森．求解TSP问题的空间锐化模拟退火算法[J]．自动化学报，1999，25(3)：425-428．

[3]谢胜利，唐敏，董金祥．求解TSP问题的一种改进的遗传算法[J]．计算机工程与应用，2002，38(8)：58-60．

[4]张立明．人工神经网络的模型及其应用[M]．上海：复旦大学出版社，1994：97-98．

Solving Routing Problem of Vehicle Navigation System byAnt Colony Optimization Algorithm

Che Gaofeng Lu Yueran Tan Jun
（College of Information Engineering,Baise University,Baise 533000,Guangxi）

Using the properties of ergodicity,randomicity and regularity of ant colony algorithm,ant colony optimization (ACO)algorithm is analyzed to solve routing problem of vehicle navigation system.Simulation results show that chaos ant colony optimization is a simple and effective algorithm.

ant colony optimization algorithm;vehicle navigation system;routing problem

TP301

A

1008-6609(2015)11-0046-02

车高峰，男，山东烟台人，硕士，讲师，研究方向：现场总线技术、蚁群算法；

*通讯作者：陆月然，男，广西天等人，硕士，副教授，研究方向：物联网。

百色学院一般科研项目，项目编号：2014KB06；广西高校科学技术研究项目，项目编号：KY2015LX388；三亚市院地科技合作项目，项目编号：2013YD56。