基于模糊积分的多分类器融合文本分类研究

邹 晴，钮 焱，李 军

（湖北工业大学计算机学院，湖北 武汉430068）

文本分类的过程主要由以下几个步骤构成:1）预处理，把文本信息表示成结构化信息，以使计算机能够处理；2）特征项选择，使用特征选择算法，从特征集中挑选出最能体现出类别信息的特征项，进而得到最佳特征子集；3）分类器训练与分类运算［1］。其中尤为关键的两步是“特征项选择”和“分类器训练与分类运算”。为了更加高效地解决文本分类问题，在理论上，通过将多个分类器的输出信息结果加以联合来进行最终决策，无疑会是其中一种可行办法。

本文选取BP神经网络、RBF神经网络及采用K-means算法的RBF神经网络，利用Sugeno模糊积分作为融合工具，将多个神经网络文本分类器结合起来，以求得更加理想的中文文本分类结果。

1 神经网络分类器

在分类问题中，分类器占有重要的核心位置，分类器的分类效果取决于分类器的性能。常用的几种分类方法中，在规则比较模糊的判别情况下，人工神经网络方法具有很强的自学性、容错性、鲁棒性、联想记忆和推理意识功能等独特的优势［2］。因此，基于人工神经网络的文本分类方法的改进方法值得研究。神经网络可以看作是一个由函数复合构成的多输入多输出系统，每一个非输入节点都是一个单值多元函数。而通过对这些函数进行模糊积分融合处理，即把几个已经训练好的神经网络分类器同时用于分类，则可以取长补短，获得更好的分类效果。

1.1 BP神经网络分类器

BP神经网络有输入层、隐含层和输出层这三个基本层，其中每个层又都包含若干节点，即神经元，该网络可以看作是非线性的决策过程。起始的特征向量由各特征项的词频分别组成，且各自对应于神经网络输入层的神经元，文本训练在隐含层进行，输出层节点数为输出的文本类别的个数［3］。BP神经网络已经作为人工神经网络中的一种被较多地应用于文本自动分类领域中，其用于函数逼近时，文本特征词的权值的调整采用梯度下降法，存在着局部极小和收敛速度慢等缺点，在一定程度上影响了文本分类的效果。

1.2 RBF神经网络分类器

RBF神经网络即径向基函数（Radical Basis Function）神经网络，在上述BP网络的基础上，在第二层隐含层节点中加入径向基函数作为训练文本的激活函数，对于隐含层的输出加权求和，并据此计算判别特征项的权值，得到从中间层到输出层间的权值。每一个输出神经元都各自对应一个判别函数，所以最大的特征权重判别函数值就是文本分类的结果［4］。RBF网络具有最佳逼近性能和全局最优特性，适于分类曲面复杂的文本分类问题，而且结构简单，训练速度快，得以迅速进行大量运算。可是RBF神经网络对输入特征项有较高要求，若是特征项选择不当或是特征项维数过高的话，神经网络的学习和泛化能力都有出现问题的可能。

1.3 采用K-means算法的RBF神经网络分类器

在RBF网络的基础上，采用K-means算法确定径向基函数的中心，对于给定的待划分的文本类别数k，首先建立一个起始划分。然后为了全部文本特征项的聚类子集当中的记录达到最大相似，且不同文本特征项的聚类子集的记录的差异尽可能的大，运用一种迭代重定位技术，尝试通过对象在划分之间的移动来反复迭代改进划分。而划分出的个体间差异大小选择欧氏距离作为衡量的依据［5］。结合了K-means算法后的神经网络分类文本算法，对于传统的神经网络分类算法收敛速度慢的缺点有所改进，在取得较好分类精度和召回率情况下，具有较高的运算速度和较强的非线性映射能力。

2 基于模糊积分多分类器融合的文本分类

2.1 模糊积分与模糊测度

Sugeno［6］于1974年提出的模糊积分，为信息融合提供了一种可行的方法。首先介绍与模糊积分相关的一些定义及属性。

定义1:设集合X ＝ ｛x1，x2，…，xL｝，其元素有限，其幂集为T（X）。若存在一个集合函数g:T（X）→ ［0，1］满足

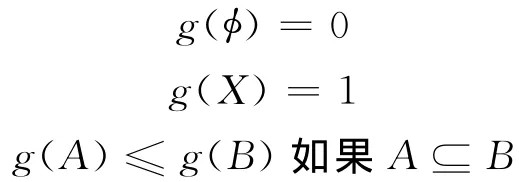
则称其为T（X）上的一个模糊测度。

由模糊测度g的定义可知，存在满足如下属性的模糊测度gλ:对所有A，BT（X）和A∩B＝存在

gλ（A ∪B）＝gλ（A）＋gλ（B）＋λgλ（A）gλ（B），

λ＞－1

1987年日本明尼苏达大学的Kazerooni等人设计了一种直驱式主动柔顺末端操作器，由直流无刷电机带动连杆机构实现平面内二自由度的运动，并通过末端力传感器进行力闭环控制，被动RCC弹簧结构使气动研磨头实现竖直方向的柔顺补偿，如图29所示。为进一步提升末端操作器的柔顺性，Kazerooni联合麻省理工学院开发了被动可调柔顺装置PVCEE(passive variable compliance end-effector)，如图30所示[42]。

令gi＝gλ（｛xi｝），则将映射xi→giλ称为模糊密度函数。

基于模糊测度的概念，Sugeno提出了模糊积分的概念——一个对模糊测度估计的非线性函数。

定义2:设h:X→［0，1］为在X上定义的函数，那么h在集合X上关于模糊测度gλ的Sugeno模糊积分，即

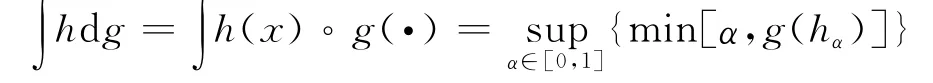
其中，hα是关于h的一个α度量集，hα＝｛x｜h（x）≥α｝。

有限集合X ＝ ｛x1，x2，…，xL｝，设h:1≥h（x1）≥h（x2）≥…≥h（xL）≥0，假如函数h无法满足此关系，则把集合X的元素重新排列直至函数h能够满足此关系为止，那么可以得到在集合X上的关于模糊测度g的函数h的Sugeno模糊积分为

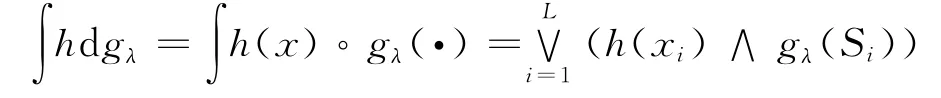
其中，Si＝ ｛x1，x2，…，xi｝。

令g 是一个gλ模糊测度，gi＝g（｛xi｝），则g（Sλi）的值计算如

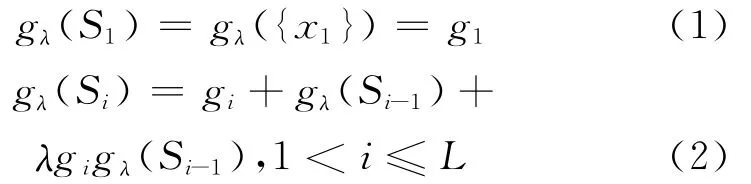
λ由以下等式得出

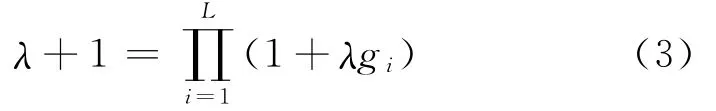
λ∈ （－1，＋∞），λ≠0，且λ唯一。

2.2 基于模糊积分的多神经网络分类器融合

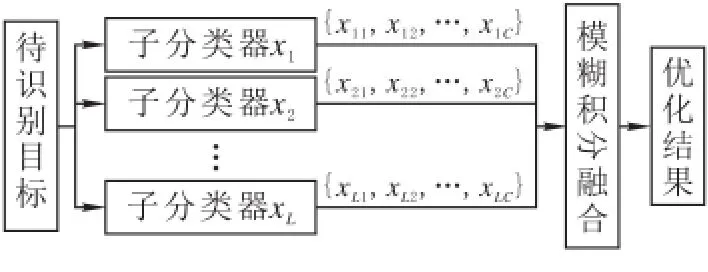
图1 基于模糊积分的多神经网络融合算法

设一共有 L 个子分类器集合 ｛x1，x2，…，xL｝，以及C类目标集合｛y1，y2，…，yC｝。对于某待识别目标s，其被判定为各类目标的置信度，即是由子分类器xi输出的识别结果Ui（s）＝ ［μi1（s），μi2（s），…，μiC（s）］。通过Sugeno模糊积分进行融合时，集合X代表这L个子分类器，令网络xi将示例S分为第j类的概率为hj（xi）＝μij，gj（Si）为示例S被子分类器集Si识别为第j类的重要性，经过Sugeno模糊积分融合后，目标s属于第j类目标的概率也就是置信度，即

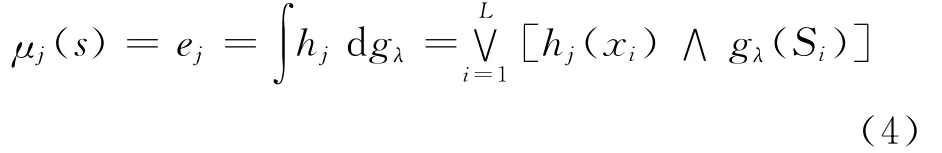
依照最大隶属原则，如果系统要求输出某一目标类别，就输出最大μij（s）对应的目标类别［7］。

为将各子分类器输出的距离dij（s）转换成置信度，可采用

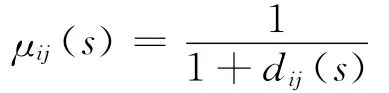
模糊积分分类器融合识别的过程如下:

1）利用式（3）算出λ；

2）将s属于各类的信度从小到大依序排列，并将相应的模糊密度也重新排列；

3）使用式（1）、（2）进行模糊测度的计算；4）通过式（4）计算模糊积分；

5）最后按最大隶属原则进行分类。

2.3 基于模糊积分的多神经网络分类器融合的文本分类

实验中以10个类别的文本为样例s，分别为:环境（30篇）、计算机（40篇）、交通（36篇）、教育（34篇）、经济（50篇）、军事（40篇）、体育（48篇）、医药（42篇）、艺术（54篇）和政治（26篇）共400篇文章作为训练集。对每个类别，分别统计出现在类中的词频，互信息及类别信息，并且将根据这三个特征计算出的类别相关度，根据权重的大小，进行排序。

在关键字个数为20的情况下，分别用BP神经网络分类器、RBF神经网络分类器、采用 K-means算法的RBF神经网络分类器和基于模糊积分的多神经网络融合分类器这四种分类器根据输出的距离dij（s），将文本分为目标的10个类别，进行训练测试比较。

首先，采用某种方法［8］对10个类别分别得到相应的模糊测度gλ。

在本实验中，L＝3，带入式（3），即

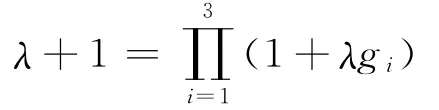
整理得

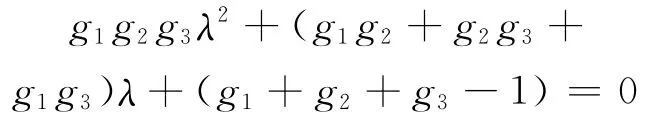
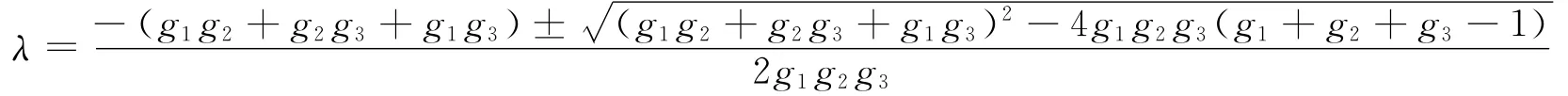
根据文献［8］结论，及根与系数的关系有以计算机、经济、艺术三类为例，分别得到相应的gλ模糊测度。根据文献［9］，假设各类相应的g1，g2，g3取值，及其经过推导后结果见表1。

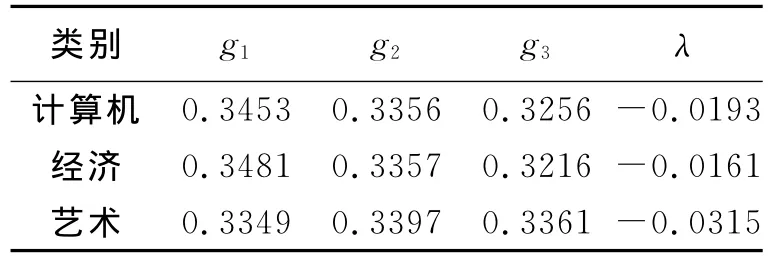
表1 模糊密度和相应的λ

根据式（1）（2）计算模糊测度，有

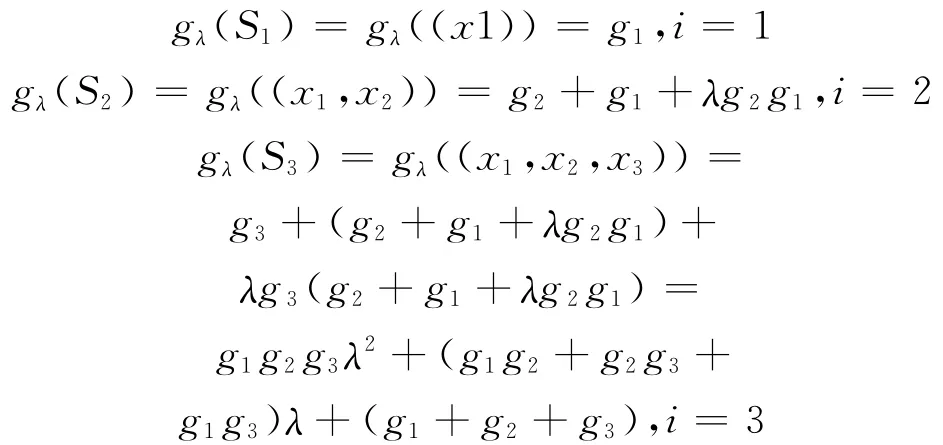
以查准率为例，结合表2已知子分类器数据，按顺序排列后再由式（4）进行模糊积分，有

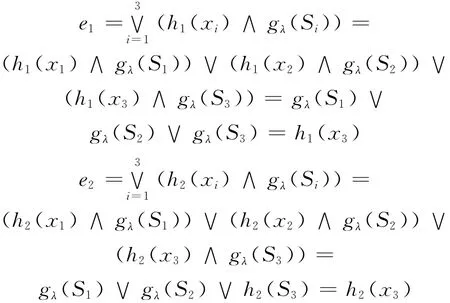
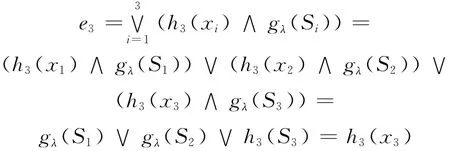
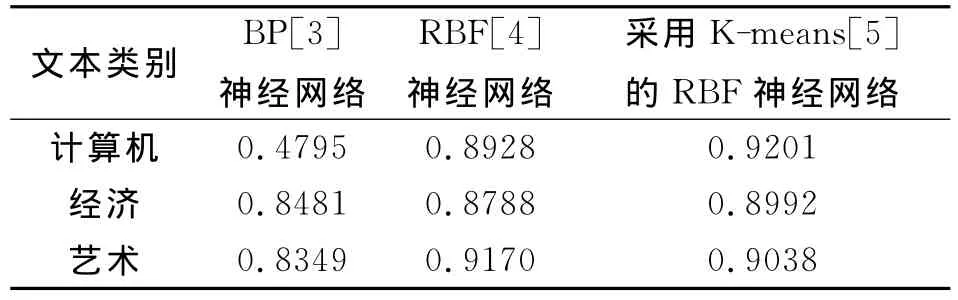
表2 三种不同神经网络查准率

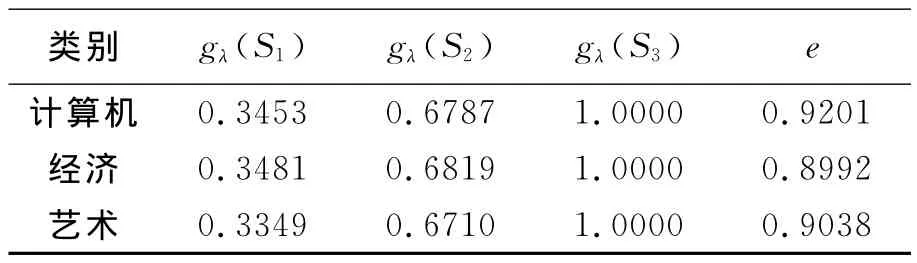
表3 gλ模糊密度与模糊积分e

3 实验结果与分析

3.1 评价标准

查准率是所有判断出的文本数和人工分类结果的文本数一致的文本所占的百分比［10］。数学公式如

查全率是文本分类系统实际识别出的准确结果和与文本测试集中总的准确结果的百分比。数学公式如查准率和查全率都必须考虑，不能忽视，因为这两者反映了文本分类质量的两个不同面，所以出现了一个新的评价指标的测试值:

3.2 测试结果

以计算机类文章的分类为例，最终测试结果见表4。

表4 计算机类文本的不同方法测试结果比较

从表4中可以看到，各子分类器在文本分类上的表现各有优劣。准确度（包括查全率、查准率及F1值）在用模糊积分融合后的多分类器的分类结果，比起各子分类器，优化效果明显。

4 总结

在神经网络文本分类器与模糊积分的基础上，提出一种基于模糊积分的多分类器融合的中文文本分类方法，不同子分类器的融合，使查准率得到有效提高，进而证明了其有效性与实用性。由于各子分类器间的互补性因融合系统的性能得到了提高，因此，即使某一分类器对某类目标的识别率不高，也不会影响该融合系统的性能。实验结果表明，该方法有效可行，且具有更好的分类结果。

［1］ 陈艳秋，孙培立.一种基于类别强信息特征和贝叶斯算法的中文文本分类器［J］.计算机应用与软件，2014（08）:330-333.

［2］ 丁 硕，常晓恒.Gaussian型RBF神经网络的函数逼近仿真研究［J］.河南科学，2013（09）:367-369.

［3］ 朱 敏.基于自适应遗传BP神经网络的文本分类方法研究［D］.南昌:南昌大学，2010.

［4］ 郁婵娴.基于RBF网络的中文文本自动分类的研究［D］.上海:华东师范大学，2007.

［5］ 卢曼丽.基于K-means算法的神经网络文本分类算法研究［J］.中国管理信息化，2014（21）:80-82.

［6］ Surgeno M.Fuzzy measures and fuzzy integrals:A Survey［C］.Fuzzy Automata and Decision Processes msterdam:North Holland，1977:89-102.

［7］ 程 剑，应自炉，张有为.基于模糊积分多分类器融合的人脸表情识别［J］.信号处理，2005（21）:358-361.

［8］ 陈俊芬.基于Choquet模糊积分的多神经网络融合模型［D］.保定:河北大学，2005.

［9］ 王熙照.模糊测度和模糊积分及在分类技术中的应用［M］.北京:科学出版社，2008:206.

［10］薛 亮.基于SVM的中文文本分类系统的设计与实现［D］.重庆:重庆大学，2012.