超级电容器串联分组均压法的设计与仿真

杨泽明，王 超，张小华，郑 浪

（湖北工业大学电气与电子工程学院，湖北 武汉430068）

超级电容器［1－3］串联组件电压均衡技术主要有基于能量消耗型技术的稳压管串联均压法、开关电阻串联均压法，以及基于能量转移型技术的单飞渡电容器串联均压法、多飞渡电容器串联均压法、电感储能串联均压法等多种方法［4］。本设计旨在利用SIMULINK软件，重点对基于能量消耗型的稳压管串联均压法和基于能量转移型的电感串联均压法进行分析与仿真，并在此基础上提出串联分组均压法实现两级均压控制。考虑到超级电容器充电过程中电压收敛性的要求，第一级采用电感串联法，第二级采用稳压管法，再通过仿真验证其可行性和效果。

1 超级电容器等效电路模型的建立及参数确定

1.1 超级电容器的等效模型建立

在诸多生产研究超级电容器的大型厂家中，美国的Maxwell生产的产品在市场上的占有率相对较高［5］，故本设计选取 Maxwell公司的相关产品。因其公司生产的D单元系列主要在电力备用电源及可再生能源系统中应用较广泛，故拟采取该系列的产品作为研究对象。D单元系列有两款产品，分别是BCAP0310和BCAP0350。相对于BCAP0350，BCAP0310拥有较小的内阻以及更高的功率系数，储能效果更加突出。故选用BCAP0310为研究对象。

研究对象确定以后，建立其等效电路模型。之前对超级电容器的特性研究一般常用的等效电路模型是串联RC电路模型（图1）。

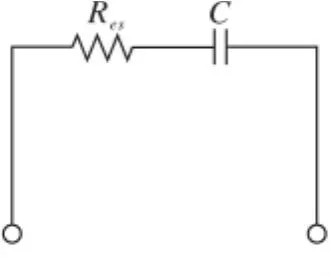
图1 超级电容器的串联RC模型

图1 中，C为超级电容器的理想定容，Res为超级电容器的等效串联电阻。C表示超级电容器的储存电荷的能力，Res表示超级电容器在充电过程中内部发热所消耗的能量以及在放电过程中超级电容器两端随着放电电流大小变化而变化的端电压的大小。该模型结构简单，分析方便，但是漏电流效应却没有表现出来。现在的研究方向是在该模型的基础上进行改进［6］，一般是在理想电容上并联一个表示超级电容器漏电流效应的等效并联电阻Rep，改进模型结构见图2。

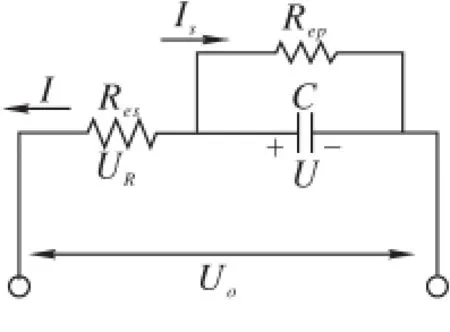
图2 超级电容器等效电路模型

并联电阻Rep的引入能够很好地反映超级电容器的静态特性即其长期储能的性能优劣，从理论上来说以此作为超级电容器的等效模型可以得到较为准确的仿真结果。

1.2 等效电路模型的参数确定

由BCAP0310超级电容器参数可知，其理想电容值C为310F，等效串联电阻Res为2.2mΩ，现在只需要确定等效并联电阻Rep。

由图2可知，超级电容器两端电压

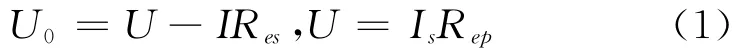
超级电容器放电功率

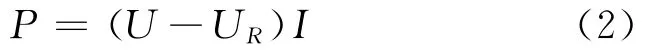
其中U0为超级电容器端电压；U为理想电容器电压；UR为等效串联内阻Res上电压；I为放电电流，Is为漏电电流。

1）超级电容器容量C和实际储存电量Q，超级电容器容量C，根据超级电容器容量定义计算:

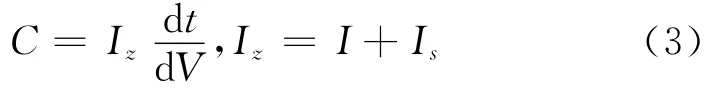
设第n时刻超级电容器储存的电量为Q（n），则第n＋1时刻超级电容器储存的电量Q（n＋1）满足

2）超级电容器工作电压V。设某时刻超级电容器的工作电压为V（n），下一时刻为V（n＋1），则有

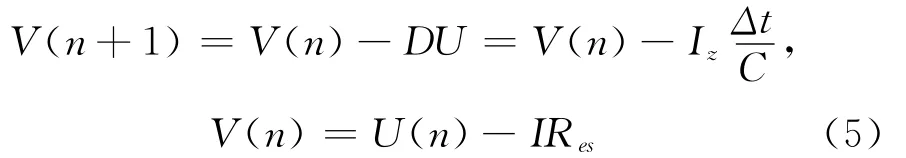
其中U（n）为与V（n）相对应的理想电容电压值。

综合式（1）至式（5）可得:超级电容器电流放电过程中，该超级电容器端电压变化满足

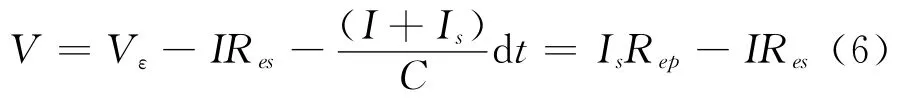
其中V为某一时刻超级电容器端电压，Vε为超级电容器额定电压，I为放电电流，Is为漏电流，C为理想电容值，Res为超级电容器等效串联电阻。

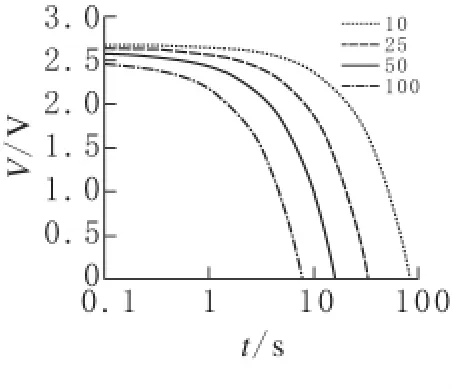
图3 超级电容器放电曲线

等效并联电阻Rep的确定，通过式（6）和图3所示的单体超级电容器的放电曲线来得到结果。Vε为超级电容器单体额定电压，本设计中该值为2.7V，串联电阻Res的取值为2.2mΩ，最大漏电流Is为0.45mA。由式（5）可知超级电容器漏电流的最大值在图3所示的超级电容器电流放电曲线初始处。这样在图3中，选取放电电流为10A的曲线为研究对象，结合式（6）及相关数据可得超级电容器单体等效并联电阻为6 000Ω左右，故在本设计中将其设定为6 000Ω。

2 超级电容器串联均压控制方法的仿真分析

超级电容器串联均压技术一般可以按照超级电容器串联电路在运行过程中均压部分能量的损耗情况来分为两大类［7，8］:

1）能量消耗型均压技术。在每个超级电容器单体上并联一个电阻或稳压器等耗能元件将端电压较高的超级电容器单体中的多余能量以发热的形式消耗掉，从而使各个单体电压达到一定值后趋向均衡均压。此技术主要有稳压管串联法、并联电阻串联法、开关电阻串联法等。该技术的均压电路结构简单、成本小，但是在均压过程中大量能量以热能的形式消耗掉，发热能量过高会影响整个均压电路的元件性能，一般在能量利用效率不高的场合应用此均压方法。

2）能量转移型均压技术。在超级电容器串联组件中接入部分电感、电容等暂时储能元件，将端电压较高的超级电容器单体中的能量转到端电压低处，从而达到均压的效果。此技术有开关电容串联法、电感串联法等。相对于第一类均压方法来说，该方法拥有均压速度快以及均压耗能少的特点，但该类方法需要在均压的过程中实时获取每个单体端电压，将能量从电压高处转移到电压低处，这样均压电路中就需加入采样比较元件来控制均压电路中相关能量转移元件的接入与移除，从而使得电路结构变得复杂。

下面主要对稳压管串联均压法和电感串联均压法做仿真分析，其电路结构见图4和5，电感串联法的结构中省去了实时电压测量及比较单元。

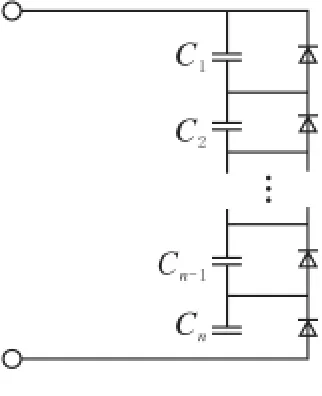
图4 稳压管串联法

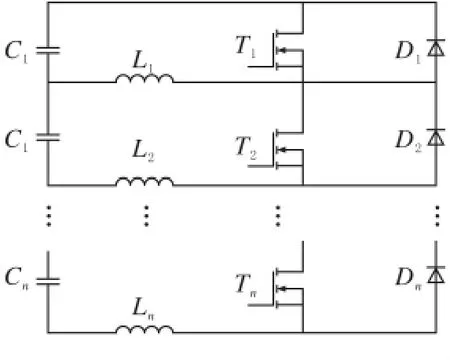
图5 电感串联法

考虑到单体超级电容器BCAP0310的单体额定电压只有2.7V，实际使用时需要串联几十个或几百个才能满足电压要求，由于只是对现有串联均压方法的均压效果进行分析研究，仿真时对于结构简单的稳压管法使用6个单体，对于复杂的电感串联法使用3个单体。首先对没有采取任何均压措施的超级电容器串联组件充电电路进行仿真（图6）。电容的额定值为310F，考虑额定电容值在－10%～＋10%之间波动，则图6中的C1－C6的值为280F、289F、298F、307F、316F、325F，串联电阻R1－R6为2.2mΩ，并联电阻为6 000Ω，直流充电电源为50A，因SIMULINK模块中没有直流电源，可以把交流电源相位设置为90°，频率为0Hz实现直流电源功能。图7为充电过程中各个超级电容器单体端电压变化曲线。

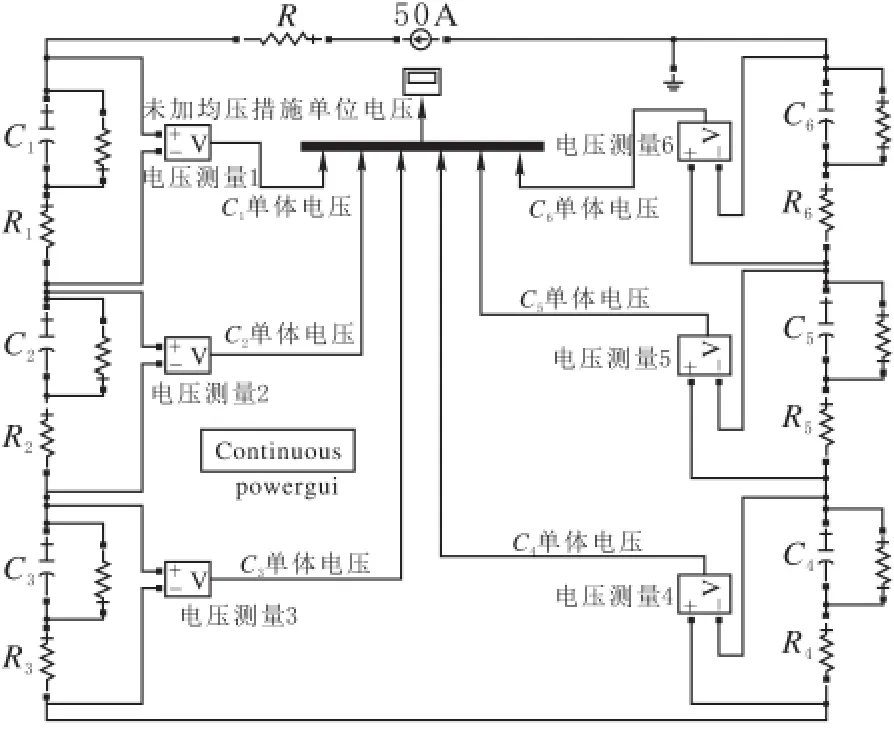
图6 超级电容串联电路

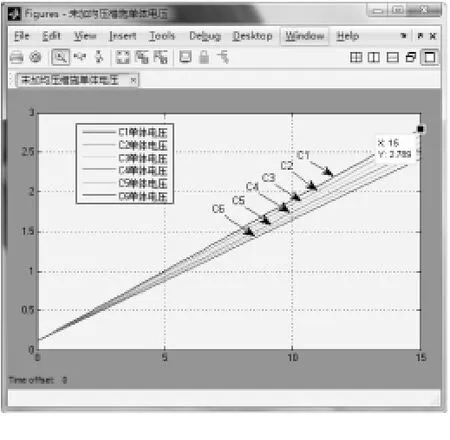
图7 未加均压措施的串联电路充电曲线

图7 中曲线由上到下依次为C1－C6所代表的单体充电电压变化曲线，可以看出电容低的单体端电压一直高于电容高的单体端电压。当充电过程结束之后，单体电容值最低的单体电压达到2.8V时，电容值最高的单体端电压仅为2.4V。而且其他的单体端电压均未达到额定电压值，大部分单体都没有达到最大储能，造成了超级电容器的浪费。图6中，当单体电容值都相等，而等效串联电阻呈现一定的分散性时，R1－R6的阻值分别为2.12mΩ、2.14 mΩ、2.16mΩ、2.18mΩ、2.2mΩ、2.22mΩ 时，各单体充电端电压的变化曲线见图8，充电曲线前半段的放大图见图9。

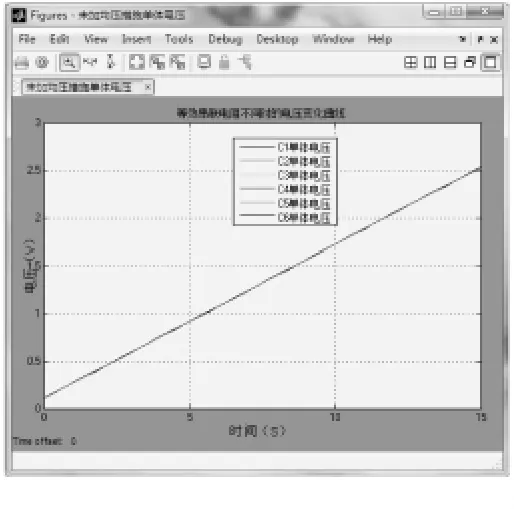
图8 等效串联电阻不同时的充电曲线

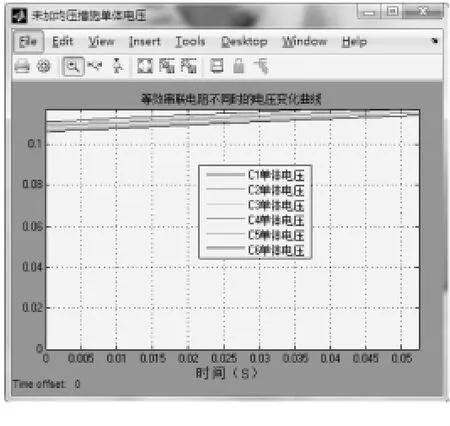
图9 等效串联电阻不同时的充电曲线前半段

由图8和图9知，若串联单体的等效串联电阻阻值不同时，充电曲线拥有近似相同的斜率，而且在充电结束时各个单体的稳定电压相差极小。这说明超级电容器电容的分散性对超级电容器串联时各个单体电压变化的影响远大于等效串联电阻的分散性的影响。基于此，在下面的仿真中，仅考虑超级电容器单体电容的分散性对串联均压过程的影响。

在稳压管串联均压仿真中，设置C1－C6的电容值为280F、289F、298F、307F、316F、325F，等效串联电阻R1－R6值为2.2mΩ，等效并联电阻值为6 000Ω，同时设置稳压管的反向击穿电压低于超级电容器单体电压2.7V，这里设置为2.5V，图10为稳压管串联均压电路。

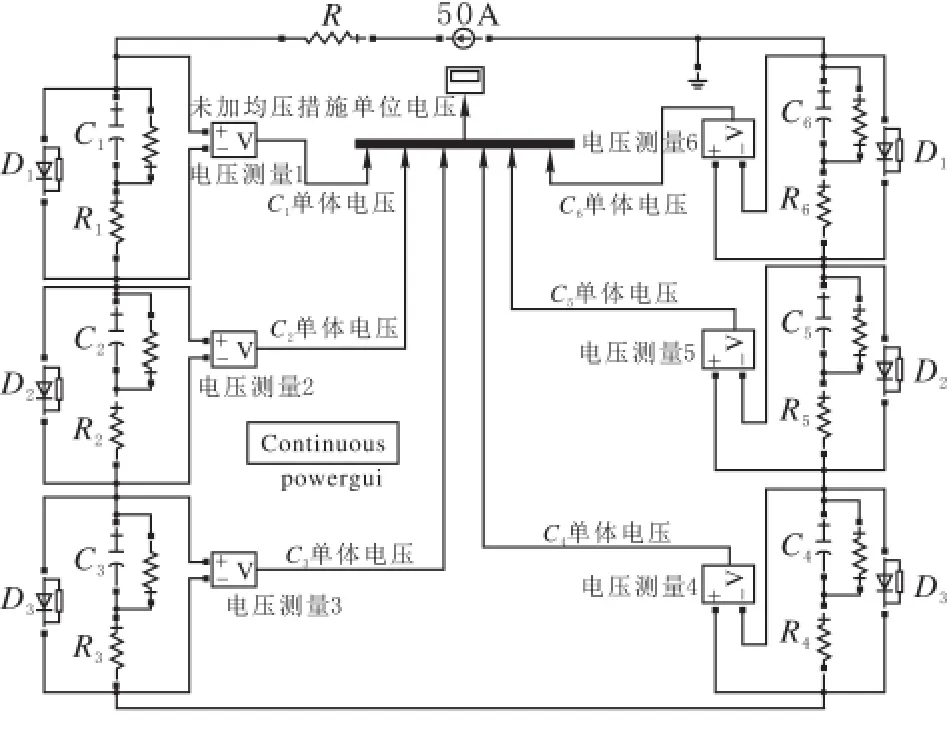
图10 稳压管串联均压电路

由图11可知，当第一个超级电容器单体C1（即电容最小的超级电容器）的端电压超过稳压管的反向击穿电压时，其电压增长速度明显减小，近似于0，此时其他的超级电容器单体端电压还未到稳压管的反向击穿电压，其端电压与C1的端电压相差还较大，但随着充电时间的增加，每个单体所并联的稳压管都被反向击穿，从而使得每个超级电容器单体电压均稳定在2.549V左右，差值很小。可以看出经过一定的时间，稳压管串联均压法能够将串联均压电路中的所有超级电容器单体端电压均控制在稍高于稳压管反向击穿电压的某值，具有较好的串联均压效果。但同时也可以看到，从第一个超级电容器单体所并联的稳压管被反向击穿到最后一个被击穿，中间需要很长的一段时间。稳压管被击穿之后，单体端电压也需要一定的时间才能趋于稳定，造成稳压管消耗大量的能量。

在电感串联均压仿真中，需要注意的是均压电路中电感接入开关的动作控制单元的设计。该单元需要实时检测串联电路中各个单体端电压，并找出端电压最高的超级电容器单体，然后控制旁路开关的动作，实现能量转移的任务。由于基于电感串联均压法而设计的均压电路相对较为复杂，这里只采用3个单体进行电感串联均压仿真（图12）。

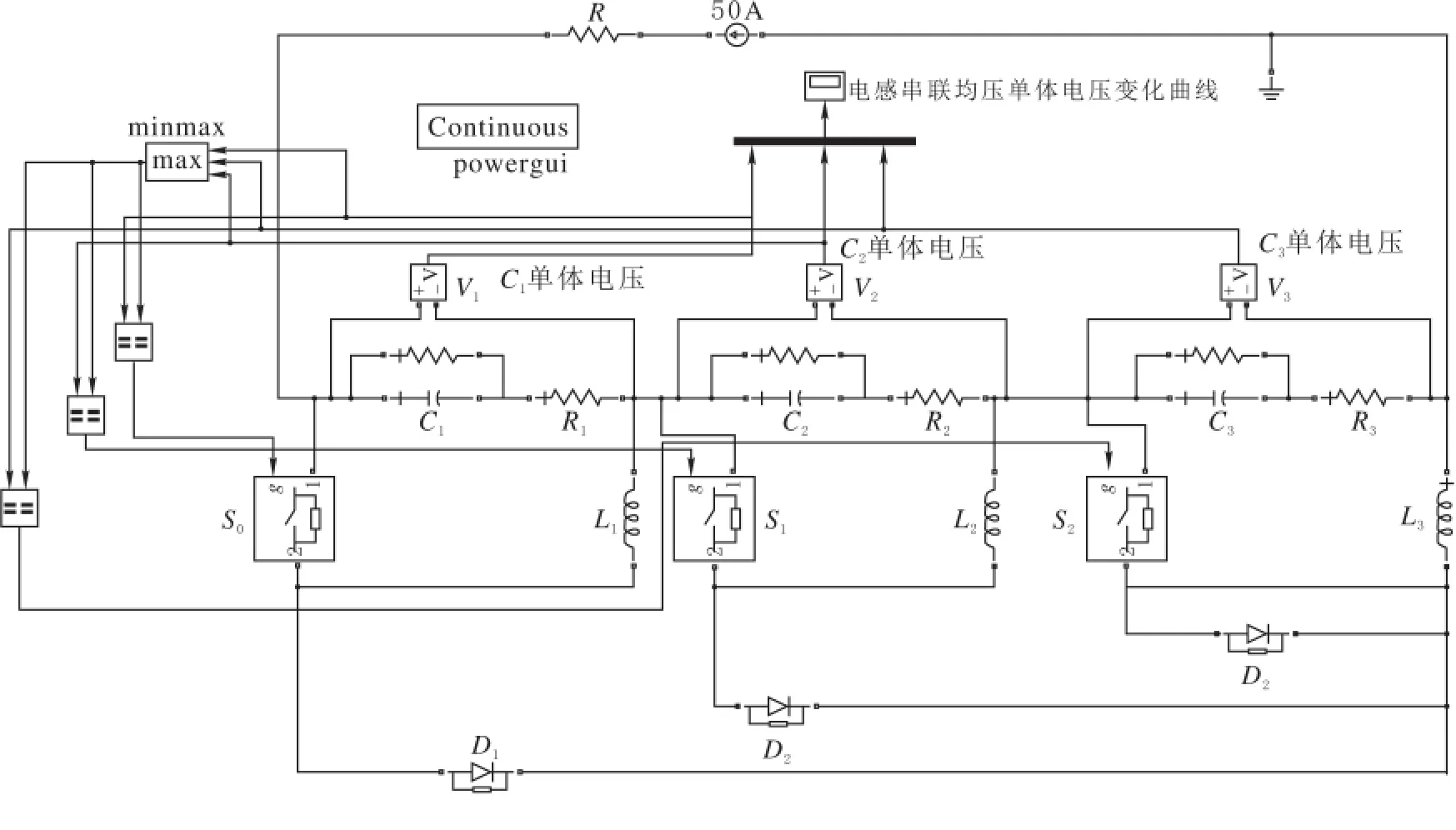
图12 电感串联均压电路

图12 中C1＝280F，C2＝300F，C3＝320F，L1＝L2＝L3＝2.5H。其中的取极值（MinMax）单元及三个比较运算（Relational Operator）单元组成电感接入开关的动作控制单元。通过实时检测出串联电路中端电压最高的超级电容器单体，并产生相应的控制信号，将其旁路开关闭合，接入电感，使一部分能量转移到该电感中。当其他单体端电压超过该单体端电压成为最高电压时，则该单体旁路开关断开，将电感中存储的能量通过二极管释放到其他的超级电容器单体中，而此时端电压最高的超级电容器单体也会将其一部分能量转移至与其相连的电感中，以备之后的能量转移。

由图13和14对比可知，在充电结束后，未采用电感串联均压法的超级电容串联电路中，各个单体稳定电压的差值明显大于采用了电感串联均压法的稳定电压差值，表明电感串联均压法拥有较好的电压均衡效果。

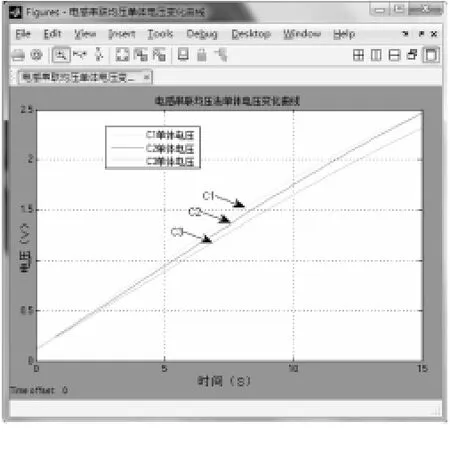
图13 电感串联均压电路充电曲线

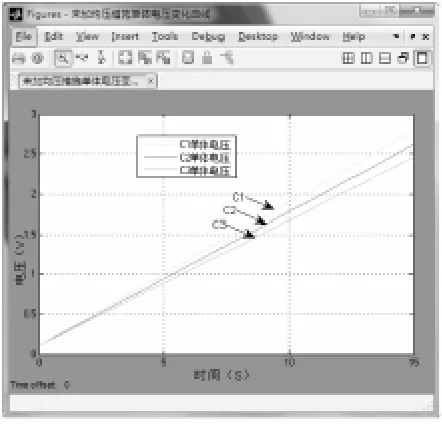
图14 未采用均压措施的串联充电曲线

3 超级电容器串联分组均压方法的设计与仿真

当超级电容器单体个数超过10个以上，采用一般的串联均压法会出现均压时间过长、均压精度降低等问题。由此提出一种串联分组均压法来解决这一问题。采用两级均压控制，第一级采用电感串联均压法，第二级采用稳压管法，图15为其电路结构。

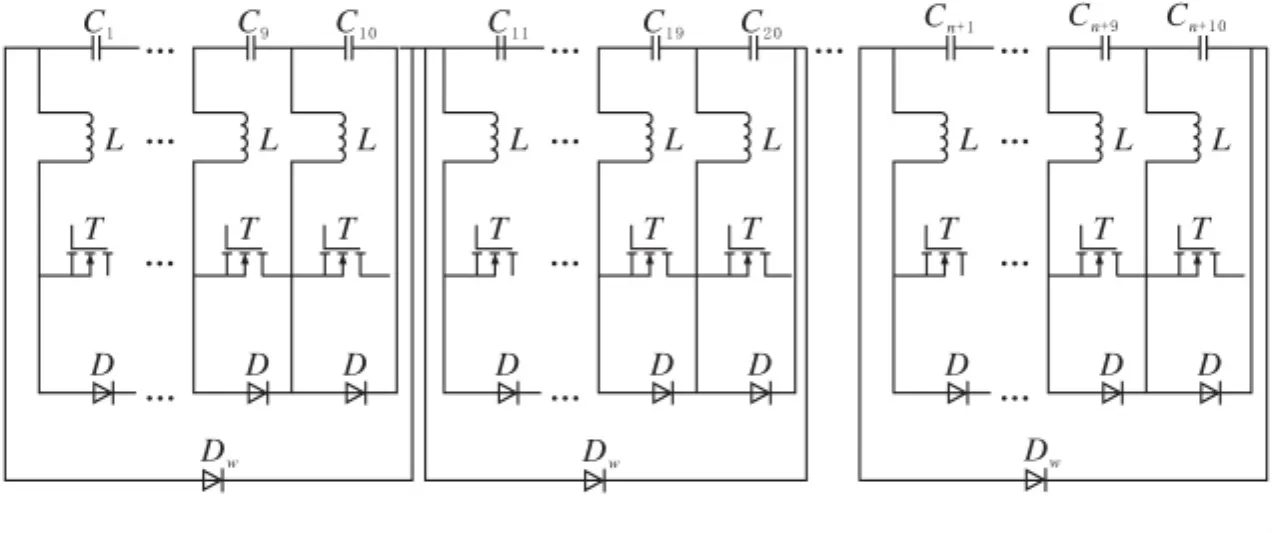
图15 电感串联均压法与稳压管法的分组均压方法结构图

在仿真时选取4个单体超级电容器，分成两组，每两个单体为一组。图16为电感串联与稳压管均压法的仿真图。在图16中C1－C4的电容值分别为280F、300F、320F、340F，旁路电感L1－L4均为2.5H，二级均压元件稳压管DW1和DW2的反向击穿电压均设置为5V。

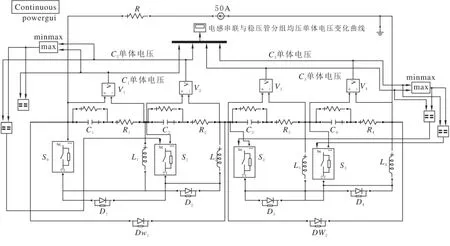
图16 电感串联均压法与稳压管法的分组均压法电路仿真图

图17为采用分组均压法后各单体电压的充电曲线，与图13相比，充电结束后各单体端电压之间差距减小了许多，各单体端电压基本稳定在2.5V左右，而图13中的各单体端电压之间的差距还很大，形成鲜明对比。与图11相比较，采用分组均压法在16s左右串联电路中各单体电容的端电压值基本保持稳定，而图11则需要18s左右，这说明分组均压法可以减少均压时间，另外还可以看出图17在充电结束后的稳定值为2.5111V，图11中的稳定值为2.549V，这表明分组均压法拥有更高均压精度。由此可以看出，以稳压管法作为二级均压手段的基于电感串联均压方法的分组均压方法相对于单纯的均压方法来说，拥有更好的均压效果。

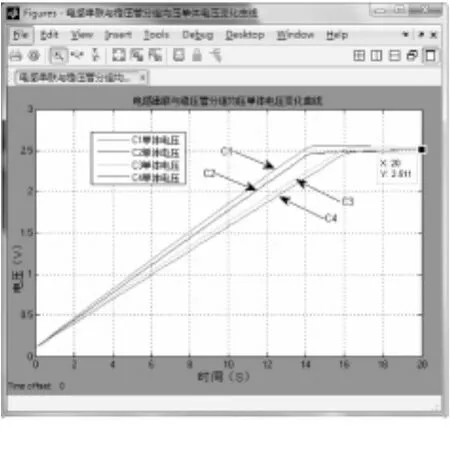
图17 电感串联均压法与稳压管法的分组均压法充电去曲线

4 结束语

针对超级电容器的串联均压不平衡的问题，在对现有超级电容器串联均压方法分析与仿真的基础上，提出了一种新的串联均压方法——超级电容器串联分组均压法。采用两级均压控制，可以将各单体端电压更好的稳定在额定电压附近。第一级均压为基于能量转移型的电感串联均压法，第二级均压为具有电压收敛性的稳压管法，经过仿真实验验证，该方法比单纯的串联均压法拥有更好的均压效果，是一种优良的改进方法，值得进一步的研究。

［1］ 朱修锋，景晓燕，张密林.金属氧化物超级电容及其应用研究进展［J］.功能材料与器件学报，2002，8（03）:325-330.

［2］ 袁国辉.电化学电容器［M］.北京:化学工业出版社，2006.

［3］ 张治安，邓梅根，胡永达，等.电化学电容器的特点及应用［J］.电子元件与材料，2003，22（11）:1-5.

［4］ 刘兴江，陈 梅，胡树清，等.电化学混合电容器的研究进展［J］.电源技术，2005，29（12）:787-790.

［5］ 李海东.超级电容器模块化技术的研究［D］.北京:中国科学院电工研究所，2006.

［6］ 盖晓东，杨世彦，雷 磊，等.改进的超级电容建模方法［J］.北京航空航天大学学报，2010，36（02）:172-175.

［7］ 祁新春，李海冬，齐智平.双电层电容器电压均衡技术综述［J］.高电压技术，2008，34（02）:293-296.

［8］ Marie-Francoise J-N，Gualous H，Berthon A.Super capacitor thermal and electrical behavior modeling using ANN［J］.Electric Power Applications，2006（03）:255-262.

［9］ 李海冬，冯之钱，齐智平.一种新颖的串联超级电容器组的电压均衡方法［J］.电源技术，2006，30（06）:499-503.

［10］刘小宝，许爱国，谢少军.串联电容器组电压均衡研究［J］.电力电子技术，2009，43（03）:48-50.