一种含噪投影的螺旋锥束CTKatsevich重建算法

惠苗

（三明学院信息工程学院，福建三明365004）

一种含噪投影的螺旋锥束CTKatsevich重建算法

惠苗

（三明学院信息工程学院，福建三明365004）

在实际工程应用中，投影体数据含有大量噪声.Katsevich算法作为一种精确的重建算法，它可以得到质量较高的重建图像，但它需要对投影数据旋转角和二维探测器坐标做求导运算，求导会放大噪声，甚至使重建图像失真.结合Katsevich算法中对投影数据的旋转角避开求导和探测器坐标求导采用五点差分方法代替直接求导，可以降低对旋转角度的采样率，减少对病人的射线辐射和射线成本，减小求导误差和噪声带来的负面影响，从而提高图像质量.

螺旋锥束CT；图像重建；Katsevich算法；投影数据求导

CT作为一种先进的无损检测技术，已广泛应用于医学、考古、航空航天、安全检测、农业、设备制造等相关领域.其中，CT的扫描方式和重建算法是CT研究的关键技术和研究热点.在扫描方式上，目前主要应用的有圆形扫描和螺旋扫描两种，对于长物体采用螺旋扫描方式有明显的优势，螺旋扫描时间短、射线利用率高、轴向分辨率高，而且它的扫描轨迹满足三维精确重建的完全条件.在重建算法上，Katsevich算法是一种精确的重建算法，该算法重建图像的质量较高[1-3]，但该算法在重建的过程中，需要对投影数据求导，求导过程会放大噪声，影响图像的边缘信息，甚至使重建图像失真.针对这种问题，本文结合了避开对投影数据旋转角求导和对探测器求导采用五点差分方法求导.

1 螺旋锥束扫描方式

射线源扫描轨迹描述为：

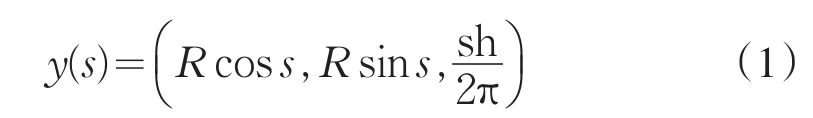
式中R为射线源到物体中心的距离，也称为旋转半径，h为螺距，s为旋转角度.

感兴趣区域重建坐标点定义为X=(x,y,z),待重建图像在点 X的函数值表示为 f(X),区域x2+y2＜R称为视场FOV（fieldofview）.在旋转角s确定下，X点在探测器上投影的位置表示为(u,v)，投影数据值表示为g(s,u,v).

定义3个两两垂直的单位向量d1,d2,d3，用来表示平板探测器上锥束投影测量的局部坐标系，这里 d1=(-sins,coss,0),d2=(0,0,1),d3=(-coss,-sins,0).

如图1所示，射线源y(s)在平板探测器上的投影点是平板探测器的坐标原点O,物体上任意点X投影为平板探测器上的坐标记为(u,v).

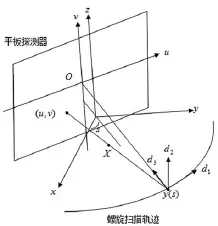
图1 平板探测器上锥束投影测量的局部坐标系图

2 Katsevich重建算法

根据Katsevich螺旋锥束CT的算法框架[4]，视场内的点X处的函数灰度值 f(X)可通过点X的通过PI线段确定的螺旋轨道区间上的投影数据进行滤波运算，再经过加权反投影得到.重建公式可写为：

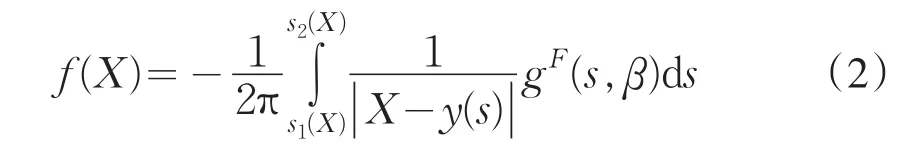
这里滤波数据可由下式确定：

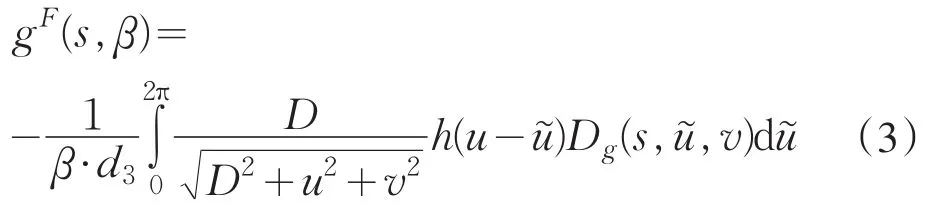
式中，D为射线源到探测器平面中心的距离；h表示 Hilbert变 换 核 函 数 ，定 义 为 ：h(t)=表示对投影数据g(s,u,v)求导运算.

螺旋锥束Katsevich算法的实现过程分为投影数据求导、滤波、反投影重建三部分.

（I）投影数据求导：

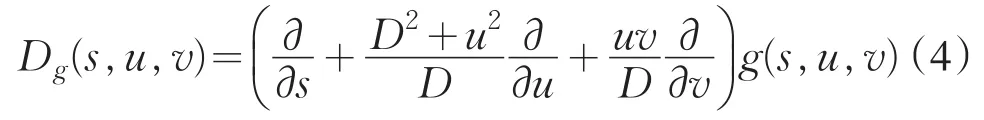
（II）求导后的数据进行希尔伯特变换：

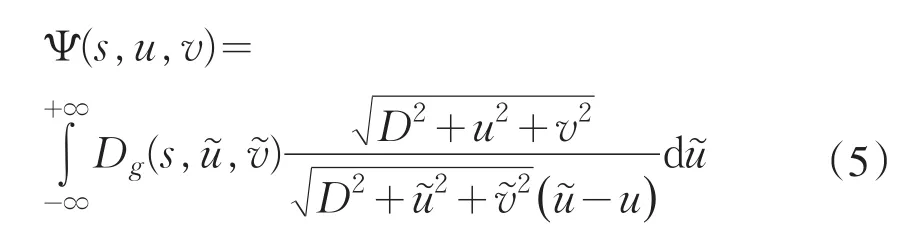
（III）反投影重建：

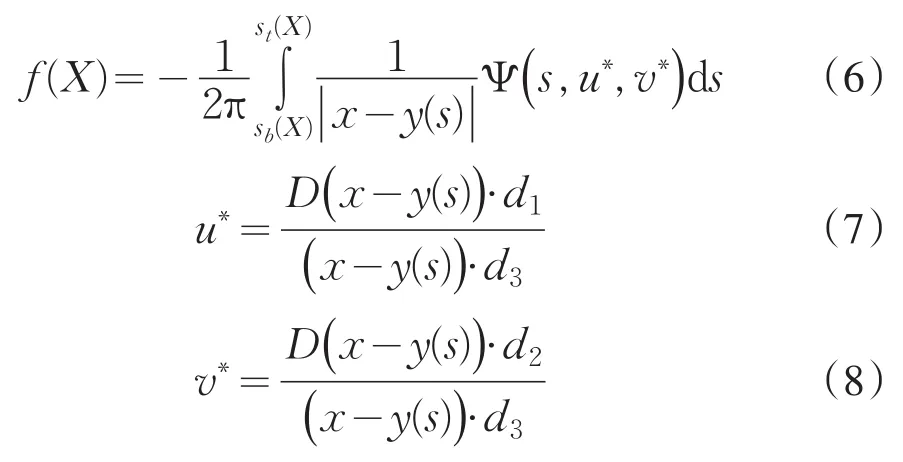
其中sb(X)、st(X)表示由X点所确定的PI线的两个端点.

3 Katsevich重建算法回避投影角度求导

在式（4）的计算中，需要沿着旋转轨道对投影数据g(s,u,v)进行求导运算，然而在数值计算中求导数运算是通过差分运算来逼近的，这使得求导运算依赖于旋转角度的采样率和探测器单元的采样率.其中螺旋旋转角的采样率远低于探测器单元的采样率，而且螺旋旋转角的采样率越高，在医学上病人射线辐射就越高，射线成本就越高，运算量也很大.所以，考虑Katsevich的重建公式中避开对旋转角度的求导，这将在医学临床有极其重要的意义[5-6].式(9)给出了避开旋转角求导的重建公式.

式中：

实际的螺旋锥束成像系统中，随着探测器的发展和采样率逐步提高，使得投影数据对探测器变量u和v的数值求导运算精度远高于投影数据对旋转角的求导运算，因此重建公式通过数学上的变形，避开了旋转角度的求导运算，这具有重要的实际意义.

4 投影数据的五点方法求导

螺旋锥束Katsevich算法的实现过程，需要对投影数据求导，有多项式拟合求导[7]，求导过程较复杂，本文采用五点差分方式求导，可以有效增强图像边缘.下面公式是投影数据对探测器u和v求导，其中定义旋转角度采样间隔为Δs,采样数为K,每个探测器单元的宽度为Δu,探测的宽度数量为M,每个探测器单元的高度为Δv,探测器的高度数量为N,探测器的宽为M·Δu,探测器高为N·Δv,投影数据离散形式为 g(sk,um,vn)，这里 0≤k≤K-1，0≤m≤M-1，0≤n≤N-1.投影数据g(sk,um,vn)避开对旋转角度的求导，对探测器横向单元求导如下：

当m=0时：

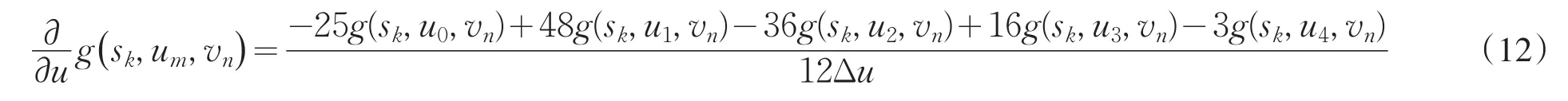
当m=1时：

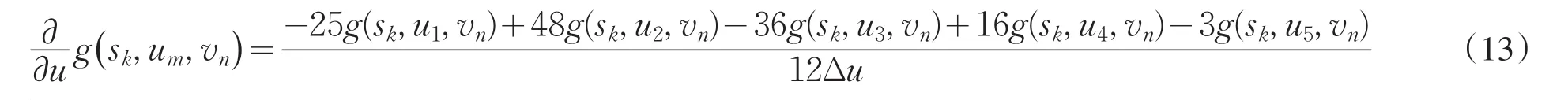
当1＜m＜M-2时：

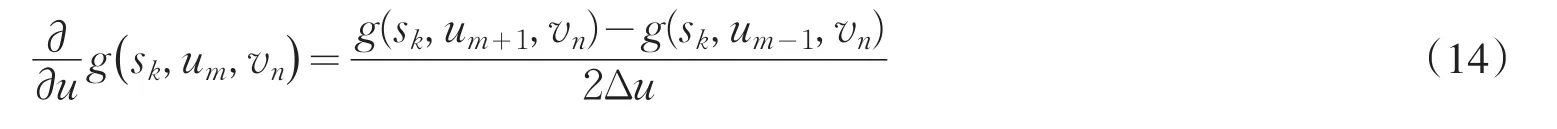
当m=M-1时：

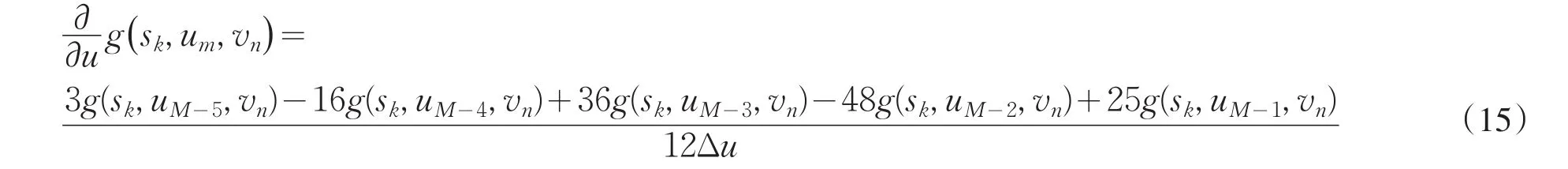
当m=M-2时：

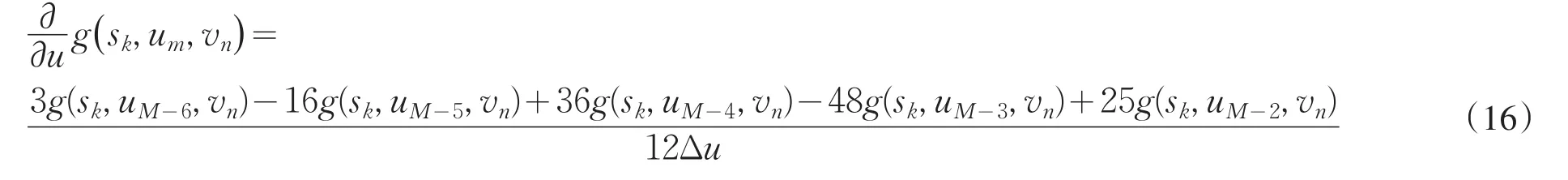
同理，可得投影数据g(sk,um,vn)对探测器纵向单元求导.

实际采集的投影数据中，由于CT探测系统噪声包括暗电流噪声、散粒噪声、热噪声等[8]，而热噪声和散粒噪声是高斯白噪声，这些噪声会弱化边缘信息，如果通过直接求导可以放大噪声信息，而利用五点公式求导可以减少求导误差，增强边缘信息，减少噪声对重建图像质量的影响.

5 实验数据及重建结果

5.1 实验数据

为验证以上算法有效性，对修订的三维Shepp-Logan头部模型利用解析法生成螺旋锥束投影数据，并对螺旋锥束投影数据添加高斯白噪声，利用改进的求导方法和改进Katsevich重建方法锥束对Shepp-Logan头部模型进行重建，射线源到探测器的距离D为150像素，螺旋扫描轨迹的螺距为25像素，探测器的高和宽都为100像素，每圈采样360次.

5.2 重建结果

以经典Shepp-Logan头部模型为例，在实验中添加高斯白噪声，因为在CT探测系统中，噪声主要成分有低频噪声与白噪声[5].不仅通过实验用原始Katsevich重建算法重建图像，还用以上介绍的结合回避投影角度求导以及五点公式插值多项式对探测器坐标求导的Katsevich重建算法重建图像，并对比两种方法的重建图像质量.图2为Shepp-Logan头部模型重建图像z=0切片图，图3为Shepp-Logan头部模型x=0切片图.图2和图3中，（a）为投影数据没有添加噪声Katsevich重建图；（b）为投影数据没有添加噪声本文方法Katsevich重建图；（c）为投影数据添加高斯白噪声后Katsevich重建图；（d）为投影数据添加高斯白噪声后本文Katsevich重建图.

5.3 图像评价

在图像中，某一方向的灰度级变化率大，它的梯度也就大.因此可以用平均梯度值来衡量图像的清晰度，反映图像对细节对比的表达能力，还同时反映出图像中微小细节反差和纹理变换特征，所以本文用平均梯度来评价重建图像的清晰度.平均梯度越大，图像层次越多，清晰度越高.平均梯度定义如（17）式：

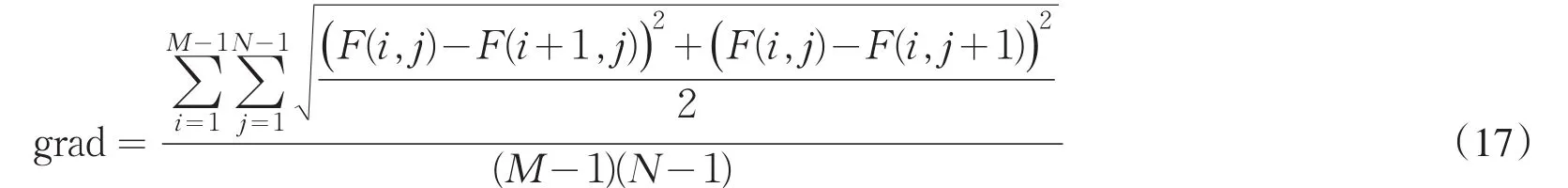
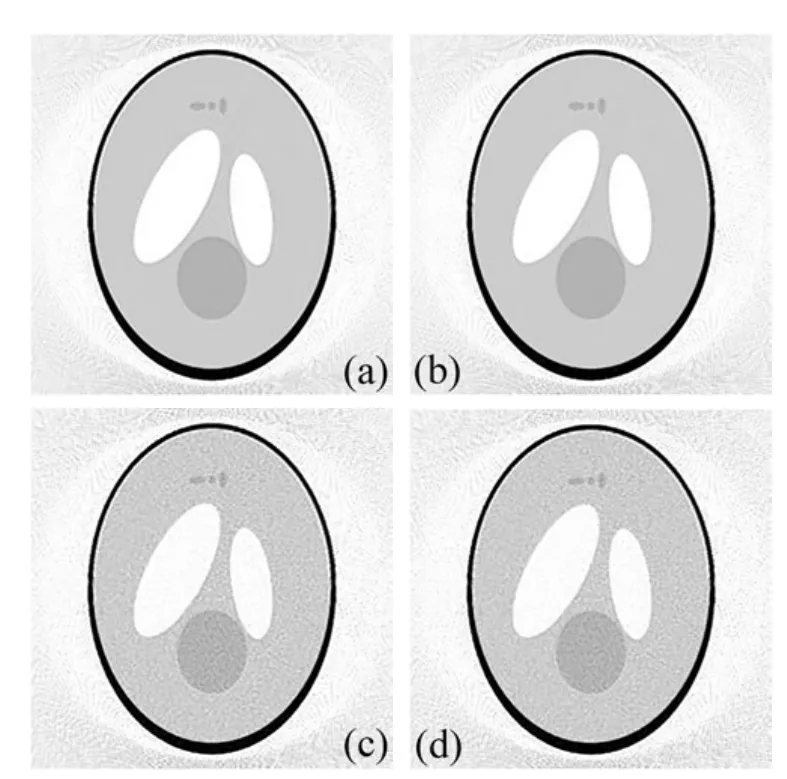
图2 Shepp-Logan头部模型重建图像z=0切面

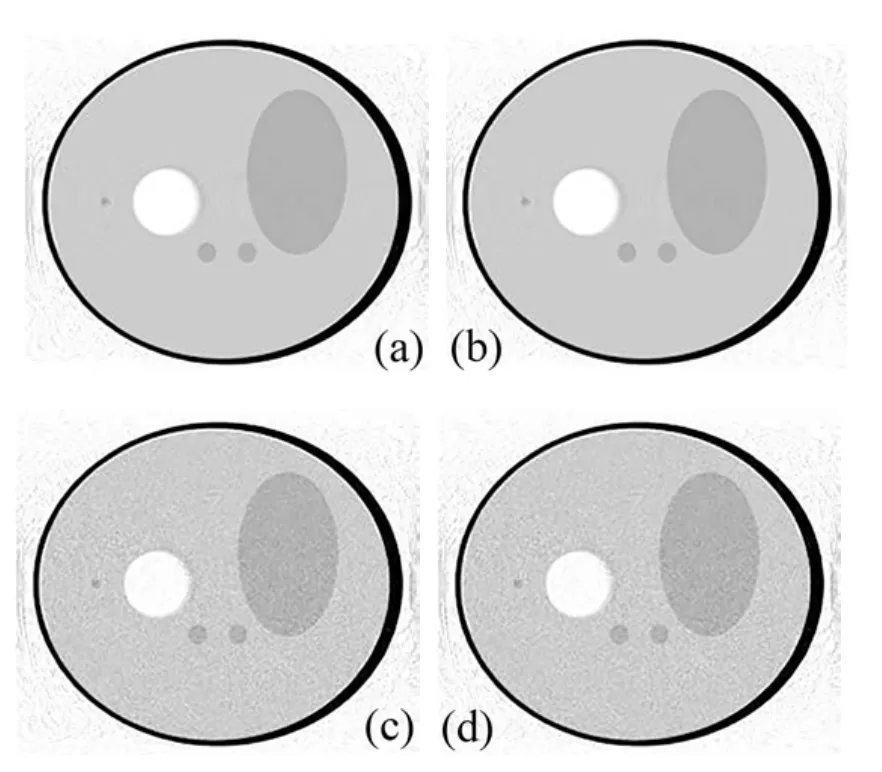
图3 Shepp-Logan头部模型重建图像x=0切面

式中：F(i,j)为图像的第i行、第j列的灰度值；M、N分别为图像的总行数和总列数.表1列出了分别用Katsevich直接求导法与本文Katsevich方法，对投影数据求导重建的切片的平均梯度值.

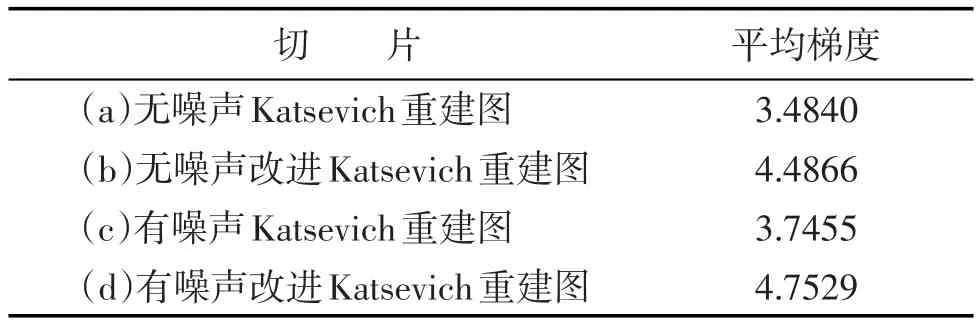
表1 图2、图3中各图像的平均梯度

由表1可以看出，用本文方法的重建切片比原始Katsevich的平均梯度值大，重建图像的清晰度更高.

6 结论

在实际CT成像系统中，获得投影数据混有各种噪声，然而Katsevich这种螺旋锥束精确重建算法对噪声敏感，所以有必要对这种算法进行改进，提高它的抗噪能力，所以应尽可能减少噪声对重建图像的影响.对噪声敏感的原因是投影数据求导会放大噪声的影响，并且需要进行高采样来达到更为精确的重建结果.本文结合了避开旋转角求导和对探测器横纵坐标五点方法求导方式.避开旋转角求导可以减少旋转角的采样，减少对病人的射线辐射.对探测器横纵坐标五点公式插值多项式求导方式，能够较好地处理边缘数据，从而使重建结果更加清晰，还能减少噪声对重建质量的影响.

[1]KATSEVICHA.Animprovedexactfilteredbackprojectionalgo⁃rithmforspiralcomputedtomography[J].AdvancesinApplied Mathematics,2004,32(4):681-697.

[2]YUHY,WANGG.StudiesonimplementationoftheKatsevichal⁃gorithmforspiralcone-beamCT[J].JournalofX-rayScienceand Technology,2004(12):97-116.

[3]KATSEVICHA.Ontwoversionsof3PIalgorithmforspiralCT[J]. PhysicsinMedicineandBiology,2004,49(11):2129-2143.

[4]YANGJS,GUOXH,KONGQ,etal.Parallelimplementationof Katsevich'sFBPalgorithm[J].InternationalJournalofBiomedical Imaging,2006:17463.doi:10.1155/IJBI/2006/17463.

[5]马建华,陈武凡.不含旋转角度微分的螺旋锥束CT重建[J].中国图象图形学报,2008,4(13):647-653.

[6]NOOF,PACKJ,HEUSCHERD.Exacthelicalreconstructionus⁃ingnativecone-beamgeometries[J].PhysicsinMedicineandBiolo⁃gy,2003,48(23):3787-3818.

[7]曾理,牛小明,邹晓兵.螺旋锥束CT重建Katsevich算法在含噪投影中的应用[J].计算机工程与应用,2007,43(26):187-189.

[8]王珏,陈教泽,谭辉,等.工业CT探测系统噪声特性研究[J].核电子学与探测技术,2010,7(30):929-934.

【编校：许洁】

ASpiralConeBeamCTKatsevichReconstructionAlgorithmforNoisedProjection

HUIMiao
(InstituteofInformationEngineering,SanmingUniversity,Sanming,Fujian365004,China)

Inpracticalengineeringapplications,theprojectiondatacontainsalotofnoise.TheKatsevichalgorithmisan exactimagingalgorithmwithgoodreconstructionimage.Thisalgorithmneedsderivationoperationonprojectiondatarota⁃tionangleandtwo-dimensionalcoordinatesofthedetector.Thederivationwillamplifythenoiseanddistorttherecon⁃structionimage.Combinedwiththeavoidderivationoftherotationangleandtheuseoffive-pointdifferentialmethodin⁃steadofdirectderivationtothedetectorcoordinate,thisalgorithmcanreducethesamplingrateofrotationangleandthe radiationtothepatientandX-raycost.Itcanlessentheerrorofthederivativeandthenegativeimpactcausedbythe noise.Thus,itimprovestheimagequality.

spiralconebeamCT;imagereconstruction;Katsevichalgorithm;projectiondataderivation

TP391.4

A

1671-5365(2015)12-0028-04

惠苗.一种含噪投影的螺旋锥束CTKatsevich重建算法[J].宜宾学院学报,2015,15(12):28-31. HUIM.ASpiralConeBeamCTKatsevichReconstructionAlgorithmforNoisedProjection[J].JournalofYibinUniversity, 2015,15(12):28-31.

2015-04-21修回：2015-06-29

资金项目：福建省教育厅科技项目(JA12302)

惠苗（1980-），女，讲师，研究方向为信息处理与重建、无损检测等

时间：2015-07-0110:15

http://www.cnki.net/kcms/detail/51.1630.Z.20150701.1015.002.html