互相关运算算法在微传感器检测中的应用
2015-01-17薛迎勃
薛迎勃,李 宏
(西安石油大学 电子工程学院,陕西 西安 710065)
当前,传感器正向微型化、智能化、数字化方向发展,研制小体积、轻重量、低功耗、快响应、宽频带、高精度、高可靠、智能化和环境适应能力强的新一代微传感器,成为这一领域的研究热点,其中的典型代表就是硅谐振式微传感器[1-3]。
因为硅谐振式微传感器采用微机械加工工艺,其敏感元件尺寸达到微米甚至亚微米量级,由此引起的 “微尺度效应”[4]使得其输出信号极其微弱,并存在严重的同频耦合干扰,导致其信噪比差,给信号提取带来相当大的困难。为克服这一缺陷,本文采用互相关算法进行检测[5],使用FPGA实现互相关运算,以达到从含有严重同频耦合干扰的微传感器的输出信号中提取有用信号的目的。
1 理论基础
电热激励硅微谐振式传感器的闭环控制系统如图1所示,其作用为找出电热激励微传感器的谐振点,并实现谐振状态的维持[6]。本文主要设计、实现该系统中的相关检测模块。
电热激励硅微谐振式传感器的输出信号由待测信号、频率为待测信号1/2的同频干扰信号和噪声组成,这里采用互相关算法对待测信号进行检测。
假设输入信号 X(t)中包含有用正弦信号 S2ω(t),同频耦合干扰正弦信号 Sω(t)以及噪声 N(t),即:


图1 传感器闭环控制系统框图Fig.1 Sensor is closed loop control system block diagram
输入信号与倍频参考信号Y2ω(t)的互相关函数为:
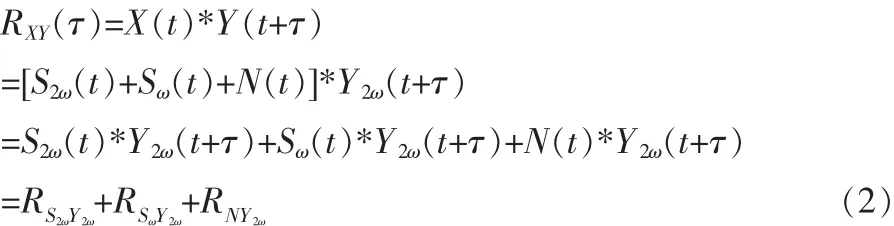
这里的参考信号实际上就是正弦信号S2ω(t)。当τ足够大时,考虑到 Y2ω(t)与 N(t)不相关,可得 RNY2ω=0,同时由于 Sω(t)和 S2ω(t)都 是 正 弦 信 号 但 频 率 不 同 ,可 得 RSωY2ω≈0, 所 以RXY(τ)≈RS2ωY2ω,可以将周期函数从噪声的淹没中提取出来。 编程实现时,周期函数的相关表示为:
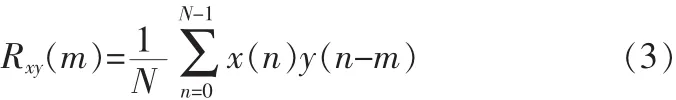
其中:m=0,1,2,…,M。 则,Rxy(1),…,Rxy(M)将组成一组与被采样周期信号x(n)同周期的正弦函数,再对这一系列自相关函数值的绝对值取均值,均值越大说明传感器输出信号幅度越大,最大均值max对应的频率点就是传感器的谐振频率点。
用Matalab软件对上述理论基础进行仿真分析。仿真时,时间从t=5e-6开始到t=12.8e-4结束,以5e-6为时间间隔,取 256个点为采样数据点;同时取参考信号 Y2ω(t)=cos(2π·ω·t),输入信号中所需的有用信号 S2ω(t)=cos(2π·ω·t),同频耦合干扰信号 Sω(t)=cos(π·ω·t)。 (其中 ω=14e3)
仿真结果如图2所示。

图2 互相关运算Fig.2 Cross-correlation arithmetic
(a)表示已知待测信号与参考信号进行相关计算的结果,(b)表示干扰信号与参考信号进行相关计算的结果,(c)表示包含干扰的传感器输出信号与参考信号进行相关计算的结果。(d)表示将它们放在同一张图上比较的结果。
由图2可以看出,只含有干扰信号时,相关计算结果非常小,而包含了干扰信号的传感器输出信号与参考信号相关计算的结果和待测信号与参考信号相关计算的结果非常接近。这说明,采用互相关运算对含有严重同频耦合干扰的微传感器输入信号进行检测,并从强噪声背景下提取有用信号,在理论上是可行的。
2 用FPGA实现
本模块所完成的功能是将传感器输出的含有很强的同频耦合和噪声干扰的输出信号与已知的参考信号进行互相关运算,并将有用的周期信号从噪声淹没中提取出来。
由于FPGA处理的都是数字信号,所以为使用FPGA实现相关运算这一工作,首先需要使用A/D采样将微传感器输出的模拟信号转换成数字信号输入FPGA,本文选用FPGA来控制A/D的运行,并通过FPGA控制A/D读取信号,实现对传感器输出信号的采样。然后,将转换得到的数字输入信号和参考信号存入FPGA相应地址的RAM中,直至获取到所需的N组采样数据为止,从而完成数据的采集工作。
在进行互相关运算过程中,首先应考虑如何运算,由公式
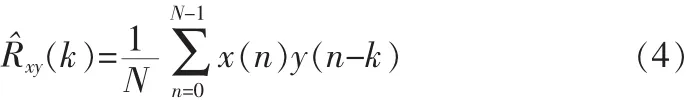
可知,数字信号进行的相关运算就是乘累加运算,即先乘再累加。其次考虑如何进行数据延时,也就是如何让传感器输出信号和参考信号中的两个N组数据进行移位。因为有用信号是实周期信号,为方便运算,每次只取一半数据进行乘累加,这样每次进行相关运算的数据个数是一样的,而且模块只需找到最大值,并且FPGA进行除法运算易产生误差,故不需要除N。 则公式(4)变形为公式(5):
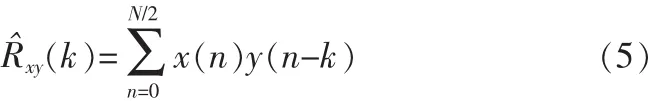
为了实现时延,需要在进行乘累加运算读取数据时进行移位,这里让读取数据时存储数据的RAM地址线发生变化就可实现这一功能。然后将乘累加运算的结果进行比较,这个值越大说明传感器输出的有用信号的幅值越大,最大值max对应的频率点就是传感器的谐振频率点,找出乘累加运算得到的最大值及其对应的时延τ。
本次设计,建立一个主任务和两个子任务(数据采集任务和计算任务)。主任务用于负责启动子任务,数据采集任务负责数据的采集和存储,计算任务负责互相关运算和结果的比较。总体算法流程图如图3所示。

图3 算法流程图Fig.3 Flow chart of algorithm
由图3可知,两路输入信号由计数器控制,通过A/D转换保存在相应的RAM中,存储设定的N组数据后,停止读数状态,进入计算状态。在计数状态下,对存储的这两组数据按照不同的时延进行互相关运算,比较查找出最大值和对应的延时,并将这个数据锁存,等待计算过程结束后,将结果输出。
3 结果分析
对频率为12.5 kHz的正弦波,以200 kHz的频率进行采样,得到16个12位数据如表1所列:
这两组数据理论上用公式5进行互相关运算且比较大小后结果为:时延τ=2,最大值为16 772 257。
用QuartusⅡ软件进行仿真,仿真结果如图4所示。
其中大矩形框内数据为输入的两组数据,小矩形框内数据为仿真结果。
仿真结果:时延 τ=2,最大值为 16 772 257,故仿真结果和理论值相同。下一步可将代码下载到FPGA开发板上再次调试。
将本系统应用于电热激励硅微谐振式传感器的控制系统,首先应进行开环测试,即只扫描而不锁定跟踪,然后再检测信号。本系统使用的电热激励微谐振式传感器(微悬臂梁)的谐振点激励频率是7 004 Hz,激励频率扫描范围是5~9 kHz。其频率特性曲线如图5所示,经过相关检测模块输出的结果能够运用于扫频过程。

图4 仿真结果Fig.4 The simulation results

图5 频率特性曲线Fig.5 frequency characteristic curve
根据上述分析,该模块能够实现相关检测功能,达到设计要求和性能指标。将该模块应用到电热激励微谐振式传感器的数字闭环控制系统中能正常工作。
4 结 论
本文首先对互相关检测的可行性进行了理论验证,其次完成了基于FPGA的互相关运算模块的设计。该模块使用Verilog语言编写代码,并经过QuartusⅡ软件仿真和FPGA开发板的硬件调试证明:该模块能够实现互相关检测功能,能从含有严重同频耦合干扰的微传感器输出信号中提取有用信号,且模块的采样频率和采样点数可以根据不同需求而设定,各项指标均达到设计要求,应用到电热激励微谐振式传感器的数字闭环控制系统中能正常工作。
[1]WANGZhe-yao,ZHOUYou-zheng,WNAG Chao-nan.A theoretical model for surface-stress piezoresistive microcantilever biosensors with discontinuous layers[J].Sensors and Actuators B 138 ,2009:598-606.
[2]Yang S M,Yin T I,Chang C.Development of a doublemicrocantilever for surface stress measurement in microsensors[J].Sensors and Actuators B121,2007:545-551.
[3]Seena V,Anukool Rajorya, Prita Pant, Soumyo Mukherji,V.Ramgopal Rao.Polymer microcantilever biochemical sensors with integrated polymer composites for electrical detection[J].Solid State Sciences 11,2009:1606-1611.
[4](荷)埃尔文斯波克.硅微机械传感器[M].北京:中国宇航出版社,2003.
[5]何孟珂,周浩敏,郝 欣.基于FPGA的硅谐振压力微传感器数字闭环系统设计[J].现代电子技术,2008(13):150-152.HE Meng-ke,ZHOU Hao-min,HAO Xin.Micro silicon resonant pressure sensor based on FPGA digital closed-loop system design[J].Modern Electronics Technique.13,2008:150-152.
[6]景占荣,羊彦.信号检测与估计[M].北京:化学工业出版社,2004.
