浅析图像模糊的基本频域恢复算法
2015-01-17郑中杰李展
郑中杰李展
(1.广东石油化工学院,广东 茂名 525000;2.暨南大学信息科学技术学院,广东 广州 510632)
浅析图像模糊的基本频域恢复算法
郑中杰1李展2
(1.广东石油化工学院,广东 茂名 525000;2.暨南大学信息科学技术学院,广东 广州 510632)
图像频域恢复是数字图像去模糊的一个重要的研究方向,在现实生活中有着广阔的应用前景和市场。本文针对常见的高斯模糊进行分析,使用频域上的逆滤波器、维纳滤波器和最小二乘恢复去除模糊,并对比它们的恢复效果。
图像恢复;高斯模糊;频域恢复
1 引言
近年来,随着电子数码产品特别是数码相机、数码摄像机、拍照手机的普及,以及计算机处理能力的提升,数字图像处理无论在军事、医疗、天文还是生活中都有着越来越重要的应用,而其中的图像模糊恢复的研究更成为其中的一个热点。
造成图像模糊的原因有很多,其中包括光学系统像差、大气扰动等,不同原因导致的模糊往往需要不同的处理方法。从技术方面来看,模糊是图像被卷积的结果,通常从频域上来去除图像模糊。
本文从频域上对图像的基本去模糊算法如逆滤波、维纳滤波及有约束最小二乘方法,通过编程实现来进行比较。
2 高斯模糊
图像的模糊有很多情况,其中高斯模糊常常被用于研究图像模糊。从数学的角度来看,图像高斯模糊的过程就是图像与正态分布做卷积。由于正态分布又叫做高斯分布,所以叫做高斯模糊。由于高斯函数的傅立叶变换是另外一个高斯函数,所以高斯模糊对于图像来说就是低通滤波器的效果。高斯模糊是一种图像模糊滤波器,它用正态分布计算图像中每个像素的变换。在二维空间定义为:

而高斯模糊定义为图像与高斯分布做卷积:

其中r是模糊半径,r2=x2+y2,σ是正态分布的标准偏差。
3 频域恢复
图像恢复处理的关键在于建立退化模型。输入图像f (x,y),经过某个退化系统后输出的是一幅退化的图像。为了讨论方便,把噪声引起的退出即噪声对图像的影响一般作为加性噪声考虑,这也与许多实际应用情况一致,如图像数字化时的量化噪声、随机噪声等就可以作为加性噪声,即使不是加性噪声而是乘性噪声,也可以用对数方式将其转化为相加形式。
原始图像f(x,y)经过一个退化算子或退化系统h(x,y)的作用,再和噪声n(x,y)进行叠加,形成退化后的图像g(x,y)。
图1为退化过程的输入和输出的关系,其中h(x,y)概括了退化系统的物理过程,就是所要寻找的退化数学模型。
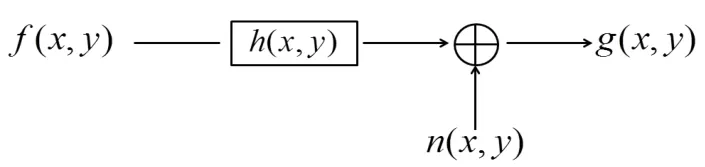
图1 图像的退化模型
根据退化图像g(x,y)和退化算子h(x,y)的形式,逆向地寻找原始图像f(x,y)的最佳近似估计。图像退化的过程可以用数学表达式写成如下的形式:

在频域上,上式可以写成:
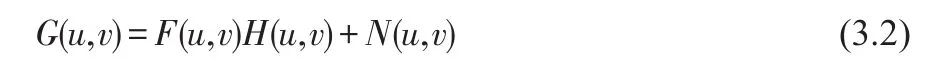
其中,G(u,v)、F(u,v)、N(u,v)分别是退化图像g(x,y)、源图像f(x,y)、噪声信号n(x,y)的傅里叶变换;H(u,v)是h(x,y)的傅里叶变换,称为光学系统在频域上的传递函数。
两式是连续函数的退化模型。可见,图像复原实际上就是已知g(x,y)求f(x,y)的问题或已知G(u,v)求F(u,v)的问题,它们的不同之处在于一个是在空域,一个是在频域。本文则只在频域上讨论。
3.1 逆滤波恢复
逆滤波是一种简单直接的无约束图像恢复方法。无约束恢复方法仅将图像看作一个数字矩阵,从数学角度进行处理而不考率恢复后图像应受到的物理约束。

在对n没有任何先验知识的情况下,图像恢复可描述为寻找一个原始图像f的估计ˆ,使ˆ在最小均方误差的意义下最接近退化图像g,即要使n的范数最小。


这里只需要将L(fˆ)对 fˆ求微分并将结果设为0,再设H-1存在,就可得到无约束恢复公式。

该式表明,用退化系统矩阵的逆来左乘退化图像就可以得到原始图像f的估计 fˆ。下面转到频率域中讨论。先不考虑噪声,根据式(3.2),如果用退化函数来除退化图像的傅里叶变换,便可以得到一个对原始图像的傅里叶变换的估计。

上式常称为逆滤波。如果把H(u,v)看作一个滤波函数,则它与F(u,v)的乘积是退化图像g(x,y)的傅里叶变换。这样用H(u,v)去除G(u,v))就是一个逆滤波过程。将式(3.1.5)的结果求反变换就得到恢复后的图像

实际中,噪声是不可避免的。考虑噪声后的逆滤波形式为

由式(3.1.7)可看出两个问题。首先因为N(u,v)是随机的,所以即便知道了退化函数,也不能精确地恢复原始图像。其次,如果H(u,v)在UV平面上取0或很小的值,N(u,v)/ H(u,v))就会使恢复结果与预期的结果有很大差距。实际中,一般H(u,v)随(u,v)与原点距离的增加而迅速减小,而噪声N (u,v)却变化缓慢。在这种情况下,恢复只能在距原点较近的范围内进行。换句话说,一般情况下逆滤波器并不正好是1/ H(u,v),而是u和v的某个函数,可记为M(u,v)。M(u,v)常称为恢复转移函数,这样图像退化和恢复模型可用图2表示。

图2 图像退化和恢复模型
一种常见的方法是取M(u,v)为如下函数:

其中w0的选取原则是将H(u,v)为0的点除去。这种方法的缺点是恢复结果的振铃效应较明显。一种改进的方法是取M(u,v)为:

其中k和d均为小于1的常数。d选的较小为好。
3.2 维纳滤波恢复
3.2.1 有约束恢复
与逆滤波这样的无约束恢复方法不同,有约束恢复的方法还考虑到恢复后的图像应该受到一定的物理约束,如在空间上比较平滑,其灰度值为正等。

与式(3.1.4)相似可得有约束恢复公式(令s=1/l)

3.2.2 维纳滤波器
维纳滤波器是一种最小均方误差滤波器。它可以从式(3.1.4)推出。
在频率域中,有约束恢复的一般公式可写成如下形式

其中Sf(u,v)和Sn(u,v)分别为原始图像和噪声的相关矩阵元素的傅里叶变换。
这里有几种情况:
① 如果s=1,大方括号中的项就是维纳滤波器;
② 如果s是变量,就称为参数维纳滤波器;
③ 当没有噪声时,Sn(u,v),维纳滤波器退化成理想逆滤波器。
当Sf(u,v)和Sn(u,v)未知时,式(3.2.3)可用下式来近似(其中K是一个预先设定的常数)

3.3 有约束最小平方恢复
维纳滤波的方法是一种统计方法。它用的最优准则基于图像和噪声各自的相关矩阵,所以由此得到的结果只是在平均意义上最优。有约束最小平方恢复方法只需有关噪声均值和方差的知识就可对每个给定图像得到最优结果。
有约束最小平方恢复方法也从式(3.2.2)出发,所以问题还是要确定变换矩阵Q。首先注意到式(3.1.4)实际是一个病态方程,所以有时解的振荡会很厉害。一种减小振荡的方法是建立基于平滑测度的最优准则,例如可最小化某些二阶微分的函数。f(x,y)在(x,y)处的二阶微分可用下式近似:

上式二阶微分可用f(x,y)与下面的算子卷积得到:

有一种基于这种二阶微分函数的最优准则是:
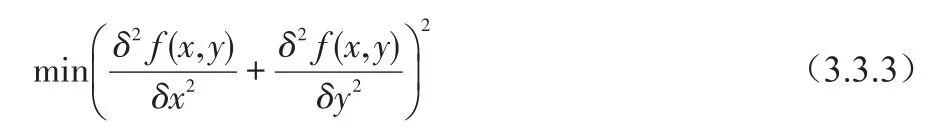
这里为避免重叠误差,可将p(x,y)扩展为:

若要求满足一下约束:

那么最优解可表示为:
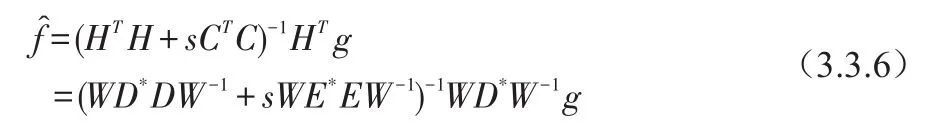
如将上式两边都左乘以W-1,得到:

可以导出下式:

上式与维纳滤波器有些相似,主要区别是这里除了对噪声均值和方差的估计外不需要对其他统计参数的知识。
式(3.3.8)表明需要调节s以满足约束式,所以只有当S满足这个条件时,式(3.3.8)才能达到最优。下面介绍一种估计s的方法。首先定义一个残差矢量r:
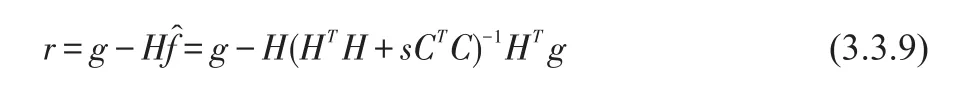
r是s的函数,这里希望调节s以满足:

这里a是一个准确度系数。如果‖‖r2=‖‖n2,则约束式()严格满足。一个简单的寻找满足式的s的方法是:
(1)赋给s某个初始值;
(2)计算 fˆ和‖‖r2;
(3)如果满足式(3.3.10),停止计算;否则就增加s(如果‖‖r2<‖‖n2-a)或减少s(如果‖‖r2>‖‖n2+a),然后返回(2),用新的s值根据式(3.3.8)获得Fˆ(u,v),在求其反傅里叶变换得到fˆ后继续计算。
为利用上面的过程进行有约束最小平方恢复需要确定‖‖r2和‖‖n2。首先,根据残差矢量r的定义式(3.3.9),利用傅里叶变换得到:

计算出R(u,v)后在求傅里叶反变换可得到r(x,y),由r(x,y)可计算‖‖r2:

下面考虑计算‖‖n2。先计算整幅图的噪声方差,它可用采样平均的方法来估计:

其中:

参照式(3.3.12),可知式(3.3.13)的双重求和就等于‖‖n2,所以有:

3.4 算法仿真效果及分析
对图像进行不同模板大小,标准差为10的高斯卷积,再加入高斯噪声。分别用逆滤波、维纳滤波和有约束最小二乘对降质图像进行恢复。由于篇幅限制,本文只展示维纳滤波和有约束最小二乘恢复滤波的部分处理效果(见图3),更详细的处理情况可以参照表1。

图3 几种图像频率恢复结果
从上面几幅图像可以看出最小平方恢复最能够有效地提高模糊图像的清晰度,而振铃效应也相对较小。
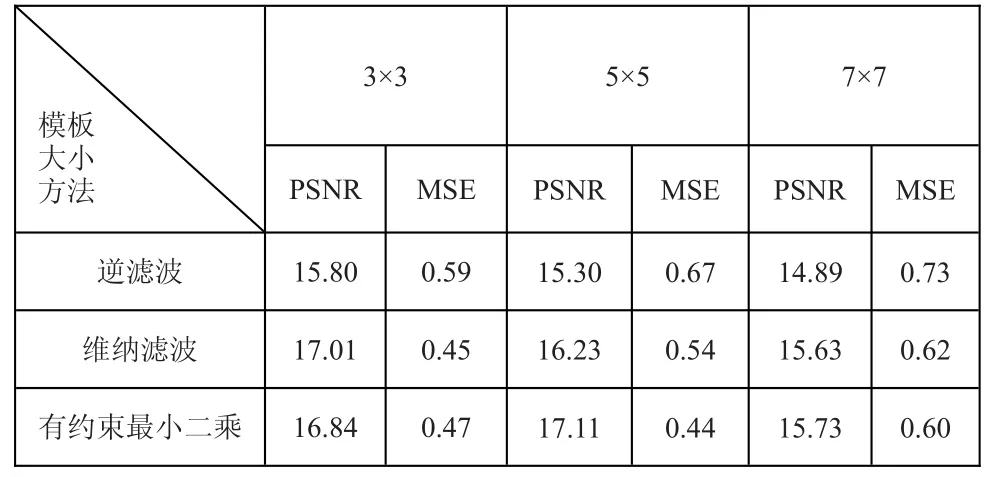
表1 几种滤波的性能比较
上述表明,三种频域恢复,当点扩散函数半径不太大的时候,有约束最小二乘方法对降质图像的恢复效果最明显。
4 总结
本文主要从高斯模糊对降质图像进行分析,包括对点扩散函数的研究,尤其是对高斯模糊的研究。针对影响图像质量的因素,分别对空域和频域的方法进行了解,从中引出频率恢复方法——逆滤波器、维纳滤波器和有约束最小二乘恢复。对于这三种频域恢复方法,都详细地分析了它们的原理,并进行恢复效果的比较。
[1]陈乃金,周鸣争,潘冬冬.一种新的维纳滤波图像去高斯噪声算法[J].计算机系统应用,2010,19(3).
[2]章毓晋.图形工程-图像处理[M].清华大学出版社,2006.
[3]K R Castleman.Digital Image Processing[M].Prentice Hall.Inc. 1998.
[4]J L Harris,Sr.Image Evaluation and Restoration[J].Opt.Soc.Amer. 1966.56:569-574.
[5]B L McGlamery.Restoration of Turbulence Degraded Images[J]. Opt.Soc.Amer.1967,57(3):293-297.
[6]C W Helstrom.Image Restoration by the Method of Least Squares [J].Opt.Soc.Amer.1967,57(3):297-303.
[7]D Slepian.Linear Least-Squares Filtering of Distorted Images[J]. Opt.Soc.Amer.1967,57(7):918-922.
[8]W K Pratt.Generalized Wiener Filter Computation Techniques[C]. IEEE Trans,Computers,1972:636-64.
Analysis of Basic Restoration to Deblured Images in Frequency Domain
Zheng Zhongjie1Li Zhan2
(1.Guangdong University of Petrochemical Technology,Maoming 525000,Guangdong; 2.Jinan University,Guangzhou 510632,Guangdong)
act】Image restoration in frequency-domain is an important research direction in image deblurring,which has widespread applications and marketing space in real life.This research focuses on analyzing common Gaussian blur.To eliminate it,inverse filtering,Wiener filtering and least square filtering in frequency domain are used.And last,comparison is made through experiments.
image restoration;Gaussian blur;frequency domain restoration
TP391.41
A
1008-6609(2015)03-0085-04
郑中杰,男,广东茂名人,硕士研究生,助教,研究方向:图像处理。
