基于组合预测模型的产业总产值的预测研究

李志鹏 李 薇 刘志杰,3

（1．贵州师范大学贵州省信息与计算科学重点实验室，贵州 贵阳 550001；2．贵州省发展和改革委员会，贵州 贵阳 550001；3．贵州师范大学网络与信息中心，贵州 贵阳 550001)

基于组合预测模型的产业总产值的预测研究

李志鹏1李 薇2刘志杰1,3

（1．贵州师范大学贵州省信息与计算科学重点实验室，贵州 贵阳 550001；2．贵州省发展和改革委员会，贵州 贵阳 550001；3．贵州师范大学网络与信息中心，贵州 贵阳 550001)

对于预测复杂的经济数据来说，选取合适的预测模型将是提高预测精度的关键。本文采用灰色模型与回归模型的组合预测模型对贵州省高技术产业总产值进行预测，利用了组合模型可以改善线性回归模型中没有考虑指数增长以及灰色模型中没有考虑线性因素的不足，从而达到提高预测精度的目的。并进行了计算机数值仿真实验表明了组合预测模型的有效性。

经济数据；预测；组合预测模型

1 引言

用数据挖掘的方法与模型对经济数据中有趣知识[1]的挖掘是一项非常复杂的工作，但它却可以为我们的政府、企业及有关行业把握未来的经济发展趋势、判断各个行业的发展前景并制定发展目标及发展战略等提供具有科学依据的指导。在二十世纪六十年代以来，世界经济的飞速发展致使了国内外大量的学者对经济预测进行了各方面的研究，提出了很多预测方法和模型[2]，有定量和定性预测方法、线性和非线性的预测模型，以期达到预测经济动态的目的。对于预测动态的影响因子较多的经济数据来说，其预测的质量和其所用的数据以及预测采用的方式是密不可分的。而经济数据具有很强的非线性性，各数据之间的相互影响关系没有明确的表达式，且呈动态波动的发展趋势。因此我们选择什么样的预测方法和模型来处理数据将是我们所要进行的预测的关键。本文所采用的线性组合预测模型[3,4]就是将不同的预测模型通过一定的方法进行组合，优化两种模型的不足[5]，以期达到取长补短的目的，从而提高预测结果的准确性。并对贵州省高技术产业发展统计数据集进行知识挖掘，最后对此模型做出分析和模拟评估。

2 组合预测模型的建立

2.1 灰色预测模型

若有一原始数据序列样本为x(0)={x(0)(1),x(0)(2)…x(0)(n)}，定义其累加生成序列公式为x(1)(k)=∑ki=1x(0)(i)（k=1,2…n），经过累加生成的序列为{x(0)(1),x(0)(1)+x(0)(2)…x(0)(1)＋x(0)(2)＋…x(0)(n)}，累加生成后的序列可以弱化原序列的随机性。经累加后的数据序列通过下述式（1）一阶微分方程的演化即可得到灰色预测模型[6]：

其中a称为发展灰数，u称为内生控制灰数。

可以将式（1）转化成为差分方程：

则有Y=Bb，根据微分方程的解的形式可以求得b=(BTB)-1BTY，将此值代入（1）式中得出灰色预测模型：

可求得还原值

其中k=0，1，2，…

2.2 线性回归模型

对于一元的线性回归模型其形式为y=β0+β1x+ε其中β0，β1是未知的真实回归系数，ε是误差项，多元回归模型是对一元回归模型的扩展，其形式为：

将

（2）式简化为Y=XB+ε，其中Y=y，X=[1，x1，x2，…xn]，B=[β0，β1，β2，…βn]T。

若考虑一个容量为m组的数据集X1，X2，…Xm，则令Xi= [1，x1i，x2i，…xni]，i=1，2…m。则有Y=[y1y2… ym]T，X为有m组数据的矩阵，B=[β0，β1，β2，…βn]T，ε=[ε1，ε2，…εm]T。ε是误差项，对其做出如下假设[7]：ε是一个期望为零的随机变量，ε的方差σ2是常数且与x1，x2，…xn的值无关，ε是一个正态随机变量且是相互独立的。根据上述误差项假设可以推导出目标变量y的分布：

1）E（y）=E（β0+β1x1+β2x2+…+βnxn+ε）=E（β0）+E（β1x1）+ E（β2x2）+…+E（βnxn）+E（ε）=β0+β1x1+β2x2+…+βnxn即对于任意的x1，x2，…xn取值，拟合值y的均值落在拟合回归线上。

2）对于任意的x1，x2，…xn取值，目标变量y的方差不变。

3）对于任意的x1，x2，…xn取值，目标变量y的值是相互独立的且是一个正态随机变量。

对于β0，β1，β2，…βn模型参数，其真实值可通过最小二乘法来估计。设目标变量的观察值为yi，经回归模型求得的拟合值为y'i=xiB'，令e=[ε1，ε2，…εm]T，残差为观察值与拟合值之差，记为ei=yi-y'i，则有e=Y-XB'，可以求得eTe=（Y-XB'）T（YXB'）=YTY-2B'TXTY+B'TXTXB'。根据最小二乘法要求得一个使得YTY-2B'TXTY+B'TXTXB'最小的一个B'，即求得一个使YTY-2B'TXTY+B'TXTXB'式中对B'求偏导为0时成立的一个B'的值，化简偏导方程可得参数为B'=（XTX）-1XTY。

2.3 组合预测模型

自上个世纪中叶，Schmitt第一次用组合预测的方法对人口数量进行了预测以来，世界各国的科学家、学者纷纷对各模型的组合进行了大量的研究，提出了许多有效的组合方法和新的组合模型。组合预测模型的原理就是将不同的预测模型采用某种特定的方式将他们结合起来，以达到取长补短的目的，从而提高预测结果的准确性的目的。本文所采用的灰色模型与线性回归模型的组合模型正是利用了这两个模型的组合可以改善线性回归模型以及灰色模型中所存在的不足并可以提高预测精度。

组合预测模型一般可以分为两种类型：线性组合和非线性组合。各界学者对于线性组合预测模型是研究很多，其应用也较广泛。建立线性组合预测模型的一个关键问题是对组合权重进行优化，且组合预测模型的精度仅与组合权重有关[8]，因此本文应该根据回归预测模型以及灰色预测模型各自的特点，对组合权重进行选取，以期达到充分结合两种模型的优势的目的。本文采用加权算术平均组合将灰色模型和回归模型两种预测模型的预测结果进行组合，从而得到新的组合预测模型。对两种模型的线性组合预测模型的描述如下：

设某预测问题的实际值序列为Y（tt=1，2，…n），灰色预测模型与回归预测模型的预测值分别为Y'1t、Y'（2tt=1，2，…n），加权系数记为ω1、ω2且满足条件ω1+ω2=1和ω1，ω2≥0，将组合预测值记为Y（'tt=1，2，…n），即要使得Y't对于预测值Y'1t、Y'2t越逼近越好。设加权算术平均组合预测模型的性能指标为：min Jt=∑2j=1ωj(Y't-Y'jt)2t=1，2，…n；令整理可得：Y't=ω1Y'1t+ω2Y'2tt=1，2，…n

模型中Y'1t、Y'2t都为预测之后的确定值，可以建立二次规划模型来确定ω1、ω2，其中要符合以下几条规则：min J't=∑2t=1(Yt-Y't)2、ω1+ω2=1、ω1，ω2≥0。

3 应用实例与分析

本文以贵州省高技术产业发展主要经济指标发展数据来检验通过上述步骤建立的组合预测模型，分别利用回归预测模型、灰色预测模型以及线性组合模型优化两个单项预测模型来进行预测。以2006-2010年的数据为基础来预测2011-2013年的贵州省高技术产业总产值。贵州省高技术产业主要经济指标数据表（部分）见表1。

表1 贵州省高技术产业主要经济指标数据表（部分） 单位：万元

3.1 灰色预测模型的实例建模

3.2 回归预测模型的实例建模

将表1中的数据化为亿元单位，利用上述的B'=（XTX）-1XTY公式求得多元回归预测模型的参数。得到预测模型为：y=-7.3791+0.1121x1+2.8659x2+1.2584x3

3.3 组合预测模型的实例建模

根据上述组合预测模型y=ω1y1+ω2y2以及权重系数的求解方法和约束条件求得权重系数ω1，ω2为（0.0637,0.9363）则可得到组合预测模型为y=0.5793 y1+0.4207y2

利用上述的三个模型进行数据预测，结果见下表2，本文采用相对误差百分比绝对值来作为评价指标。

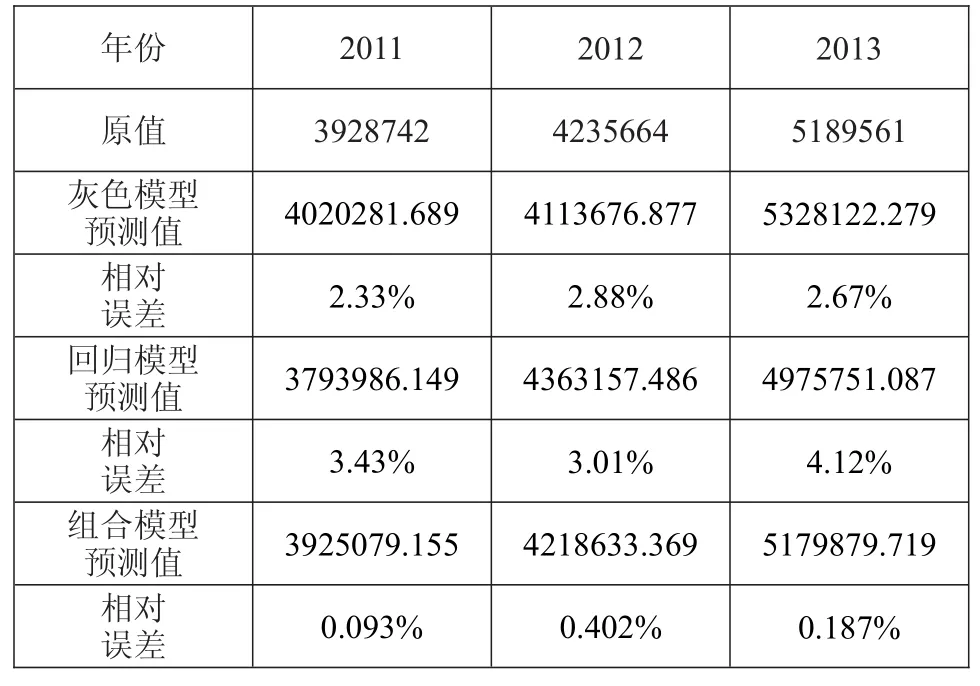
表2 预测结果比较 单位：万元

从表2中的结果可以看出本文提出的线性组合模型对于优化灰色模型与回归模型的单项预测方法起到了积极的作用，组合预测模型的预测结果较任一单项模型的预测结果在精度上有了明显改善。

4 结论

任一单项的预测模型在某个特定的预测数据集上都有其优势，也存在一定的局限性[9],灰色预测模型主要适用于单一的指数增长数序列，对其中出现的数据突变及异常的情况并不能作出很好的处理；回归模型是早期的发展的比较成熟的理论，它根据数据序列本身的连续性、相关性以及规律性等，在各影响因素相对平稳的情况下进行的预测，却考虑不到指数增长趋势，对长期的数据预测往往效果不理想。二者的组合模型综合了二个单项预测的优势，取长补短改善了改善线性回归模型中并不能顾及的指数增长以及灰色模型中没有线性因素的不足。本文采用灰色预测与回归预测的组合模型对贵州省高技术产业的总产值进行了预测，实例预测数据表明：二者的组合预测明显优于单独的预测模型的预测精度，在预测高技术产业发展总产值方面有实际的应用意义。

[1]Jiawei Han,Micheline Kamber．数据挖掘:概念与技术．范明,孟小峰译[M]．北京:机械工业出版社,2012．

[2]唐小我．预测理论及其应用[M]．成都:电子科技大学出版社,1992．

[3]Bates．J．M,Granger．C．W．J．The Combination of Forecasts．Operations Research Quarterly,1969, 20(4):451-468．

[4]甘健胜,陈国龙．线性组合预测模型及其应用[J]．计算机科学,2006, 33(9):191-194．

[5]Bann．D．W．Forecasting with More than one Model．Journal of Forecasting．1989,8(3):161-166．

[6]邓聚龙．灰色系统经济与社会[M]．北京:国防工业出版社,1985．

[7]Daniel T．Larose．数据挖掘方法与模型．刘燕权,胡塞全,冯新平等译[M]．北京:高等教育出版社,2011．

[8]马永开,唐小我．线性组合预测模型优化问题研究[J]．系统工程理论与实践,1998,18(9):110-114．

[9]许秀莉,罗键．一种新的组合灰色神经网络预测模型[J]．厦门大学学报,2002,41(2):164-167．

Industrial Output Prediction Research Based on Combination Forecasting Model

Li Zhipeng1Li Wei2Liu Zhijie1,3
(1.Key Laboratory of Information and Computing Science of Guizhou Province,Guizhou Normal University,Guiyang 550001,Guizhou; 2.Guizhou Province Development and Reform Commission,Guiyang 550001,Guizhou; 3.Network and Information Center of Guizhou Normal University,Guiyang 550001,Guizhou)

act】For predicting complex economic data,selecting suitable prediction model is the key to improve the prediction accuracy.This paper uses the combination of grey model and regression model to predict the high technology industry output in Guizhou. Taking the advantages of this combination model can improve the linear regression model by considering the exponential growth and improve the grey model by considering the linear factor,so as to achieve the goal of improving the prediction accuracy.And the computer numerical simulation results show the effectiveness of the combination forecasting model.

economic data;prediction;combination forecasting model

TP39

A

：1008-6609(2015)03-0062-03

李志鹏,男,湖南双峰人，硕士研究生，研究方向：计算机应用。

基于U-系列标准的电子政务应用解决方案，项目编号：2011BAH14B04。