基于CORDIC算法的雷达通信一体化波形产生技术研究

蒋德富，邵 健，钱 荣，徐玉超

（河海大学 计算机与信息学院，江苏 南京 211100）

随着技术的发展，作战平台面临的威胁日益增多，作战平台不得不配备越来越多的电子设备，设备的增多不但减弱了平台的机动能力，而且增大了雷达反射截面积，降低了其在现代电磁环境中的抗干扰能力和现代武器装备系统的整体作战效能。因此，必须把不同种类，不同用途的电子设备与当代先进的光电信息技术有机结合，使其具有探测、通信和对抗等多种功能[1]。

文献[2-3]提出了一种基于线性调频扩频技术的雷达通信一体化方式，这种方法是利用两个中心频率相同，调频斜率完全相反的线性调频信号分别表示雷达信号和通信信号，将两个信号相加形成具有雷达通信一体化的信号波形。这种方法存在一定的缺陷，首先它的雷达通信信号是近似正交的，这可能会在最后的分离上产生一定的误差，而且利用线性调频信号调制的通信信号得不到速度的保证，可能会无法正常传输通信信号。另外雷达通信信号相加之后不是恒定幅度的，这将导致一体化信号经过非线性放大器之后产生严重的交调失真，从而影响信号的探测能力和信息传输的能力。

本文基于LFM雷达信号波形和QPSK调制的通信波形调试。雷达和通信信号占据不同的频率。研究了雷达信号与通信信号的合成及调制技术，给出了仿真结果。

1 恒幅转换

为了兼顾放大倍数和放大效率，功率放大器需要工作在饱和区，这种非线性的工作模式会使合成信号产生严重的失真和交调，为了更好的传输信号，我们需要对信号做一定的处理。r1（t）和 r2（t）分别表示雷达信号和通信信号。 他们各自占据着不同的频率范围，由于雷达是脉冲信号，而通信信号是连续信号，它们的合成信号r（t）幅度是有起伏的，所以在进入功率放大器之前需要对信号进行恒幅转换，减少放大器对信号的非线性影响，通过放大器之后再将恒幅信号转化成为原始信号。

这里我们利用希莱克移相准则[6]将幅度变化的一体化信号 r（t）进行相位调制，调制的形式为:cos（w0t±cos-1r（t））。 （由于利用了逆三角函数，所以本算法只适用于r（t）幅度值小于1的情况，如果r（t）幅度值大于1，算法要有一定的变化，本文暂不做讨论）经过这样调制之后的波形是恒幅的，功放对这类信号的影响较小。调制时我们利用两路调制，调制形式分别为 cos（w0t±cos-1r（t））和 cos（w0t±cos-1r（t）），分别经过上变频和功率放大之后相加得到初始信号。

2 恒幅转化的CORDIC实现

2.1 CORDIC算法

CORDIC（Coordinate Rotation Digital Computer）即坐标旋转数字计算法的基本思想就是原始向量通过多次固定基准角度的旋转不断逼近目标向量[7]。

将图 1 的向量（x1，y1）旋转到向量（x2，y2）的方法如下式所示：

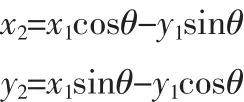
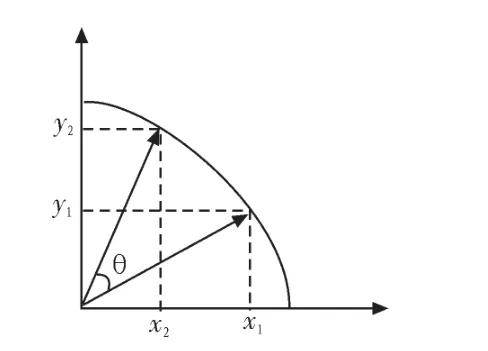
图1 向量示意图Fig.1 Map of vectors

把上面的式子变化一下得到：

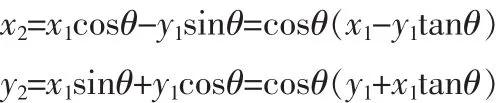
假设向量（x1，y1）旋转 n 次之后逼近向量（x2，y2），每次旋转的角度为Oi，则n次旋转的总角度为判决因子，它的值是+1或者-1，代表顺时针旋转还是逆时针旋转。与上同理，第i次旋转后的坐标关系为：

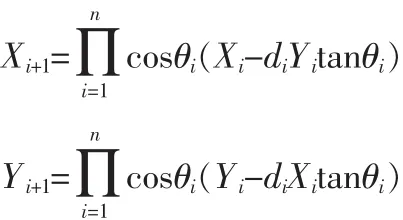
每次旋转角度的正切值：tanθi=2-i，则 θi=tan-1（2-i）。 引入旋转累加器Z，用于每次迭代过程中追踪累加的角度，Zi+1=Zidiθi，CORDIC 算法的迭代式如下：

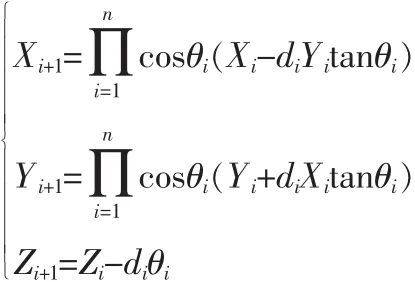
CORDIC工作模式分为旋转模式和向量模式两种，工作模式决定了控制因子 di，在旋转模式中，di=sign（zi）⇒zi→0，n次迭代之后我们得到：

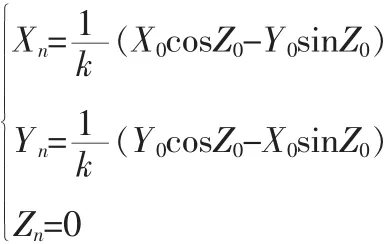
向量模式中，di=-sign（xiyi）⇒yi→0，n 次迭代后我们得到：

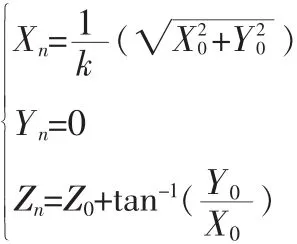
这是在圆坐标系下的结果，另外在线性坐标系和双曲线坐标系下迭代的结果是不同的，总结成下表：

表1 CORDIC工作模式Tab.1 working mode of the CORDIC

2.2 利用CORDIC的算法实现

上面提到恒幅转换的调制方式是 cos（w0t±cos-1r（t）），为了CORDIC算法更简单的实现，我们将这个公式做一定的变根据上面的结果，我们可以利用两个CORDIC模块实现恒幅转换，结构图如图2所示。

CORDIC算法中指只含有移位运算和加减运算，所以特别适合用FPGA来实现。FPGA的工作频率高，有利于雷达信号等高频率信号的处理。

3 恒幅转换算法仿真结果

我们选择的雷达信号是中心频率10 M，带宽10 M的线性调频信号，如图3所示。通信信号是带宽为10 M，中心频率为30 M的QPSK信号，如图4所示。

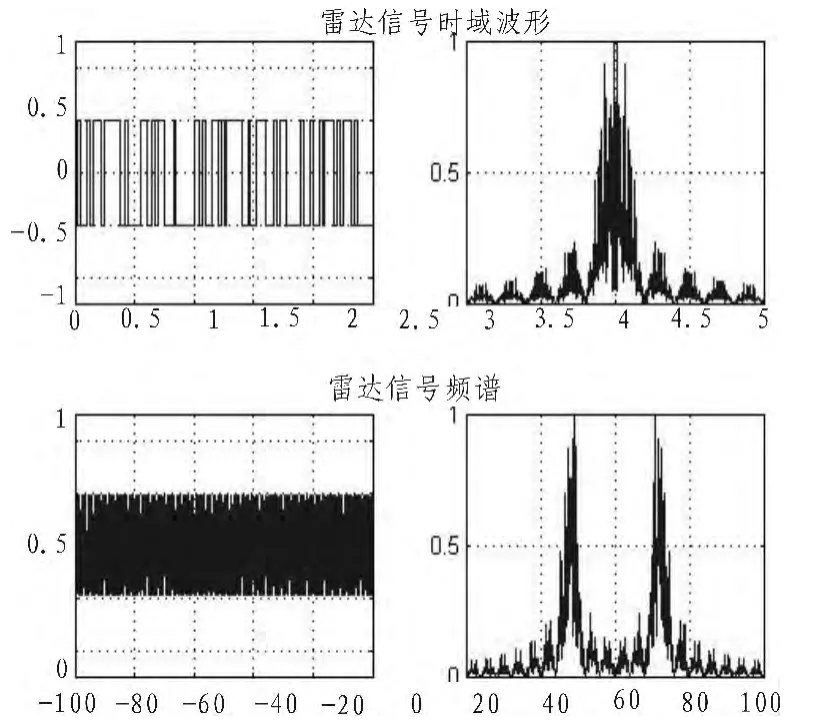
图3 雷达信号图Fig.3 Radar signal

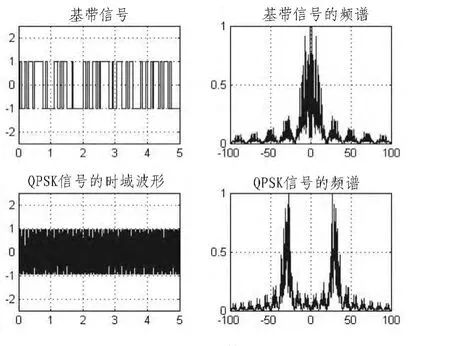
图4 QPSK信号Fig.4 QPSK signal

由于这个算法是建立在幅度值小于1的基础上的，我们在把两个信号相加之前各乘以了一个系数0.5，这样才能保证相加信号的幅度也小于1，，图5给出了相加之后一体化信号的波形图。

此时我们可以观察到在频域中雷达信号和通信信号是分离的，但是时域中合成信号的幅度是不断变化的，如果直接将它进行功放，将产生严重的交调和失真，所以在功放之前我们应用上述相位调制进行了恒幅转换，得到图6的恒幅波形。

调制后的信号波形幅度恒定，大大减小了功率放大器的非线性影响。将两路分别调制的信号上变频和功率放大之后相加得到图7所示的波形。这就是初始的一体化信号经过上变频和功率放大之后的波形。

4 结束语

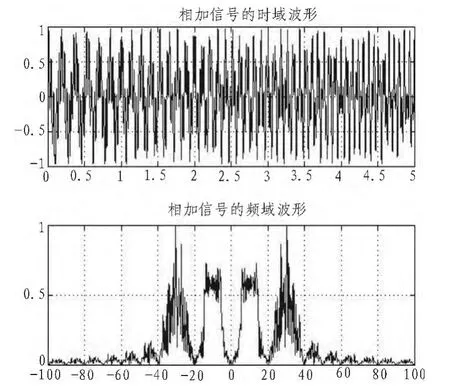
图5 恒幅转换后的时域波形Fig.5 Waveform in time domain after conversion

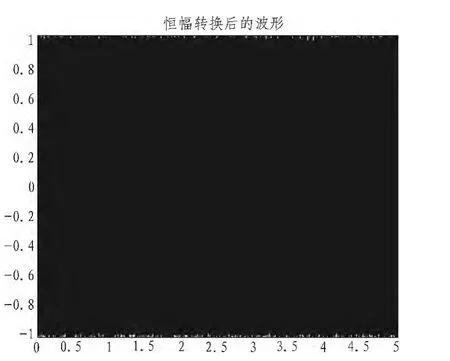
图6 相加之后波形特性图Fig.6 Properties of waveform after adding

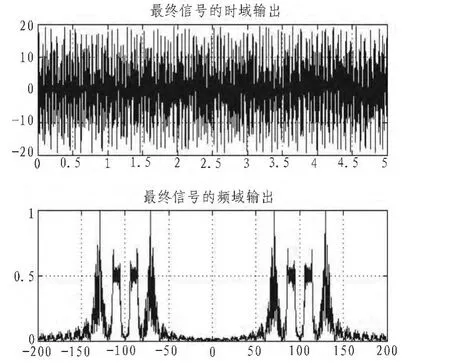
图7 最终输出波形特性Fig.7 Properties of the final output waveform

本文重点研究如何减少功率放大器对于一体化信号的影响，提出了基于cordic算法的恒幅转换，通过最后的仿真图可以看出在一体化信号进入功放之前，这个方法有效的把信号转换成了恒定幅度的信号，然后在经过功放之后又把信号还原成原来的初始信号，从仿真图也可以看出信号并没有失真。

[1]张明友.雷达一电子战一通信一体化概论[M].北京：国防工业出版社，2010.

[2]Roberton M，Brown E R.Integrated radar and communications based on chirped spread-spectrum techniques[C]//Microwave Symposium Digest，2003 IEEE MTT-S International.IEEE，2003，1:611-614.

[3]李晓柏，杨瑞娟，程伟.基于 Chirp信号的雷达通信一体化研究[J].雷达科学与技术，2012，10（2）:180-186.LI Xiao-bo，YANG Rui-juan，CHEN Wei.Integrated radar and communication based on chirp[J].Radar Science and Technology，2012，10（2）:180-186.

[4]Antonik P，Bonneau R，Brown R，et al.Bistatic radar denial/embedded communications via waveform diversity[C]//Radar Conference，2001.Proceedings of the 2001 IEEE.IEEE，2001:41-45.

[5]Jeong Y K，Song T K.Simultaneous multizone focusing method with orthogonal chirp signals[C]//Ultrasonics Symposium，2001 IEEE.IEEE，2001，（2）:1517-1520.

[6]Chireix H.High power outphasingmodulation[J].Radio Engineers，ProceedingsoftheInstituteof，1935，23（11）:1370-1392.

[7]王晶洋，林婧，王宏，等.基于 CORDIC算法的三角函数实现[J].数字技术与应用，2011（8）:3-4.WANG Jing-yang，LIN Jing，WANG Hong，et al.Trigonometric realization based on CORDIC algorithm[J].Digital Technology Applieation，2011（8）：3-4.