Dijkstra算法在露天矿运输中的应用
2015-01-16武文越宿海芬
武文越 宿海芬
(内蒙古包钢钢联股份有限公司巴润矿业分公司)
Dijkstra算法在露天矿运输中的应用
武文越 宿海芬
(内蒙古包钢钢联股份有限公司巴润矿业分公司)
由于露天矿路况复杂,汽车运输中油耗、轮胎消耗、汽车磨损严重,且随着采场推进、运距增大,运费大幅提升。选择最短的运输路径,降低运输成本是当务之急。采用Dijkstra算法,能够快速找出最短运输路径,有效降低运输成本。
露天矿 汽车运输 Dijkstra算法 最短路径
内蒙古某露天铁矿采用φ310 mm机钻穿深孔,高精度雷管和组合雷管2种爆破网络连接方式,高精度雷管逐孔起爆爆破矿岩。矿岩破碎效果较好,为节约成本,该矿也采用普通雷管排间起爆方式爆破。在岩性允许的条件下,普通雷管爆破后矿岩块度,能够满足小型挖机作业要求。爆破后采用6~8 m3,16 m3大型电铲装车,220、108 t级电动轮矿用自卸汽车运矿。由于电动轮矿用自卸汽车回转半径及设备体积和吨位的限制,只能将矿石从采场拉运至采场南矿石台,再由双桥卡车将矿石运至破碎站。
该出矿点位于采场西1536段,开采条件复杂,不利于大型设备作业,采用双桥卡车运输,可有多条路径选择。40 t双桥卡车相对于该矿自有电动轮汽车,具有曲线半径小、运输坡度大、不受地形限制等优点,可减少运输线路长度,降低运输成本。
汽车运输合理开采深度为100~150 m,合理运距为3 km。该露天矿现采深为162 m,露天矿进入深部开采后,汽车运输成本逐渐增加。运距增加后,运输燃料、轮胎消耗巨大,制约了汽车运输的运用。为此,在目前汽车运输条件下,采用Dijkstra建立数学模型,计算选择最短运输路径,以有效节约运输成本。
1 数学模型建立及求解
1.1 Dijkstra算法
Dijkstra算法也称为双标号法,是由狄克特斯拉(Dijkstra,1959)提出的,是目前多数系统解决最短运输路径问题通常采用的理论[1]。Dijkstra算法主要特点是以起始点为中心向外层层扩展,直到终点为止。该算法在工程中容易实现,故而引起相关领域内学者的关注[2-3]。
双标号法,即对图中的点Vi赋予标号P(Vi,λi),标号P(Vi)表示从起点Vs到Vi的最短路径的长度,标号λi表示在Vs到Vi的最短路径上Vi前面一个邻点的下标,即用于标识路径,从而可对终点到始点进行反向追踪,找到Vs到Vi的最短路径。Dijkstra算法适用于每条弧权数非负的情况。
1.2 基本步骤
(1)步骤一,给起点vs标号(0,s),表示从v1到v1的距离为0,vs为起点。

(3)步骤三,如果上述弧的集合A=φ,表示从所有已赋予标号的顶点出发,不再有这样的弧,则计算停止。对于已经标号的顶点,可以求出从vi到达这个顶点的最短路径,对于没有标号的顶点,则没有从vi到达这个顶点的路径。如果弧集A≠φ,转向步骤4。
(4)步骤四,对弧集A中的每条弧(vi,vj),计算Tij=P(Vi)+ωij,在所有的Tij中,找到值为最小的弧,假设为(vs,vt)。需要特别注意的是,如果上述Tij值为最小的弧有多条,并且这些弧第二个顶点vj相同,表示存在多条最优路径,此时任意选择一条路径,最终最优路径不变,vj应得到多个双标号。
(5)步骤五,给弧(vs,vt)的终点vt赋予双标号(P(Vt),s),返回步骤2。经过上述循环计算,将会求出v1到一个顶点vj最短路径及长度,进而得到一个顶点vj及双标号。如果图中共有n个顶点,最多计算(n-1)个循环,即能得到最后最短路径的结果。
1.3 模型建立
从工作面到卸矿点的路径很多,线路系统较复杂时,人工方法找出最短路径较为困难,用网络的方法,对运输线路系统进行抽象简化,用线代替每条线路,固定路口、零时斜坡路口即是节点,将节点标号[4]。
任意两点A、B直线距离:
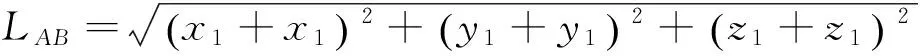
(1)
任意两点A、B弯道距离:
(2)
将相关点三维坐标输入Excel,调入函数,可得到各路线长度。
1.4 Dijkstra算法求解
给起点v1标号(0,1),表示从v1到v2的距离P(v1)=0,v1为起点,图1为模型建立及求解过程图。

图1 模型建立及求解过程

T13=P(v1)+ω13=0+0.5=0.5;T15=P(v1)+ω15=0+1=1;T16=P(v1)+ω16=0+1.3
=1.3;T17=P(v1)+ω17=0+1.2=1.2.
=T13=0.5.
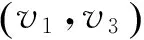
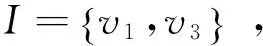

T15=P(v1)+ω15=0+1=1;T16=P(v1)+ω16=0+1.3=1.3;T17=P(v1)+ω17=0+1.2=1.2;T32=P(v3)+ω32=0.5+0.15=0.65;T35=P(v3)+ω35=0.5+0.9=1.4.

重复上述步骤,直至终点。反向追踪,求出v1→v5→v8→v9路径为最短运输距离,运距为3.4 km。
2 结 论
采场道路条件复杂,既有固定运输线路,也有临时斜坡路,选择最短运输路径对降低汽车运输成本有重要意义。Dijkstra算法可以快速确定多运输路径条件下的最短运距问题,可以有效节约露天矿汽车运输成本。
[1] 张福浩,刘纪平.一种基于Dijkstra的海量空间数据最短路径算法[J].辽宁工程技术大学学报,2009,28(4):554-555.
[2] 李大东,孙秀霞,彭建亮,等.基于可视图的改进Dijkstra 算法[J].电光与控制,2010,17(3):40-41.
[3] 章永龙.Dijkstra最短路径算法优化[J].南昌工程学院学报,2006,25(3):31-32.
[4] 巩艳芬,刘 吟,于惠贤,等.Dijkstra 算法在企业物流运输网络中的应用[J].大庆石油学院学报, 2005, 29 (4): 104-105.
Application of Dijkstra Algorithm in Open-pit Mine Transportation
Wu Wenyue Su Haifen
(Barun Mining Co.,Ltd., Baotou Steel (Group) )
Because of the complex road conditions in open-pit mine,the oil consumption,tire consumption and automobile abrasion are serious,and the automobile transportation's cost is increased with the increasing of distance in open-pit mine.So,it is necessary to choose the shortest transportation path and reduce the cost.The Dijkstra algorithm is adopted so as to identify the transportation shortest path and reduce the cost effectively.
Open-pit mine, Automobile transportation, Dijkstra algorithm, Shortest path
2015-06-10)
武文越(1984—),男,助理工程师,硕士,014080 内蒙古包头市。
