压缩感知在磁共振成像中的应用研究

钟晓燕，卜祥磊，田辉勇

(1南方医科大学生物医学工程学院，广州510515;2广州市妇女儿童医疗中心 设备科，广州510263)

压缩感知在磁共振成像中的应用研究

钟晓燕1，卜祥磊2，田辉勇1

(1南方医科大学生物医学工程学院，广州510515;2广州市妇女儿童医疗中心 设备科，广州510263)

压缩感知是建立在矩阵分析、概率统计理论及泛函分析等基础上的一种新颖的信号获取方式，它可以以低于传统Nyquist采样定理所需的采样数据准确重建原始信号。本文在压缩感知基本理论的基础之上论述了其与磁共振成像相结合的基本原理，包括磁共振图像的稀疏表示、K空间采样轨迹的设计、优质重建算法的选择，并简要介绍了压缩感知在磁共振成像中其他方面的一些应用。

压缩感知;磁共振成像;稀疏表示;图像重建

0 引言

磁共振成像(Magnetic Resonance Imaging，MRI)是一种利用生物原子核自旋特性，通过激励静磁场中的物体产生磁共振信号，然后对其进行空间信息编码，最后由傅立叶变换获得图像数据的技术。由于该技术具有无辐射、不需要使用造影剂、较高的人体组织分辨率以及可任意方向断层等特点，已经成为一项重要的医学辅助诊断技术。然而，磁共振成像仍然存在成像时间较长的不足。因此，缩短数据采集时间仍然是磁共振成像发展的核心目标之一。

目前，从硬件性能提升的角度来讲，成像速度的加快基本上已经达到了极限。因此，研究人员开始更多地关注磁共振成像的重建算法，通过研究更快速的K空间采集方案来达到减少磁共振扫描时间的目的。缩短扫描时间的途径主要有以下三种:一是高速扫描序列的设计，该方法通过设计高速扫描序列，实现在一次激发内获得整幅图像的信息。然而这种技术受硬件条件的制约，已经接近达到可以改善的极限。二是并行成像技术，该方法采用相控阵线圈同时接受感应信号，并通过相控阵线圈对空间灵敏度的差异来编码空间信息，减少了相位方向梯度编码的次数，从而实现大幅度缩短扫描时间，提高成像速度。三是部分K空间采样方法，该方法利用K空间数据的共轭对称性，只采集部分K空间数据，以达到缩短扫描时间的目的。

由Donoho［1］与Candes［2］等人2006年提出的压缩感知技术(Compressed Sensing，CS)是近年来新兴的一个研究方向。该理论表明，当信号具有稀疏性或者可压缩时，设计随机测量矩阵在K空间稀疏采样，通过稀疏重建算法就可以获得高质量的重建图像。

1 基于压缩感知的磁共振成像原理

1.1 基本理论

对于磁共振成像而言，首先，大部分磁共振图像都具有稀疏性;其次，磁共振MRI采样的原始数据K空间为图像的傅里叶数据。因此利用压缩感知理论能够极大地减小傅里叶变换域的采样数据，从而降低扫描时间。

1.2 数学模型

CS理论的数学模型描述如下:假设x为一维的空间向量，向量长度是N，它可以用一组正交基线性表示为:

式中φψ为M×N的矩阵。可见，式(3)的逆向求解是一个NP－HARD问题，但是Candes等指出，如果Θ满足约束等距性条件，同时，，则原始K稀疏信号x可通过求解某种最优化问题由测量值重构。即:

将CS应用到磁共振重建中:在压缩感知理论中将信号从高维到低维随机投影的过程，对应到MRI中即为获取K空间样本的过程。因此与式(4)相对应，α相当于磁共振图像x在某个域中的稀疏表示，而φ则是欠采样的傅里叶变换操作FU，FU由采样方式决定，M＜N则意味着获得的K空间采样数据是不完全的，即欠采样，通过式(4)知，MR图像可以通过求解一个有约束的优化问题重建出来。

1.3 关键要素

当前CS理论主要涉及三个核心问题:信号的稀疏表示;非相干性或等距约束性准则的测量矩阵设计;优质重建算法的选择。将压缩感知理论应用到MRI重建同样需要解决相应的这三个问题。

（1）处理的原则：技术上可行，经济上合理，确保工程质量。因为在建筑结构设计和施工中最难以驾驭的并不是上部结构，而是该工程的地基和基础问题，尤其是在地基处理上，不同地域的差异很大，如果处理不当，一旦发生事故，难以补救，甚至造成灾难性的后果。

(1)MR图像的稀疏表示:常用稀疏变换有傅立叶变换、小波变换、Curvelet基、Gabor基、差分变换及冗余字典等。磁共振图像中较为常用的稀疏变换有小波变换和全变差分变换。例如，Lustig等［3］着眼于利用TV处罚项和小波变换来构造基于压缩感知的磁共振图像重建模型。图1以磁共振脑部图像为例给出了原图及其在不同稀疏域内的表达。

研究表明，由于二维小波不能对二维信号中的边缘和纹理提供最优表示。因此，用于高维信号处理的多尺度几何分析方法应运而生，比较有代表性的包括曲线波(Curvelet)、轮廓波(Contourlet)、脊波(Ridgelet)、以及剪切波(Shearlet)等。例如:文献［4］提出了一种将轮廓波变换作为图像稀疏变换的方法，实验结果表明轮廓波变换在图像去噪和压缩感知稀疏化信号方面具有明显优势。国内学者屈小波等通过将曲波、方向性小波等变换引入MRI重建的过程中，得到了较好的重建效果。

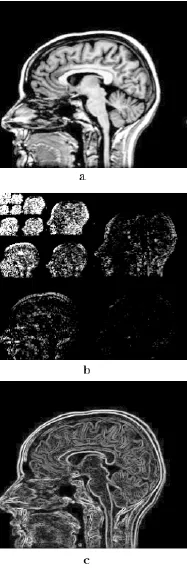
图1 MR图像在不同稀疏域内的表示

目前，用字典学习的方法来构建稀疏变换字典是一种热门的方法，它的核心思想是构造一个超完备的字典，信号可以用字典中少数几个原子的线性组合来表示，这样就可以使信号达到最佳的稀疏效果。例如，2007年Peyer等［5］将正交基范围拓宽到了正交基字典，该字典由多个正交基组合而成，可根据信号的不同选择最合适的正交基，以实现对信号的最优表示。Aharon等［6］提出以K均值聚类方法为基础的 K－SVD(single value decomposition)算法可用来设计字典集，使正交基自适应性地依据信号更新，进而获得信号在字典集上更好的稀疏表达形式，并且应用于磁共振图像重建。

(2)K空间采样轨迹设计:由压缩感知理论可知，要精确的重构图像，测量矩阵与稀疏矩阵之间必须满足受限等距特性－RIP(Restricted Isometry Property)性质，所谓受限等距特性指的是:对于一个具有K项稀疏的矢量x，测量矩阵与稀疏矩阵构成的观测矩阵Θ必须满足如下条件:

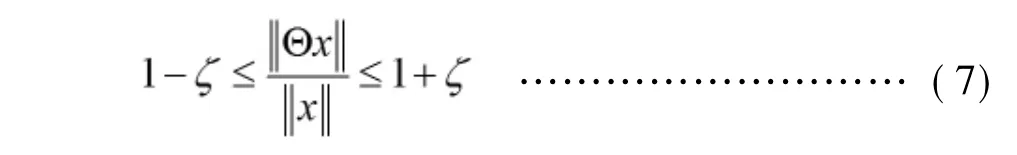
其中，ξ＞0。在CS理论中，常把测量矩阵和稀疏矩阵合在一起(Θ=φ×ψ)称为观测矩阵，由于直接判断观测矩阵是否满足受限等距特性比较困难，相关学者提出可用非相关性来判断观测矩阵是否符合RIP准则:即如果测量矩阵φ和稀疏变换基ψ是不相关(Incoherent)的，则Θ=φ×ψ很大概率上是满足RIP准则的。相关性定义如下:

对于磁共振成像而言，压缩感知中测量矩阵的设计就相当于是傅里叶采样方式的设计。

目前为止，最常用的采样系统是图2(a)笛卡尔采样，其采样所得到的数据相关性远远高于随机采样所得到的数据，重建图像质量不高，有较多伪影。研究表明，满足高斯分布轨迹的采样矩阵与任何稀疏基之间的相关性都非常低，并且也满足相应的RIP性质。而射线状采样矩阵与螺旋线采样矩阵其采样轨迹大部分都满足高斯分布，因此与笛卡尔采样相比，射线状采样轨迹图2(b)对具有高对比度的物体采样后图像重构的质量更高。螺旋采样轨迹图2(c)在梯度系统硬件中的使用其效率非常高，特别是在实时成像和快速成像中的应用，但这种采样轨迹采样得到的数据进行重构时，其重构算法复杂，需要利用网格重建算法来重建图像。随机点采样矩阵虽然能完成采样过程，并且也能重构图像，但是现实中会受到硬件以及生理条件的限制。

图2 常用k－space采样轨迹

(3)重建算法:重构的过程，实际就是由少量观测y恢复原始稀疏信号x的过程。根据前面的讨论可知，只要Θ是满足等距离约束条件的随机观测，公式(3)的欠定方程就有解。信号x的恢复可通过逆向求解稀疏表示α来完成，即α=ψTx。由此压缩感知的信号重构问题被转换为约束条件下最优化问题的求解过程，如下式所示。

实际问题中0范数最小化的求解是NP－hard问题，因此寻找其等效快速算法成为非常重要的课题。研究中，Chen和Donoho等人指出，1范数最小化问题求解近乎全概率和0范数最小化求得相同解，使得0范数问题可以转化为凸优化问题求解，如公式(10)所示。

对应到磁共振成像中，则x相当于待恢复图像，y代表观测到的k－space数据，ψ为稀疏基，φ为部分傅里叶变换Fu，重建问题转化为求解一个受限的优化问题:

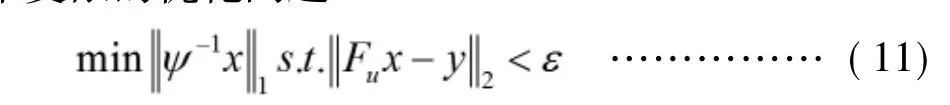
式中ε控制重建结果和观测值之间的一致性。有时在进行稀疏变换时，既采用其它稀疏变换，也会包含有限差分，可以理解为要求图像在某指定变换形式下和有限差分下均稀疏。此时等式就会变形为以下形式，

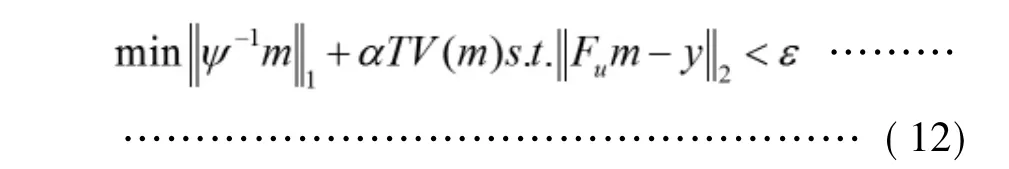
其中α调节ψ稀疏和TV稀疏两者的比重。

具体的重建算法大致可分为三类:

①贪婪算法。主要有匹配追踪算法(Matching Pursuit，MP)、正交匹配追踪(Orthogonal Matching Pursuit，OMP)、正则化 OMP算法(Regularized OMP，ROMP)及分段OMP算法(Stagewise OMP，StOMP)等。

②凸优化算法。主要包括基追踪算法(Basis Pursuit，BP)、内点法(Interior－Point Method)和梯度投影法。基追踪算法在每次迭代时从过完备原子库(即测量矩阵)中寻找最佳的匹配原子。

③组合算法。主要包括傅里叶采样，链式追踪(Chaining Pursuit，CP)和 HHS(Heavy Hitters on Steroids Pursuit)追踪等等。这类方法适用于针对大规模数据的问题，通过对信号进行结构化抽样，要求信号的采样可以支持快速分组测试快速重建。

2 压缩感知在其他磁共振成像方法中的应用

2.1 并行成像

目前比较流行的并行成像算法主要有三类:基于图像空间的技术(SENSE)、基于K空间的技术(GRAPPA、SMASH)还有基于图像空间和K空间的混合的技术(SPACE－RIP)。Ye等［7］提出了一种快速数值方法—部分并行MRI图像重建的加速技术，通过变量分裂和获取最优步长的方式来减少计算量和加快收敛。还有一些研究工作也尝试将并行成像技术和压缩感知技术相结合，以进一步提高成像速度［8，9］。

2.2 动态成像

动态磁共振成像是一种控制动态过程的技术。最先将压缩感知思想应用到动态磁共振成像的是Lustig等人。他提出的k－t SPARSE方法，成功的将压缩感知理论应用到心脏成像。HongJung等［10］提出的k－t FOCUSS算法并将之用于动态MR图像的重建，Chenlu Qiu等［11］提出了KF－CS算法将卡尔曼滤波器引入到动态MR图像的重建中。2011年，Lingala等［12］提出了一种重建动态核磁共振MRI图像的新方法，该方法在由欠采样的原始K空间数据进行信号重建时，充分利用了信号的稀疏性。

2.3 三维图像重构

传统的三维磁共振图像重建主要通过在重建中使用适当的约束正则项，并利用了图像序列的时间相关性来获取重建结果。而Montefusco等［13］采用体积图像的梯度稀疏性，将图像重建问题转化为有约束的三维最小化问题，该方法可以用较少的频率采样数据得到高分辨率的重建图像。文献［14］将压缩感知理论应用于大腿肌肉中的磷酸肌醉三维成像，以主成分分析方法为稀疏变换，根据相位编码对图像进行分割，采用k－t稀疏技术的迭代重构算法对图像进行重建。

3 结论

将压缩感知理论应用于医学磁共振成像，可以缩短图像重构时间。而磁共振成像速度越快，重建图像质量越高，越有利于医生的诊断，同时还可以减轻病人在扫描过程中的不适。虽然到目前为止提出了很多不同的针对磁共振成像的稀疏变换、采样轨迹设计、重建算法，但是随着研究的推进和科技的发展，对成像速度和成像质量的要求只会越为越高。因此，寻找最优的稀疏表示、恰当的采样方式以及高质的重建算法依然是我们的目标。而如何将压缩感知与磁共振成像应用的其他方面相结合仍然是我们需要深入研究的问题。

［1］Donoho.Compressed sensing［J］.IEEE Trans on Information Theory，2006，52(4):1289－1300.

［2］Candès E，Romberg J，Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information［J］.IEEE Trans Inf Theory，2006，52(2):489–509.

［3］Lustig M，Donoho D，Pauly J M.Sparse MRI:The application of compressed sensing for rapid MR imaging［J］. Magnetic resonance in medicine，2007，58(6):1182－1195.

［4］练秋生，陈书贞.基于解析轮廓波变换的图像稀疏表示及其在压缩传感中的应用［J］.电子学报，2010，38(6):1293－1298.

［5］Peyre G.Best basis compressed sensing［J］.Signal Processing，IEEE Transactions on，2010，58(5):2613－2622.

［6］Aharon M，Elad M，Bruckstein MA.The K－SVD:An algorithm for designing of overcomplete dictionaries for sparse representations［J］.IEEE Transactions on Signal Processing，2006，54(11):4311－4322.

［7］Ye Xiaojing，Chen Yunmei，Huang Feng.Computational acceleration for MR image reconstruction in partially parallel imaging［J］.Medical Imaging，IEEE Transactions on，2011，30(5):1055－1063.

［8］M.Usman C.Prieto T.Schaeffter，and P.G.Batchelor. k－t group sparse:Amethod for accelerating dynamic MRI［J］.Magnetic Resonance in Medicine，2011，66(4): 1163–1176.

［9］JV Velikina，ALAlexander，A.Samsonov.Accelerating MR parameter mapping using sparsity－promoting regularization in parametric dimension［J］.Magn Reson Med. 2012 Dec published on line.

［10］H.Jung，K.Sung，K.S.Nayak，et al.k－t FOCUSS:A General Compressive Sensing Framework for High ResolutioDynamicMRI.Magn.Reson.Med， 2009， 61: 103－116.

［11］C.Qou，W.Lu，N.Vaswani.Real－Time Dynamic MR Image Reconstruction Using Kalman Filtered Compressed Sensing.IEEE ICASSP，2009:393－396.

［12］Lingala S G，Hu Y，DiBella E，et al.Accelerated dynamic MRI exploiting sparsity and low－rank structure: kt SLR［J］.Medical Imaging，IEEE Transactions on，2011，30(5):1042－1054.

［13］Montefusco Laura B，Lazzaro Damiana，Papi Serena，et al.A fast compressed sensing approach to 3D MR image reconstruction［J］.Medical Imaging，IEEE Transactions on，2011，30(5):1064－1075.

［14］ Prodromos Parasoglou，Li Feng，Ding Xia，Ricardo Otazo，and Ravinder R.Regatte Rapid 3D－Imaging of Phosphocreatine Recovery Kinetics in the Human Lower Leg Muscles with Compressed Sensing Magnetic Resonance in Medicine 68:1738–1746(2012).

Application of compressed sensing in magnetic resonance imaging

ZHONG Xiao－yan1，BU Xiang－lei2，TIAN Hui－yong1
(1Department of biomedical engineering，southern medical university，guangzhou 510515，China; 2Equipment division，guangzhou women and childrens medical center，guangzhou 510263，China)

Compressed sensing is a novel signal acquisition method based on the matrix analysis，probability statistics theory and functional analysis.Original signal can be reconstructed by fewer sampling data that needed in nyquist sampling theory.This paper presents the principles of compressed sensing combined with magnetic resonance imaging(MRI).Sparse representation of magnetic image，design of k－space sampling trace and choice of high quality reconstruction algorithms are included.At last，the other applications of the compressed sensing in the magnetic resonance imaging are discussed.

Compressed Sensing(CS);Magnetic Resonance Imaging(MRI);Sparse representation;Image Reconstruction

R445.2

A

1002－2376(2015)06－0001－05

2015－02－11