基于韦伯-费希纳定律的海水水质富营养化评价——以中街山列岛网箱养殖区为例

许康，徐焕志，王晓艳，胡建坤，陆阿定

(1.浙江海洋学院海洋科学与技术学院，浙江 舟山 316022;2.浙江海洋学院国家海洋设施养殖工程技术中心，浙江 舟山 316022;3.浙江省海洋开发研究院，浙江 舟山 316021)

近年来，随着沿海地区海洋经济的发展和人类海洋活动的不断增加，海水污染日益严重，海洋环境问题日益突出，导致赤潮等富营养化现象日益频发，对沿海的生态环境和养殖捕捞等造成了很大影响。目前形势严峻，沿海各国面临着海水富营养化这一突出问题。现在，海水富营养化问题也深深困扰着我国，我国海岸线漫长，海域面积广阔，各海区水质均受到不同程度的海水富营养影响。根据《2010年中国海洋环境状况公报》［1］发布的数据，2010年我国沿海污染面积严重，仅劣IV类严重污染的海域面积就有约48 000 km2之多。因此，正确评价海水的富营养化程度，对今后的环境治理尤为紧要。

当前，单项指标法、灰色聚类法、富营养化指数法、模糊综合评价法、人工神经网络法等是重要的海水富营养评价方法［2-6］，这些方法各具特点但又存在不足之处。目前为止，有关海水富营养化评估的方法尚未统一。韦伯-费希纳定律(以下简称为W-F定律)，最先应用在心理学和声学方面，将心理量与刺激量以一种对数关系呈现出来［7-9］。近年来，根据其基本涵义，W-F定律已广泛应用于环境质量评价中［10-13］，并得到了合理的评价结果。

本研究首次将W-F定律应用于海水水质富营养化评价中，以中街山列岛海域水质为例，旨在提供一种客观、准确评价海水水质富营养化程度的方法。

1 评价模型

W-F定律作为心理物理学公式，将人类感受强度与外界环境情况刺激强度之间的相关情况进行了定量描述，从而确定出感觉阈限和测量刺激这一物理量和心理学的相关关系［13］57。

W-F定律基本表达式为

式中:k为人体感受的反应量;c作为外界情况的刺激强度;α是韦伯常数。

将W-F定律应用于海水水质富营养化评价，基于以下3点假设:①将外界刺激量c定义为海水某一指标的富营养化质量浓度。②将人体反应量k定义为该指标对人体的影响程度。③α由富营养化指标的性质决定的，对于同一指标α为常数;但在环境质量中，往往涉及多个污染指标，α视为各污染指标的权重［10］37。

基于上述假设，W-F定律函数关系可表示为

式中:kij为i个监测点的第j个水质富营养化指标对人体的危害影响程度;αij为i个监测点的第j个水质富营养化指标的权重;cij为i个监测点的第j个水质富营养化指标的质量浓度标准化值;cij+1的目的是使lg(cij+1)＞0，运用数学的方法证明对结果不存在影响。

1.1 水质富营养化指标权重的确定

通过变异系数的方法，确定水质富营养化指标的权重值。如果某个指标的变异系数较高，则该指标的个体状况差别就会显而易见，因此可以作为评价的主要根据［14］。计算公式［12］114为

式中:cij为在第i个监测点的第j个水质富营养化指标初始测得的水质数据;sj3为第j个水质富营养化指标的海水富营养化三级标准值;p为水质富营养评价过程所选取的水质富营养化指标的个数。数据经标准化处理，消除了量纲对结果的影响。

1.2 综合影响指数ki值的确定

构造综合的评价指数ki，即

式中ki为第i个水质监测点对人体的综合影响指数。ki综合反映了第i个水质监测点外界环境对人体的危害程度，也从侧面反映了环境的优劣［13］58。

基于W-F定律，以水质指标质量浓度作为外界刺激量，以水质富营养化程度作为人体反应程度，来构造海水水质富营养化评价模型，最终确定海水水质富营养化的程度。

2 应用实例

2.1 案例概况

中街山列岛网箱养殖区的海域隶属于舟山渔场分，同时位于中街山列岛国家级海洋特别保护区内［15］。近年，随着人类海上活动的日益频繁，海水养殖业和近海岸工业的崛起，中街山列岛海区内的生态环境日益恶化，水质明显下降，以劣Ⅳ类水质为主［16］。本研究以中街山列岛养殖海域11个调查站点水质为例，进行海水水质富营养化评价研究。监测值、监测站点［15］50分别见表1、图1。

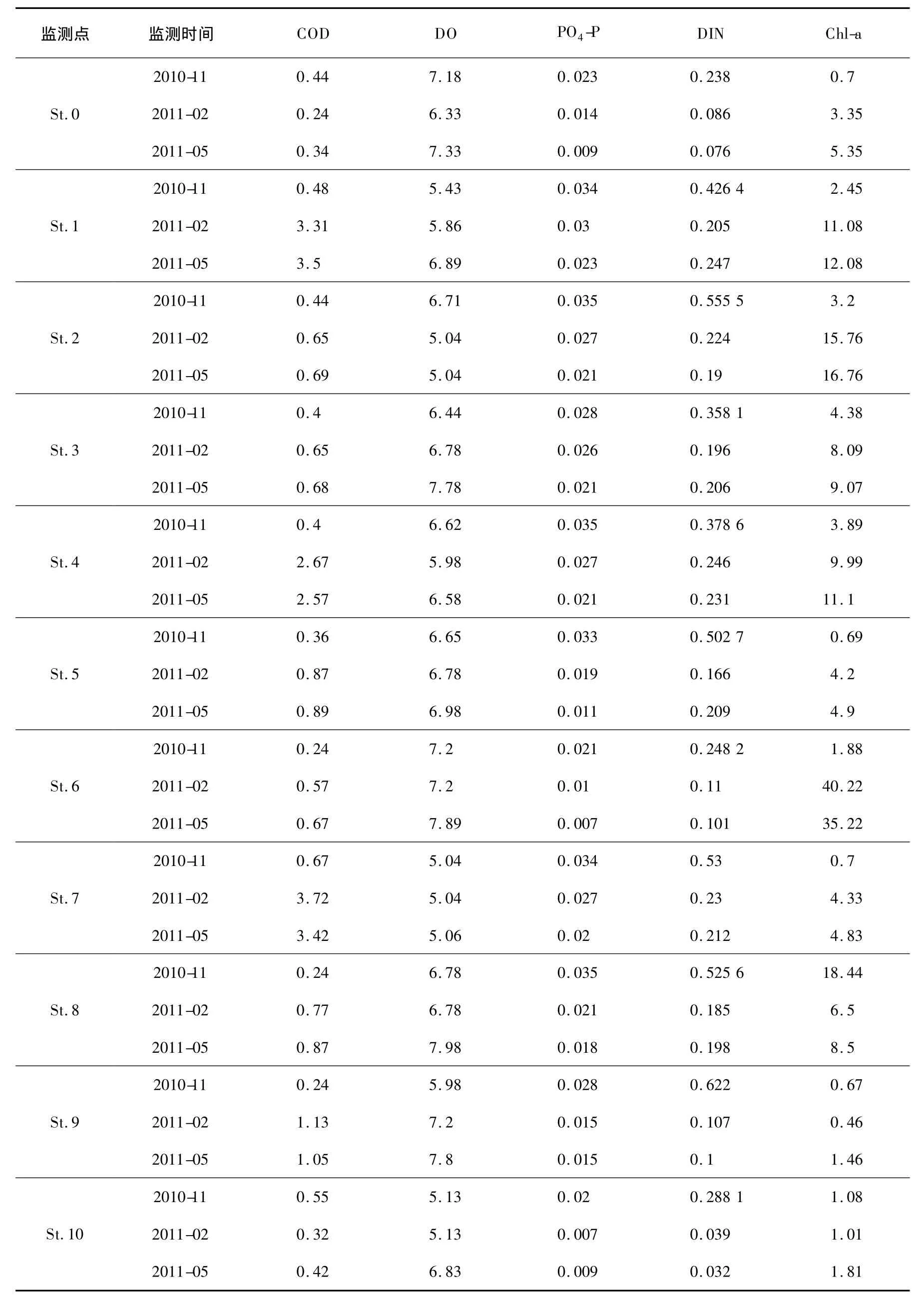
表1 中街山列岛养殖海域11个监测点的监测值 mg·L-1

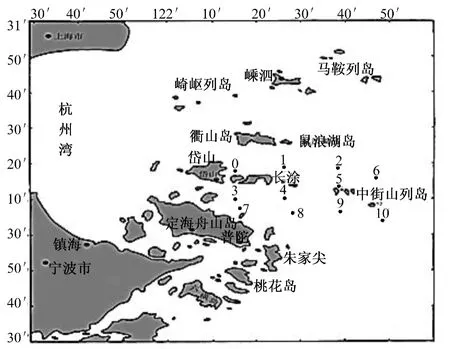
图1 中街山海域调查站位图

2.2 评价标准的确定

以相关性、可操作性和科学性为原则，选取的评价标准有 COD、DIN(总无机氮，NH4-N、NO2-N、NO3-N 之和)、PO4-P、Chl-a、DO。本研究对表层水进行测定，测定方法依据《海洋调查规范》［17］和《海洋监测规范》［18］中的方法进行。参考海水质量标准［19］和文献［20-24］制定的中街山列岛海水富营养评价标准，如表2所示。

根据检测数据选取 COD、DO、DIN、PO4-P、Chl-a等5个指标。将表2中数值进行标准化，其中DO为反向指标，取其倒数进行计算，其标准化的结果见表3。针对表3的数值，根据式(2)～(4)计算ki值，确定海水富营养化等级与ki值得对应关系:ki≤0.189为第Ⅰ类贫营养级;0.189＜ki≤0.256为第Ⅱ类中营养级;0.256＜ki≤0.301为第Ⅲ类富营养级。

表2 海水富营养化评价标准 mg·L-1

表3 海水富营养化标准数值标准化结果

2.3 评价结果

对表1中的检测数据按表3的标准化结果进行标准化，再按照上述公式，经计算得出中街山列岛网箱养殖海域各监测站点的综合影响指数值，从而根据海水富营养化等级标准对应的ki值分级确定各监测点的海水富营养化等级，并与富营养化指数法［25］的评价结果进行比较，2种方法的评价结果及比较见表4。

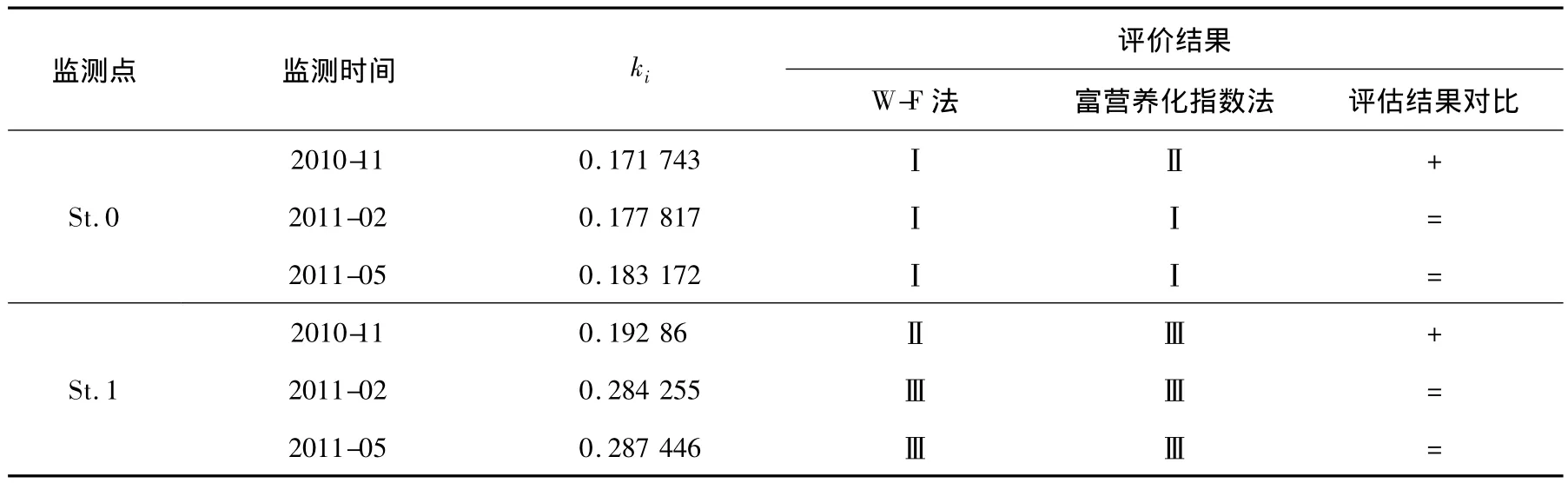
表4 W-F法和富营养化指数法的评估结果对比

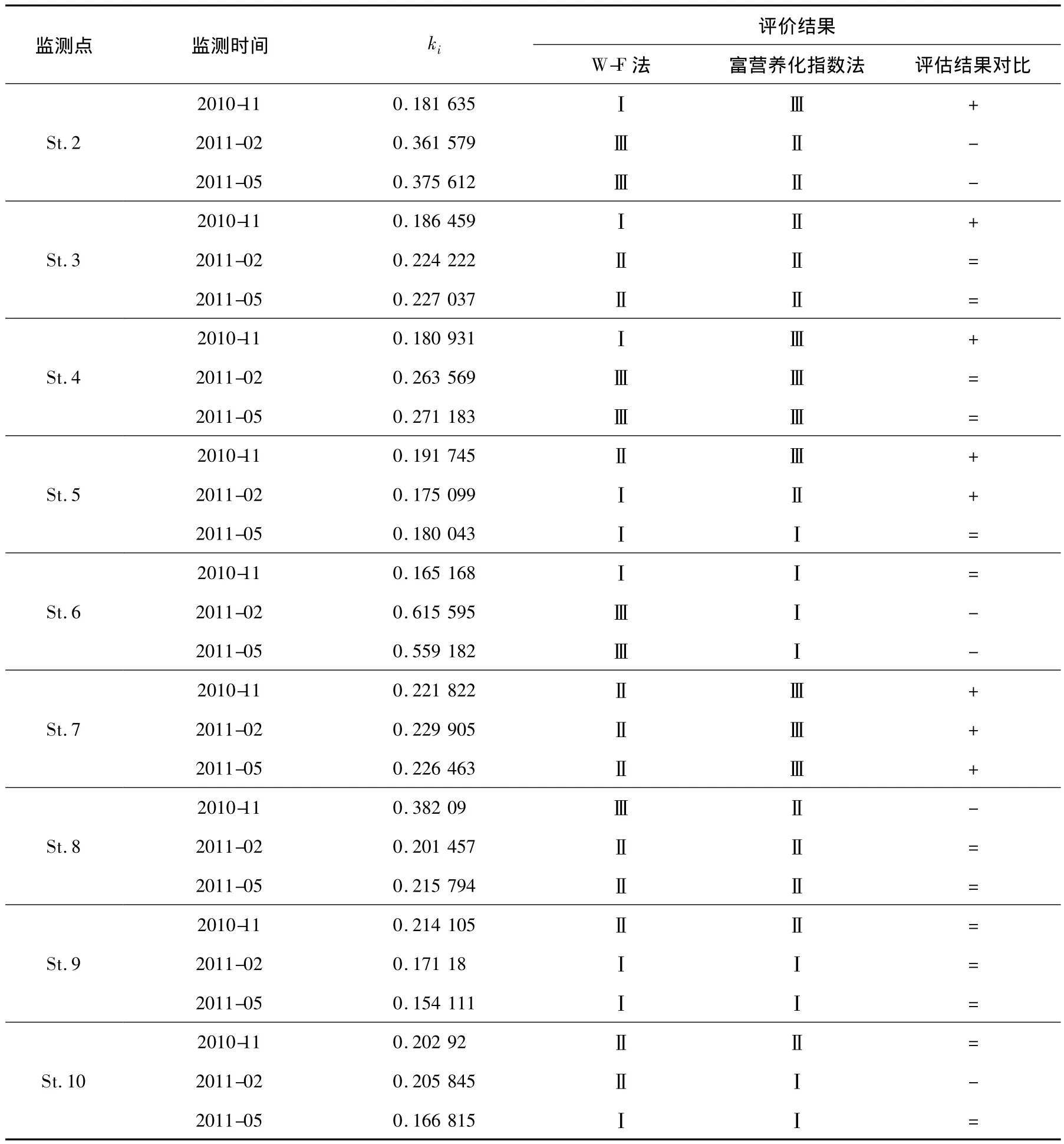
表4(续)

3 结果与讨论

由表4可知，本研究应用 W-F定律评价2010—2011年中街山列岛养殖海域11个站点、3个航次的海水富营养化状况。比对富营养化指数法与W-F定律评价法结果，两者既存在相同之处，又有差异。通过表4分析可得:监测的11个站点的33个样品中，有17个(51.52%)样品的分析结果一致;10个(30.30%)样品的分析结果显示W-F评价的水质等级优于富营养化指数法;其余6个(18.18%)的W-F水质评价等级劣于富营养化指数法。

2种评价方法评价结果都显示中街山列岛养殖海域在2010、2011年海水水质富营养化相对严重，尤其是st.1和st.4监测点海水富营养化最为严重;2010、2011年，st.11监测点经2种评价方法得出的评价等级相同;与2010年相比，2011年8个监测点的海水水质富营养化更为严重。

在W-F法评价等级劣于富营养化指数法的6个水样，评价结果差异最大的是2011年2月、5月的st.5监测点，与富营养化指数法相比，相差2个评价等级，W-F评价等级均显示为等级Ⅲ，富营养化指数法均显示为等级Ⅰ。根据水质指标的质量浓度具体分析得出，Chl-a浓度超过海水富营养化标准(见表2)3～4倍，因富营养化指数法未考虑Chl-a的影响，故W-F法评价该水样的等级为Ⅲ较合理。

在W-F法评价等级优于富营养化指数法的10个水样中，评价结果差异最大的为2010年11月st.2、st.4监测点的水样，W-F评价法均显示等级为Ⅰ，富营养化指数法均显示等级为Ⅲ。针对具体水质指标分析，除DIN、PO4-P 2项指标的质量浓度超过等级Ⅲ，Chl-a指标质量浓度略微超过等级Ⅰ，其余2项指标均符合等级Ⅰ，DIN、PO4-P 2项指标对富营养化指数法的评价影响比较大。因此综合分析，W-F法评价的水样等级为Ⅰ较客观准确。

经过实例应用结果表明，W-F法用于海水富营养化评价是可行的、科学合理的，能较好地反映中街山列岛富营养化的真实水平，可为海水富营养化监控提供有效的科学依据。

［1］国家海洋局.2010年中国海洋环境状况公报［R/OL］.(2011-05-13)［2015-08-10］.http://www.gov.cn/gzdt/2011-05/13/content_1863357.htm

［2］日本机械工业联合会，日本产业机械工业会.水域的富营养化及其防治对策［M］.杨祯奎，译.北京:中国环境科学出版社，1987:271.

［3］郭卫东，章小明，杨逸萍，等.中国近岸海域潜在性富营养化程度的评价［J］.台湾海峡，1998，17(3):64-70.

［4］王冬云，黄焱歆.海水富营养化评价的人工神经网络方法［J］.河北建筑科技学院学报，2011，18(4):27-29.

［5］BRICKER S B，FERREIRA J G，SIAMS T.An integrated methodology for assessment of estuarine tropic status［J］.Ecol Modell，2003，169:39-60.

［6］时文博.我国近岸海水富营养化现状及评价方法的研究探讨［J］.河北渔业，2012(4):42-46.

［7］DRÖSLER Jan.An n-dimensional weber law and the corresponding fechner law［J］.Journal of Mathematical Psychology，2000(44):330-335.

［8］COBB P W.Weber's law and the fechnerian muddle［J］.Psychological Review，1932，39(6):533-551.

［9］URBAN F M.The Webber-fechner law and methal measurement［J］.Journal of Experimental Psychology，1933，16(2):221-238.

［10］李小燕，王菲凤，张江山.基于韦伯-费希纳定律的湖泊富营养化评价［J］.水电能源科学，2011，29(3):37-39.

［11］李祚泳，彭荔红.基于韦伯-费希纳定律的环境空气质量标准［J］.中国环境监测，2003，19(4):17-19.

［12］廖文珍，王菲凤，张江山.基于韦伯-费希纳定律的海域水质综合评价［J］.海洋环境科学，2014，33(1):111-117.

［13］薛文博，易爱华，张增强.基于韦伯-费希纳定律的一种新型环境质量评价法［J］.中国环境监测，2006，22(6):57-59.

［14］李因果，李新春.综合评价模型权重确定方法研究［J］.辽东学院学报(社会科学版)，2007，9(2):92-97.

［15］阳丹，陈应华，吴常文.中街山列岛及其邻近海域海水质量评价［J］.浙江海洋学院学报，2012，31(1):49-53.

［16］郑莉，张进.长山群岛周边海域水质监测分析［J］.水产科学，2000，19(3):33-35.

［17］中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.海洋调查规范:GB/T 12763—2007［S］.北京:中国标准出版社，2007.

［18］中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.海洋监测规范:GB/T 17378—2007［S］.北京:中国标准出版社，2008.

［19］张自杰.排水工程:下册［M］.北京:中国建筑工业出版社，2000.

［20］彭云辉，王肇鼎.珠江河口富营养化水平评价［J］.海洋环境科学，1991，10(3):7-13.

［21］林辉，张元标，陈金民.厦门海域水体富营养程度评价［J］.台湾海峡，2002，21(2):154-161.

［22］郝建华，霍文毅，俞志明.胶州湾增养殖海域营养状况与赤潮形成的初步研究［J］.海洋科学，2000，24(4):37-41.

［23］高玉荣.北京4海藻类群落结构特征与水体营养水平的研究［J］.生态学报，1992，12(2):173-179.

［24］况琪军，夏宜铮.太平湖水库的浮游藻类与营养型评价［J］.应用生态学报，1992，3(2):173-179.

［25］何桐，谢建，方宏达，等.大亚湾海域春季营养现状分析与评价［J］.海洋环境科学，2008，27(3):221-224.