基于Rogowski线圈动态性能的结构、电磁参数研究

2015-01-15刘冬梅李泽滔王炳昱

现代机械 2015年1期

刘冬梅，李泽滔，王炳昱

(贵州大学电气工程学院，贵州贵阳 550025)

0 引言

随着电力系统自动化和智能化的提高以及发、输电容量的增大，传统的电磁式互感器由于受外界环境的影响较大、测量精度低，于是电子式电流互感器便应运而生，Rogowski线圈电流互感器作为一种新型的电子式互感器［1］，它结构简单、线性度好、体积小、精度较高、不受被测电流大小的限制，能和电子测量装置联机使用，所以对其进行研究有重要意义。

Rogowski线圈结构、电磁参数对其动态性能的精确性与准确性影响较大，本文通过建立相应模型的传递函数，选取合适的参数，对不同结构、电磁参数的仿真结果进行比较即时域和频域特性曲线，进而得出结构、电磁参数对其性能影响的规律，并提出优化方法。

1 Rogowski线圈的测量原理

Rogowski线圈结构示意图如图1所示，是将漆包线均匀的缠绕在一个环形绝缘骨架上。将被测的一次侧母线放在中心，根据被测电流i的变化感应出二次侧的感应电动势e(t)，然后根据相应信号处理得出i值。

Rogowski线圈测量电流的依据是安培环路定律与电磁感应定律［2］。

图1 Rogowski线圈结构示意图

Rogowski线圈的感应电动势为:

其中，i为一次电流;μ0为真空磁导率;h为骨架高度;n为绕线匝数;a为骨架内径;b为骨架外径。

由等效电路图［3-4］，可得:

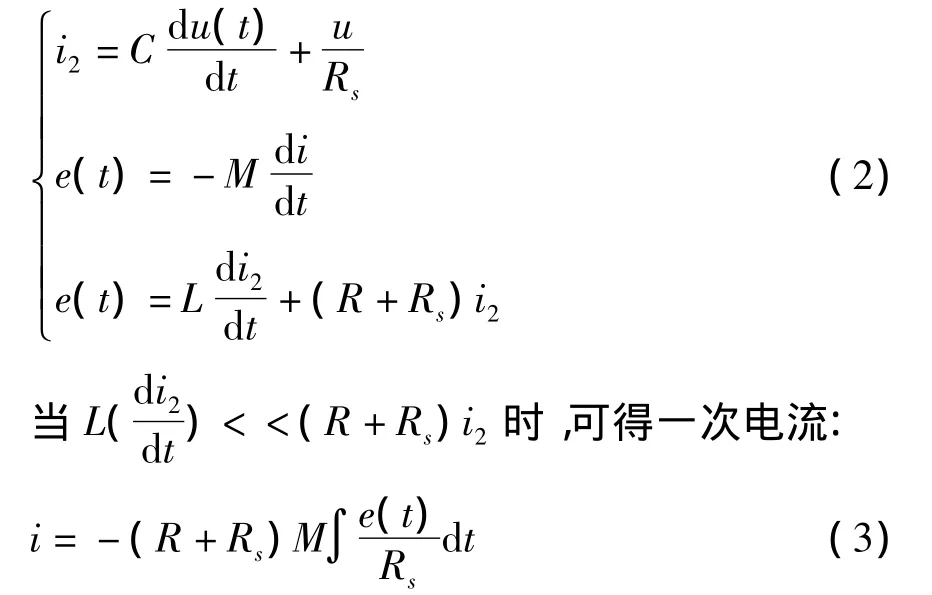
其中R、Rs分别为线圈内阻和采样电阻，采样电压为u，由式(2-3)可得，罗氏线圈相当于一个微分环节，为了使输出信号还原成被测电流，必须后加一个积分环节。

2 结构参数对罗氏线圈的动态特性影响

2.1 不同截面形状的传递函数

分析罗氏线圈结构参数对其动态性能的影响有利于提高测量的精确性与准确性，通过建立传递函数，选取合适的参数，对不同结构参数的仿真结果进行比较即时域和频域特性曲线，进而得出结构参数对其性能影响的规律，提出优选方法。

Rogowski线圈一般是将导线密绕在骨架上的，骨架截面一般分为多种形状，而本文仅对圆形和矩形线圈进行研究。其结构如图2。

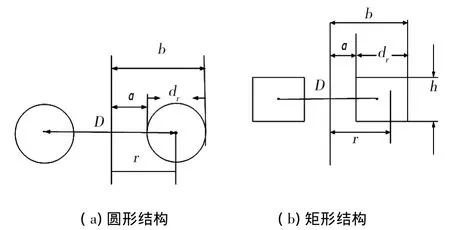
图2 不同的骨架截面结构图

假设初始条件为零，将式(2)进行拉氏变换后，得到其传递函数为:

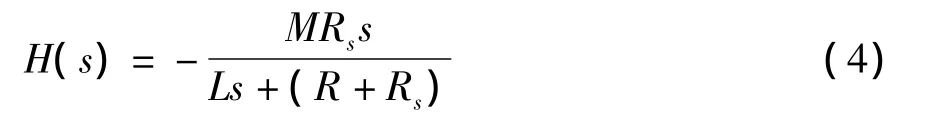
(1)圆形截面［5］

罗氏线圈为圆形截面结构，如图2(a)，图中D=2r为中心直径，dr为截面直径，真空磁介质常数为μ0=4π×10-7(H/m)，而铜导线的电阻率为ρ=0.018 51 Ω·mm2/m。则可得电动势为［6］:

圆形截面的互感为:

推出线圈的内阻为:

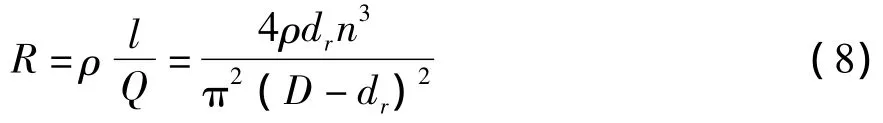
将式(6)-(8)代入式(4)中，得传递函数为［7］:

(2)矩形截面［8］

罗氏线圈为圆形截面结构，如图2(b)，b、a、h为线圈的外径、内径和高，则电动势为:

矩形截面的互感为:

线圈的内阻为:

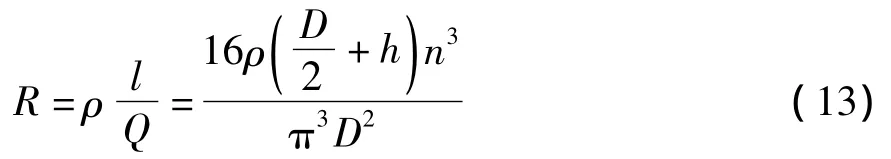
将式(7)、(12)、(13)代入式(4)中，则同理可得:

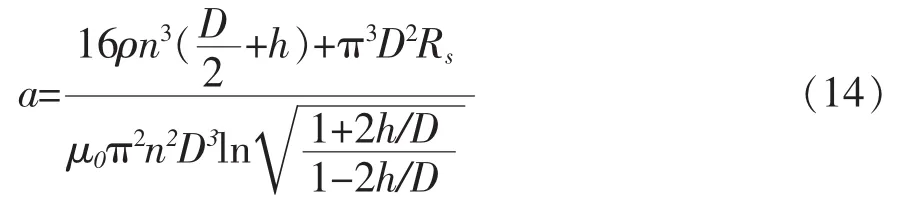
以下，将以测量的线圈骨架的直径D=0.15 mm，Rs=150 Ω为例，分别对不同线圈形状，不同的结构参数d、n值，进行MATLAB仿真实验，观察阶跃响应及幅频、相频曲线，分析性能变化规律，得出更好的优化结构参数。

2.2 不同线圈截面形状仿真研究

图3为圆形和矩形两种截面下，选取n为1 600匝，d，h均为0.04 m的阶跃响应和Bode图。

图3 不同截面形状的阶跃、Bode图

从仿真结果可以看出，圆形截面的线圈比正方形截面的线圈的动态性能好，实际应用中，应根据实际情况以及被测电流特点，合理选取截面形状，以取得较好的动态性能。

2.3 不同线圈截面直径仿真分析

图4n为1 600匝，截面直径 d分别选取为0.018 m、0.024 m、0.03 m三种情况的阶跃响应以及幅频相频特性曲线。

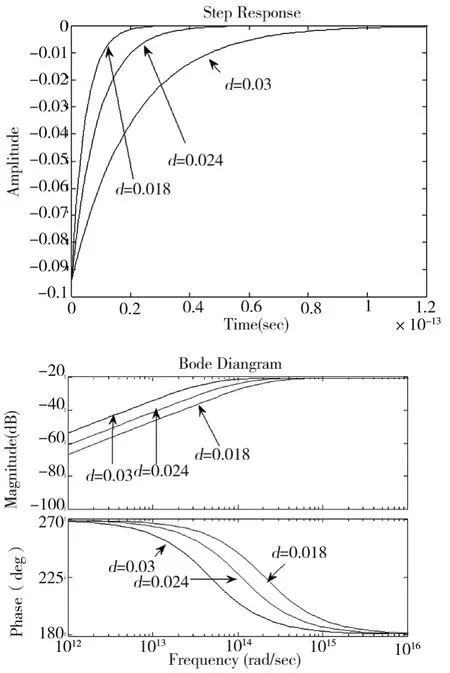
图4 不同截面直径的阶跃、Bode图

从图中可以看出:随着d的增大，阶跃响应的上升时间变长，系统达到稳定所需的时间也变长，响应速度越慢。从Bode图中可以看出，d越大，系统对高频信号反应越迟钝。但是，在实际中d太小就会使骨架面积很小，减弱了骨架的刚性，增大了加工的难度，建议选取d为0.018 m。

2.4 不同线圈匝数仿真分析

如图5，当 d=0.018时，选取 n为1 200、1 600、2 000时可以看出匝数n越大，上升时间越长，响应速度也越慢，系统的灵敏度也低。但是线圈的匝数越多，与磁场交链总的有效面积就越大，感应信号也就越强烈。在相同的骨架上缠绕的线圈匝数越多，所采用漆包线的直径就越小，所需的加工工艺就越高，所以应合理选取，建议选取1 600。

2.5 优化结构参数分析

图5 不同截面匝数的阶跃、Bode图

从以上仿真结果中可以看出，线圈的结构参数直接影响线圈的动态性能，随着d的减小以及n的减小，系统的动态性能越好。所以，在选取线圈的结构参数时，线圈截面直径在条件允许的情况下应尽可能的取小，同时，应选取较细的导线进行密绕，使得n适宜。从而减小阶跃响应上升时间，提高系统的灵敏度。为了明显的验证规律，选取d=0.018，n=160 0和d=0.03，n=1 200两种情况进行仿真比较，结果如图6。

图6 线圈优化前后的阶跃、Bode图

本小节主要通过对Rogowski线圈的结构参数的仿真研究，得到线圈的截面形状，截面直径，以及线圈匝数对线圈的动态性能的影响规律，并通过优化结构参数前后的仿真比较，验证了规律。根据对线圈性能的要求的侧重点的不同，如反应精度、速度、输出增益等选择线圈的结构参数，简化了线圈的设计过程，提高设计效率。

3 电磁参数对罗氏线圈的动态特性影响

为了研究电磁参数对其动态性能的影响，利用上面得到的结构参数，以圆形截面为例，通过传递函数，利用MATLAB仿真软件得到不同的电磁参数时线圈的阶跃响应以及幅频特性与相频特性曲线，详细分析了分布电容、取样电阻、线圈内阻对Rogowski线圈的动态性能的影响，对于设计有良好的动态性能的罗氏线圈有一定的指导意义。

3.1 传递函数建立

将方程组(2)进行拉普拉斯变换，得到其传递函数［9］为:

3.2 不同分布电容仿真分析

线圈的互感M=0.07 μH，自感L=86 μH，内阻R0=4 Ω，取样电阻Rs=150 Ω，分别做出分布电容为1.2 nF，3.6 nF，7 nF时的阶跃响应曲线以及Bode图，如图7所示。

从图7(a)可以看出，分布电容C0的值越大，阶跃响应上升时间越长，并且有振荡现象出现，响应速度越慢，稳定的时间越长。分析图7(b)中可知，随着分布电容的增大，高频的截止频率降低，线圈高频特性变差。在实际应用中，应合理设计线圈的结构参数，尽可能的减小分布电容。

图7 不同分布电容的阶跃、Bode图

3.3 不同取样电阻仿真分析

图8中，取线圈的互感M=0.07 μH，自感L=86 μH，内阻 R0=4 Ω，分布电容 C0=1.2 nF，取样电阻分别取100 Ω、150 Ω、200 Ω 做出线圈的阶跃响应以及幅频与相频曲线。

分析阶跃响应曲线可知，取样电阻越大，阶跃响应的上升时间越短，但是有振荡现象出现，稳定的时间会变长。从Bode图可以看出，取样电阻越大，高频截止频率提高，线圈高频特性得到了改善。所以在实际应用中，要结合多方面的因素合理选择。

3.4 不同线圈内阻仿真分析

图9中，取线圈的自感为L=86 μH，互感为M=0.07 μH，取样电阻 Rs=150 Ω，分布电容 C0=1.2 nF，分别取线圈内阻 R0为 0.3 Ω、3.5 Ω、9 Ω 做出阶跃响应以及Bode图。

从图9中可以看出，线圈内阻的变化对阶跃响应的上升时间及幅频相频特性基本上没影响，仅仅对阶跃响应的稳定值有些影响。所以要想靠改变线圈的内阻改善线圈的动态性能意义不大。

图8 不同取样电阻的阶跃、Bode图

图9 不同线圈内阻的阶跃、Bode图

3.5 优化电磁参数分析

从以上可看出，Rogowski线圈的动态性能直接受到电磁参数的影响，且不同的电磁参数对其性能的影响程度不相同。在制作Rogowski线圈过程中要尽量减小分布电容，同时要使用电阻率小的绕线材料来减小线圈的内阻，取样电阻要满足最佳阻尼比，使罗氏线圈达到最好的动态特性，为了验证上述规律，选取 R0=4 Ω，C0=7 nF，Rs=200 Ω 和 R0=3.5，C0=1.2 nF，Rs=150 Ω

两种情况做比较，其阶跃响应以及幅频、相频特性曲线如图10。