一种具有仿射不变性的倾斜影像快速匹配方法

肖雄武，郭丙轩，李德仁，赵 霞，江万寿，胡 翰，张春森

1.武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉430079；2.西安科技大学测绘科学与技术学院，陕西 西安710054

1 引 言

由于三维重建需要获取侧面纹理信息，倾斜摄影技术应运而生。然而，由于倾斜影像的局部仿射变形大、存在色差等问题，给影像匹配带来了很大困难。

在匹配领域，基于像方搜索和基于物方搜索是两个不同的研究方向。目前针对大倾角倾斜影像匹配，基于像方搜索思路的匹配方法主要有如下3种：

（1）对原始影像提取具有仿射不变性的区域，建立描述子，进行匹配。MSER［1］、Harris－Affine ＆Hessian－Affine［2－3］在这类算法中表现最好［4］，但均不具备完全仿射不变性［5］，对大倾角倾斜影像的匹配效果不好。

（2）对原始影像先进行粗匹配（一般利用SIFT［6］或MSER算法及比较严格的匹配策略），得到匹配点对，利用最小二乘法或RANSAC算法［7］计算出两幅影像之间的一个关系矩阵H。以影像B为参考影像，利用H矩阵对影像A进行DLT变换得到校正影像A′。对校正影像A′和影像B进行SIFT匹配，得到匹配点对，再将校正影像A′上匹配出的特征点反算到原始影像A上。该思路被广泛采用［8－10］，但是由于该方法的粗匹配点对可能会存在数量过少、分布不均匀、正确匹配率不高等问题，计算的H矩阵不一定准确，所以难以保证匹配效果。

（3）模拟法。ASIFT［5，11］采用近似于穷举法来模拟相机轴定向参数，然后应用SIFT模拟尺度、规范化位移和旋转，具备完全的仿射不变性，与 SIFT、MSER、Harris－Affine＆Hessian－Affine相比，在对图像错切、旋转、尺度、光照变化上具有更强的鲁棒性［5，12］，在目标检测与识别、二维图像匹配、立体匹配、三维重建等方面应用广泛［13－15］。尽管ASIFT对倾斜影像的匹配效果较好，但其计算复杂度高、效率比较低下，难以满足实际的应用需求［16］。在基于物方搜索思路方面，文献［17—18］提出了物方空间引导的多像多基线匹配方法，并较为成功地应用到PixelGrid系统中。

针对上述基于像方搜索思路存在的问题，考虑利用纠正影像匹配后再反算到原始影像的思路以确保匹配效果，但是要保证用尽可能少的次数得到合理的纠正影像。因此，本文融合物方和像方方法（假设物方的方向，在像方进行搜索），采取ASIFT算法的逆向思路（ASIFT做仿射变换，本文作其逆变换），提出了一种较为快速的大倾角倾斜影像匹配方法，先估算影像的相机轴定向参数，计算出初始仿射矩阵，再通过一次逆仿射变换得到纠正影像，对纠正影像进行SIFT匹配。为了得到较为密集、均匀的同名点对，通过一定的方法尽量保留最邻近匹配点集中的正确匹配点对，并有效地剔除误匹配。对三组典型的倾斜影像数据进行匹配试验，试验结果表明本文算法得到的匹配点对在数量和分布情况、准确率、尤其是效率上要优于ASIFT算法。

2 五倾斜影像获取平台

采用中国测绘科学研究院刘先林院士团队研制的SWDC－5倾斜相机平台获取倾斜影像。图1是SWDC－5相机平台，表1是SWDC－5的部分平台参数。

图1 SWDC－5倾斜相机平台Fig.1 The camera platform of SWDC－5

表1 SWDC－5各相机之间的相对角元素Tab.1 The relative angular elements between the cameras of SWDC－5

该平台可通过IMU设备获得E相机摄取影像（即下视影像）的粗略角元素（φE、ωE、κE）。

3 倾斜影像快速匹配方法

3.1 仿射摄像机模型

由于使用计算机对透视投影进行模拟和处理计算复杂度高、比较复杂，对于地势比较平坦的城市区域，局部透视投影可以使用仿射变化来估计［5］。

定理［5］：设某一仿射映射其行列式为正，且不存在相似矩阵，则其存在唯一的分解

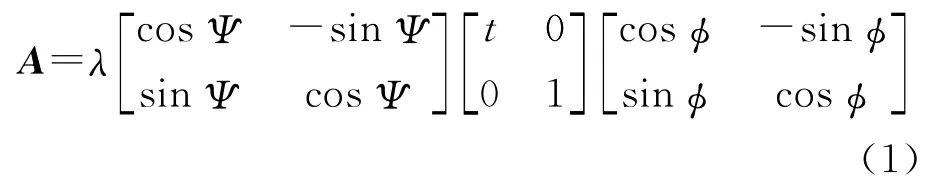
如图2，式（1）可按相机运动解释如下：

平面u代表某一平坦的地物表面，右上角平行四边形代表朝向u的相机；参数θ和φ为相机轴定向参数，分别称为相机的经度和纬度；t＝为斜度；ψ代表相机绕其自身光轴旋转的角度；λ代表缩放倍数。

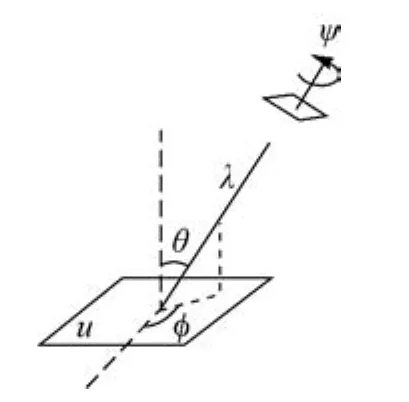
图2 仿射相机模型Fig.2 The affine camera model

3.2 基于仿射不变的倾斜影像匹配方法

3.2.1 计算初始仿射矩阵

根据每张影像的旋转矩阵R计算相机轴定向参数：纬度角θ∈［0°，90°）和经度角φ∈［0°，180°），再计算初始仿射矩阵。

（1）计算每张影像的旋转矩阵R

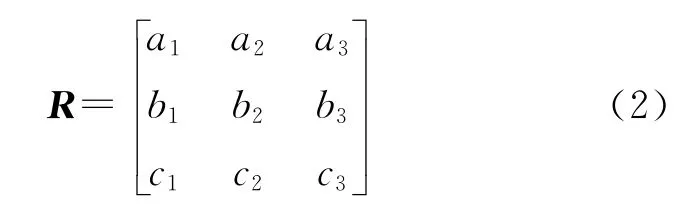
式中，a1＝cosφcosκ－sinφsinωsinκ；a2＝－cosφsinκ－sinφsinωcosκ；a3＝－sinφcosω；b1＝cosωsinκ；b2＝cosωcosκ；b3＝－sinω；c1＝sinφcosκ＋cosφsinωsinκ；c2＝－sinφsinκ＋cosφsinωcosκ；c3＝cosφcosω。

由式（2），利用下视影像的粗略角元素（φE，ωE，κE）计算下视影像的旋转矩阵RE。利用下视相机与各侧视相机之间的相对姿态（φE－i，ωE－i，κE－i）计算同一摄站下视影像与侧视影像的相对旋转矩阵RE－i。

由下视影像的旋转矩阵RE、同一摄站下视影像与侧视影像的相对旋转矩阵RE－i计算该摄站各张侧视影像的旋转矩阵Ri。

（2）利用每张影像的旋转矩阵R计算tiltswing－azimuth（t－s－α）坐标系统的3个角度［19］

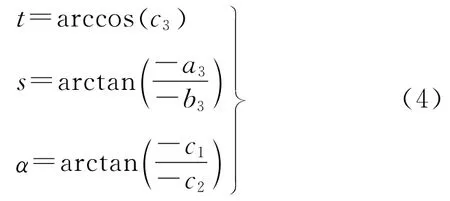
式中，s、α∈［－180°，180°］。

（3）计算相机轴定向参数

（4）计算初始仿射矩阵

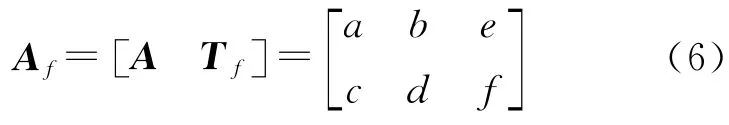
式中

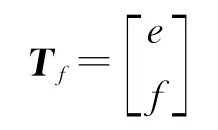
由于SIFT算法具有尺度和旋转不变性，因此，本文将尺度参数λ设为1，旋转参数Ψ设为0。在此，将（e，f）的坐标设为（0，0），后面通过计算平移矩阵Tm将纠正影像移动到适当位置。

3.2.2 计算纠正影像

在计算出仿射矩阵后，对原始影像进行逆仿射变换，得到纠正影像（近视正射影像）。

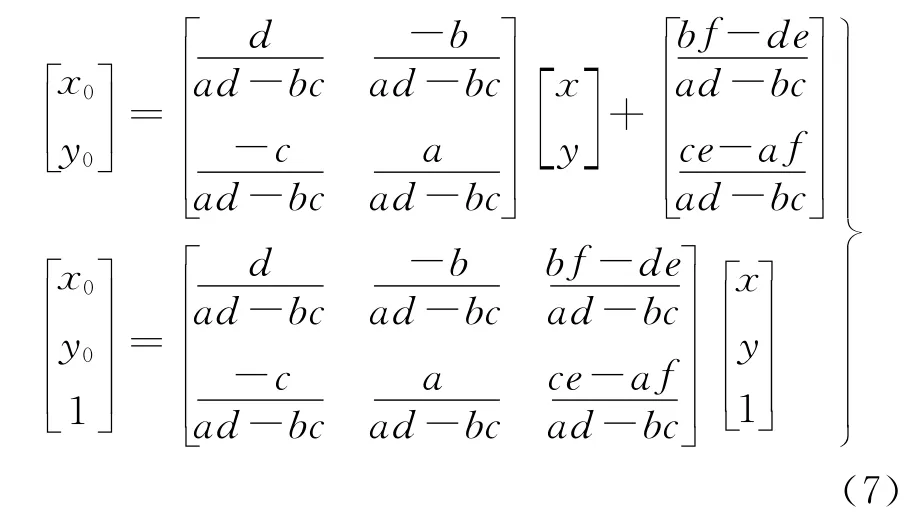
由式（7）可得

式中

在式（8）中，I表示原始影像；I′表示得到的纠正影像（近视正射影像）。

为了不浪费存储空间，需要计算纠正影像的适当大小和平移矩阵Tm，将纠正影像移动到恰当位置，如图3。

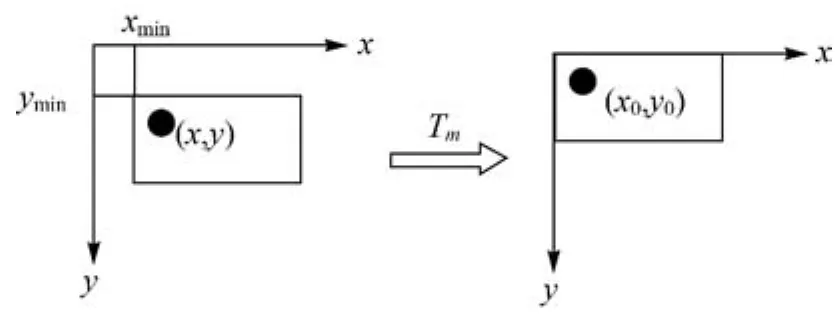
图3 对纠正影像做适当的平移Fig.3 To make a appropriate translation to the rectified image

利用影像I（宽度为W0、高度为H0，单位：像素）的4个角点和矩阵计算纠正影像I′的4个角点。

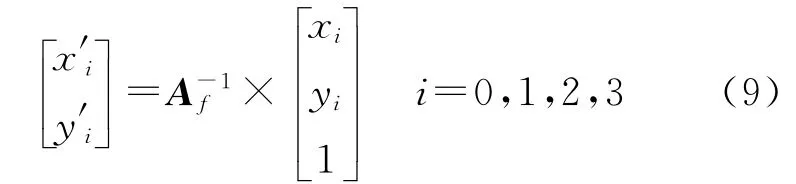
式中，（x0，y0）＝（0，0）；（x1，y1）＝（W0，0）；（x2，y2）＝（0，H0）；（x3，y3）＝（W0，H0）。

计算纠正影像I′的大小（宽度为Xmax－Xmin、高度为Ymax－Ymin）和平移矩阵Tm

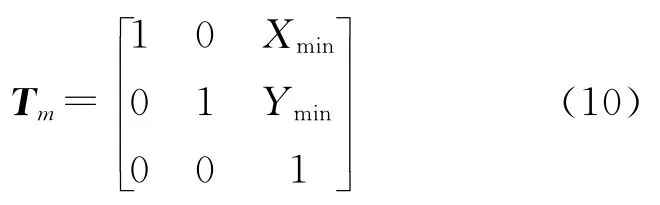
计算经过适当平移后的仿射矩阵Aft

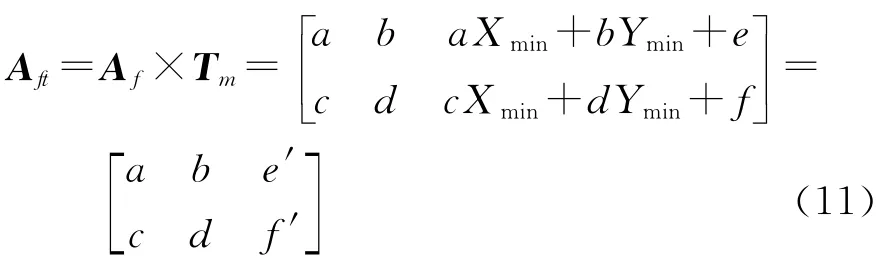
Aft的伪逆矩阵可以表示为

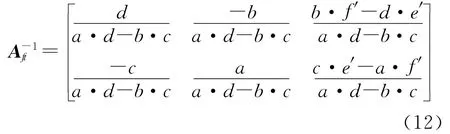
因此

在式（13）中，I表示原始影像表示经过适当平移后的纠正影像。也就是说，纠正影像I′中的坐标（Xmin，Ymin）对应纠正影像I′0中的坐标（0，0）。

文中仅需对原始影像作一次逆仿射变换。原始影像与纠正影像的局部效果对比，如图4。

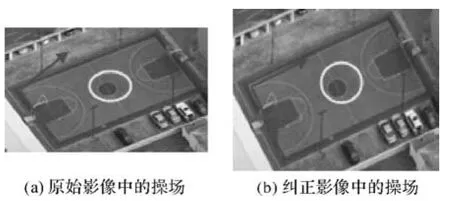
图4 影像纠正前、后的局部效果对比Fig.4 The comparison of the same local area to the original image and the rectified image

3.2.3 在纠正影像上进行匹配

为了得到较为密集、均匀的正确匹配点对，考虑对最邻近匹配点集剔除误匹配。然而，利用RANSAC算法剔除误匹配时，要保证粗匹配点对中包含至少近50%的正确同名点对［6］。因此，本文采用如下匹配策略作为替代办法，解决上述问题。

（1）特征提取及描述。对两张纠正影像分别提取DoG特征点并建立SIFT描述子。

（2）粗匹配。匹配时，采用比值提纯法（NNDR，次邻近距离与最邻近距离的比值小于0.85）［6］、归一化互相关（NCC）测度约束［20］，ai和bi分别为匹配点对两个描述向量的元素，a和分别为两个描述向量各元素的平均值，γ（a，b）＞0.6）和左右一致性检验（先由左片中特征点搜索右片中满足条件的同名点，得到匹配点集S1；再由右片中特征点搜索左片中满足条件的同名点，得到匹配点集S2；最终的匹配点集是S1和S2的交集。该方法可在近乎不减少正确匹配点对的同时，有效剔除一些误匹配）得到粗匹配点对。

（3）计算F、H矩阵和主方向的平均差值δθ。由粗匹配点对，利用RANSAC算法（容差为3个像素）分别计算出两幅影像之间的基本矩阵F和单应矩阵H［7］。由利用RANSAC算法对粗匹配点计算H矩阵的内点来计算匹配点对主方向差值的平均值，θi和为匹配点对的主方向角度值，n为内点个数。

（4）重新匹配。对SIFT描述子重新进行最邻近匹配，利用极线约束［7］，其中和为的前两个元素，xi和为匹配点对，εf＜4）、单应矩阵约束［7］测度约束［20］和主方向差值一致性约束（即待匹配点与其最邻近特征点的主方向差值应与δθ较接近不超过10°）剔除误匹配，得到匹配点对。

3.2.4 反算匹配点对将纠正影像上的匹配点对反算到原始影像上

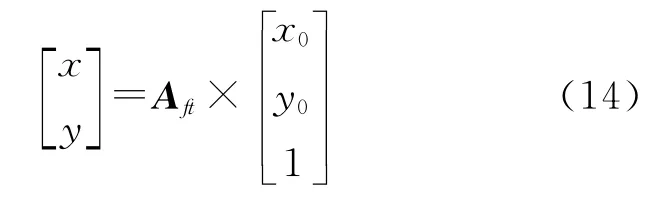
式中，（x0，y0）表示纠正影像上的点；（x，y）为原始影像上的对应点。

由于在纠正影像有纹理信息区域的边界上可能产生少量的误匹配点对，因此剔除落在原始影像边界20像素以内的匹配点对。

4 试验与分析

系统环境：Windows 7，8GB RAM，i7CPU。试验数据：广东阳江地区的一组倾斜影像数据（如图5），侧视影像（4092像素×3057像素）的倾角约为45°，下视影像（4103像素×3039像素）的倾角约为5°。这一组影像的粗略角元素（φ，ω，κ），如表2。点对，由重叠误差［4，22］是特征点对的描述区域的面积或像素个数。若εS＜0.5，则为正确匹配点对）来判定。

表2 4张倾斜影像数据的粗略角元素Tab.2 The rough angular elements of the oblique images

图5 试验数据：4张典型的倾斜影像Fig.5 The experimental data：four typical oblique images

（2）匹配点对的正确率，即正确匹配点对数量与匹配点对总量的比值。

4.1 AIF算法的匹配效果

分别用SIFT、ASIFT、AIF算法对下视相机与侧视相机获取的影像（如将下视影像与后视影像记为第1组）、两个相邻相机获取的侧视影像（如将后视影像与右视影像记为第2组）、两个相离相机获取的侧视影像（如将左视影像与右视影像记为第3组）这3组有代表性的数据进行匹配，对比和分析试验结果。

SIFT算法采用常规、有效的匹配策略：比值提纯法（阀值0.7），并利用RANSAC算法剔除误匹配［6，21］。由于 ASIFT算法在图像重复纹理区域会产生一些误匹配，故本文先利用ASIFT算法获得粗匹配点对，再利用RANSAC算法提纯匹配点对。

对试验结果的评价标准：

（1）正确匹配点对的数量及分布。由于3种匹配方法得到的匹配结果都采用RANSAC算法进行提纯（SIFT和ASIFT直接采用RANSAC算法，AIF相当于间接采用RANSAC算法），故3种方法得到的匹配点对均满足单应矩阵约束。对于每组数据，在影像重叠区人工选取12对均匀分布的检测点，并利用最小二乘法计算出两幅影像之间的单应矩阵H0。匹配点对是否为正确匹配点对，由重叠误差是特征点对的描述区域的面积或像素个数。若εS＜0．5，则为正确匹配点对）来判定。

（2）匹配点对的正确率，即正确匹配点对数量与匹配点对总量的比值。

3种匹配方法对这3组数据的匹配效果如图6，对3组数据的匹配结果统计如表3。由图6和表3可知：对于第一组数据，在正确匹配点对数量及分布上，本文算法要明显优于SIFT和ASIFT算法；在匹配正确率上，3种方法的正确率都比较高，本文方法略优于SIFT和ASIFT算法。对于第2组数据，SIFT算法匹配失败，本文算法在正确匹配点对数量上要优于ASIFT算法；在点对分布和正确率上，要略优于ASIFT算法。对第3组数据，3种方法的匹配效果都比较好；在匹配点对数量、准确率、尤其是分布上，本文方法和ASIFT算法均要优于SIFT算法；虽然ASIFT算法的正确匹配点对数量要略高于本文方法，不过，本文方法的点对已经够密集了，重要的是其分布情况要优于ASIFT算法（见图6中用椭圆圈出的6个局部对比区域）。

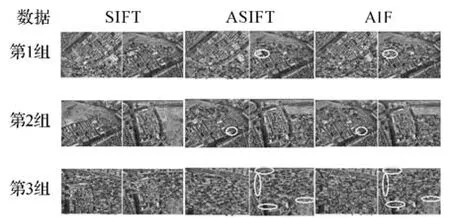
图6 3种方法分别对3组数据的匹配效果Fig.6 The matching result of three algorithms

表3 3种方法分别对3组数据的匹配总数和匹配准确率Tab.3 The experimental result of three algorithms

试验结果表明，本文算法比ASIFT算法具有更强的抗视点变化能力，其主要原因是：①通过影像粗略的角元素计算出的相机轴定向参数比ASIFT粗略模拟的相机轴定向参数要准确；②本文的匹配策略要优于ASIFT算法的匹配策略（由于ASIFT提取的特征点数量庞大，为了得到正确率高的匹配点对，其采用了极其严格的匹配策略：比值提纯法，阀值0.36），而SIFT在某些情况下，不具备抗视点变化能力。

4.2 AIF算法的计算复杂度

若平面上任意区域D，经仿射变换（D′＝Aft×D，仿射矩阵为A）后为D′，则两区域面积之比为，即。本文中通过对原始影像作逆仿射变换得到纠正影像仿射矩阵为A－1），所以，纠正影像（有纹理区域）的面积S′与原始影像面积S之间应满足如下关系：而故其中θ为倾斜影像的倾角。

ASIFT算法需要用61次来粗略模拟相机轴定向参数，通过仿射变换得到一组图像序列（共61张影像），其总面积约为原始影像的13.5倍［11，16］。AIF算法先通过估算影像的旋转矩阵直接计算出相机轴定向参数，再通过1次逆仿射变换得到1张纠正影像，其面积约为原始影像的cosθ倍。

由于图像局部特征的计算量与输入图像面积基本成比例［5］，对于下视影像与侧视影像的匹配：AIF算法用于SIFT特征提取和描述的影像面积约为原始影像的倍（由于各视影像大小几乎相等，看作等大），即AIF在特征提取阶段的时间复杂度约为SIFT算法的0.85倍，而ASIFT在特征提取阶段的时间复杂度约为SIFT算法的13.5倍。AIF算法在匹配阶段的时间复杂度约为SIFT算法的倍，而 ASIFT算法在匹配阶段的时间复杂度约为SIFT算法的倍。对于侧视影像与侧视影像的匹配：AIF用于SIFT特征提取和描述的影像面积约为原始影像的71倍，即AIF在特征提取阶段的时间复杂度约为SIFT的0.71倍，而ASIFT在特征提取阶段的时间复杂度约为SIFT的13.5倍。AIF在匹配阶段的时间复杂度约为SIFT的0.50倍，而ASIFT在匹配阶段的时间复杂度约为SIFT的倍。因此，AIF算法在特征检测和匹配阶段的计算复杂度要远低于ASIFT算法，且低于SIFT算法。3种匹配算法的匹配耗时，如表4。

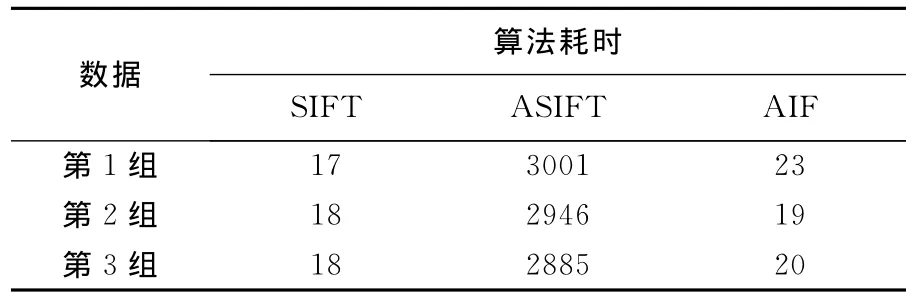
表4 3种方法的效率对比Tab.4 The time cost of three algorithms s

由表4可知，对于3组数据，AIF算法匹配耗时分别为 ASIFT算法的0.77%、0.64%、0.69%倍，分别为SIFT算法的1.35、1.06、1.11倍。结果表明，AIF算法的匹配效率要远远高于ASIFT算法，但比SIFT算法的匹配效率略低，其主要原因是由于本文算法的匹配策略要比SIFT算法的匹配策略复杂且计算量大。

5 结 论

本文针对ASIFT算法计算复杂度高的问题，提出了一种较为快速的倾斜影像匹配方法，该方法先恢复倾斜影像出现的仿射变形问题，再对纠正影像利用SIFT算法和一定的匹配策略进行匹配，最后将匹配出来的同名点对反算到原始影像上。下一步的研究重点是：①融合多种互补不变特征，有效保证匹配点对的多量性和空间分布均匀性［8，24］，设计一种重现率高、抗视点变化能力强、且具有尺度和旋转不变性的角点［3］；②优化算法的匹配策略，探索在由F、H矩阵引导的局部范围内进行匹配（在同名点的局部潜在范围内找到满足比值提纯法、NCC测度、主方向差异一致性的匹配点），使得匹配点对在重叠区分布更均匀、密集，并进一步减少误匹配率；③进一步增强匹配点对的可靠性，例如，在本文方法基础上，进行物方验证以增加匹配的稳定可靠性。在完成上述工作后，将该成果推广应用于倾斜影像空三软件和具体的项目实践中。

［1］MATAS J，CHUM O，URBAN M，et al.Robust Wide－baseline Stereo from Maximally Stable Extremal Regions［J］.Image and Vision Computing，2004，22（10）：761－767.

［2］MIKOLAJCZYK K，SCHMID C.An Affine Invariant Interest Point Detector［C］∥Proceedings of the 7th European Conference on Computer Vision（ECCV）.Copenhagen：Springer，2002：128－142.

［3］MIKOLAJCZYK K，SCHMID C.Scale ＆ Affine Invariant Interest Point Detectors［J］.International Journal of Computer Vision，2004，60（1）：63－86.

［4］MIKOLAJCZYK K，TUYTELAARS T，SCHMID C，et al.A Comparison of Affine Region Detectors［J］.International Journal of Computer Vision，2005，65（1－2）：43－72.

［5］MOREL J M，YU G S.ASIFT：A New Framework for Fully Affine Invariant Image Comparison［J］.SIAM Journal on Imaging Sciences，2009，2（2）：438－469.

［6］LOWE D G.Distinctive Image Features from Scale－invariant Key Points［J］.International Journal of Computer Vision，2004，60（2）：91－110.

［7］RICHARD H，ANDREW Z.Multiple View Geometry in Computer Vision［M］.2nd ed.United Kingdom：Cambridge University Press，2003：117－123.

［8］YANG H C，ZHANG S B，WANG Y B.Robust and Precise Registration of Oblique Images Based on Scale－invariant Feature Transformation Algorithm［J］.IEEE Geoscience and Remote Sensing Letters，2012，9（4）：783－787.

［9］WANG C Y，ZHANG Y，WU Y，et al.Highly Accurate Geometric Correction for Serious Oblique Aero Remote Sensing Image Based on the Piecewise Polynomial Model［J］.Journal of Computational Information Systems，2011，7（2）：342－349.

［10］YU Y N，HUANG K Q，CHEN W，et al.A Novel Algorithm for View and Illumination Invariant Image Matching［J］.IEEE Transaction on Image Processing，2012，21（1）：229－240.

［11］YU G，MOREL J M.ASIFT：An Algorithm for Fully Affine Invariant Comparison［J/OL］.Image Processing On Line，2011.［2013－11－29］.http：∥dx.doi.org/10.5201/ipol.2011.my－asift.

［12］YU G，MOREL J M.A Fully Affine Invariant Image Comparison Method［C］∥Proceedings of IEEE International Conference on Acoustics，Speech and Signal Processing.Taipei：IEEE，2009：1597－1600.

［13］OJI R.An Automatic Algorithm for Object Recognition and Detection Based on ASIFT Key Points［J］.Signal ＆Image Processing：An International Journal，2012，3（5）：29－39.

［14］ISHII J，SAKAI S，ITO K，et al.Wide－baseline Stereo Matching Using ASIFT and POC［C］∥Proceedings of 19th IEEE 2012International Conference on Image Processing.Orlando，Florida：IEEE，2012：2977－2980.

［15］ANCUKIEWICZ D，SIDERIS K，RICKETT A.3D Reconstruction from RGB and Depth Video［EB/OL］.［2014－01－10］.http：∥cs.ucla.edu/～costas/kinect＿reconstruction.html.

［16］OHTA M，IWAMOTO K，SATO Y，et al.Perspective Robust Object Identification Using Depth and Color Image Sensor for Real－world Annotation［C/OL］∥ The 5th International Conference on 3DSystems and Applications，2013.http：∥ www.3dsa.kr/3DSA2013/contents/program.html.

［17］ZHANG Li，GRUEN A.Multi－image Matching for DSM Generation from IKONOS Imagery［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2006，60（3）：195－211.

［18］ZHANG Li，ZHANG Jixian.Multi－image Matching for DEM Generation from Satellite Imagery［J］.Science of Surveying and Mapping，2008，33（Suppl）：35－39.（张力，张继贤.基于多基线影像匹配的高分辨率遥感影像DEM 自动生成［J］.测绘科学，2008，33（专刊）：35－39.）

［19］BON A D.Initial Approximations for the Three－dimensional Conformal Coordinate Transform［J］.Photogrammetric Engineering ＆ Remote Sensing，1996，62（1）：79－83.

［20］KLIPPENSTEIN J，ZHANG H.Quantitative Evaluation of Feature Extractors for Visual SLAM［C］∥Proceedings of the 4th Canadian Conference on Computer and Robot Vision.Quebec：IEEE，2007：157－164.

［21］LEŠKOVSKY′P，ALEKSEYCHUK A，STANSKI A，et al.Point－based Registration of High－resolution Histological Slices for Navigation Purposes in Virtual Microscopy［J］.Annals of the BMVA，2012，2012（10）：1－18.

［22］MIKOLAJCZYK K，SCHMID C.A Performance Evaluation of Local Descriptors［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（10）：1615－1630.

［23］LEI Lin，CHEN Tao，LI Zhiyong，et al.A New Approach to Image Invariant Extraction under Global Affine Transformation［J］.Journal of National University of Defense Technology，2008，30（4）：64－70.（雷琳，陈涛，李智勇，等.全局仿射变换条件下图像不变量提取新方法［J］.国防科技大学学报，2008，30（4）：64－70.）

［24］YAO Guobiao，DENG Kazhong，ZHANG Li，et al.An Automated Registration Method with High Accuracy for Oblique Stereo Images Based on Complementary Affine Invariant Features［J］.Acta Geodaetica et Cartographica Sinica，2013，42（6）：869－876，883.（姚国标，邓喀中，张力，等.融合互补仿射不变特征的倾斜立体影像高精度自动配准方法［J］.测绘学报，2013，42（6）：869－876，883.）