关于分数阶导数定义的商榷

吴 佳 施伟辰

(上海海事大学物流工程学院，中国 上海201306)

0 引言

分数阶微积分[1-3]的研究历史很久远，要上溯到17世纪。1695年，在L’Hospital在给Leibniz的著名信中提到了关于某一函数的n阶导数，当n为二分之一时，结果会是如何，从而产生了分数阶微积分。对于分数阶微积分的研究， 首先是在数学上，Euler、Laplace、Abel、Fourier、Liouvile 对分数阶微积分的研究做了一些工作。但是，第一本关于分数阶微积分理论的专著[4]直到 1974 年才出版。 随着 Caputo、Riemann、Grünwald、Hadamard、Letnikov、Hardy、Riesz、Marchaud、Littlewood、Ross等数学家或物理家对分数阶微积分的贡献，形成了现在被公认的几种分数阶导数的“定义”，其中包括 Riemann-Liouville“定义”和 Caputo“定义”[5]。

在最近几十年间，对于分数阶微积分应用的研究有了较大的发展，在科学及工程中的很多领域都有重要的应用，这些领域包括生物材料[6-7]，控制和机器人[8-9]，粘弹性动力学[10-11]，量子力学[12-13]等等。 在这些众多涉及到分数阶导数理论应用的文献中，都是直接引用上述“定义”的说法。

本文经仔细回顾R-L和Caputo的所谓“定义”，发现它们都是源自于分数阶导数（0＜α＜ 1 ）而得到的两个不同的表达式，含义相同并且互为等价。因此，我们认为，分数阶导数的定义仍然为（0＜α＜ 1 ）。 而RL和Caputo或者其他的所谓“定义”应称作R-L和Caputo等的分数阶导数的计算公式。

1 数学归纳法推导分数阶导数的计算公式

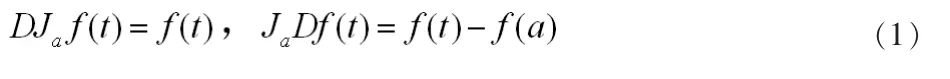
对任何自然数n有

对连续函数f（t），反复应用分部积分法可得

当 n＝2 时，有

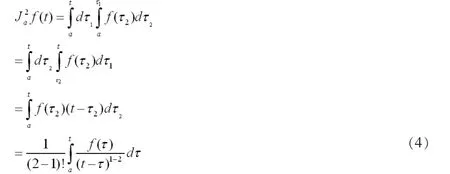
假设 n=k-1 时式（3）成立，则

从而当时，

因此式（7）成立。

对于非正整数的正数a＞0，记[a]为不超过a的最大整数，取m＝[a]+1。令

显然，由式（8）我们知道式（9）和式（10）是等价的，他们只是表达形式不同，含义相同。 所以，分数阶导数的定义应该是（0＜α＜ 1 ），而式（9）和式（10）只是两种不同的计算表达式。把式（9）和式（10）称作“定义”并不妥当，而把它们称作计算公式更为贴切。

由此可见，或许可能还有很多其他所谓的分数阶导数的“定义”，但如果都是源自于式，他们也只是不同的计算公式，而非定义。

由于R-L和Caputo的所谓 “定义”都是是等价的源于（0＜α＜ 1 ），所以被称作“定义”并不妥当。 分数阶导数的定义是（0＜α＜ ）1 ，而R-L和Caputo的所谓“定义”应该改称为R-L和Caputo的分数阶导数的计算公式。

［1］S.G.Samko,A.A.Kilbas and O.I.Marichev,Fractional Integrals and Derivatives：Theory andApplications[M].Gordon and Breach,New York,1993.

［2］I.Podlubny,Fractional Differential Equations[M].Academic Press,San Diego,1999.

［3］A.A.Kilbas，H.M.Srivastava and J.J.Trujillo,Theory and Applicationsof Fractional DifferentialEquations[M].Elsevier,Amsterdam,2006.

［4］Oldham K B,Spanier J.The Fractional Calculus [M].New York-London:Academic Press,1974.

［5］Li Xiao-rang.Fractional Calculus,Fractal Geometry and Stochastic Process[D].Ontario:The University of Western Ontario USA,2003.

［6］W.G.Gl?ckle and T.F.Nonnenmacher,A fractional calculus approach to selfsimilar proteindynamics[J].Biophysical Journal,1995,68:46-53.

［7］M.Kopfet al，Anomalous diffusion behavior of water in biological tissues[J].BiophysicalJournal,1996.

［8］]R.R.Nigrnatullin and S.I.Osokin,Signal processing and recognition oftree kinetic equationscontaining non—integer derivatives from law dielectric data[J].Signal Processing，2003，83:2433-2453.

［9］M.D.Ortigueira,On the initial conditions incontinuous-time fractional linear systems[J].Signal Processing,2003.

［10］R.Metzler and T.F.Nonnenmacher,Fractional relaxation processes and fractional rheologicalmodels for the description of a class of viscoelastic materials[J].Int.J.Plasticity,2003.

［11］A.Chatterjee,Statistical origins offractional derivatives in viscoelasticity[J].Journal ofSoundand Vibration,2005,284：1240-1245.

［12］N.Laskin,Fractional quantum mechanics and Lévy path integrals[J].Phys.1ett.A 268(2000)：297-305.

［13］D.Baleanu and S.I.Muslih,About fractional supersymmetric quantum mechanics[J].Czechoslovak Journal of Physics,2005,55(9):1062-1066.