气力输送管道固有频率及共振分析

孙丹凤，马咏梅，冯成德，孙四中

(四川大学制造科学与工程学院,四川 成都 610065)

DOI:10.3969/j.issn.2095-509X.2015.10.002

气力输送管道固有频率及共振分析

孙丹凤，马咏梅，冯成德，孙四中

(四川大学制造科学与工程学院,四川 成都 610065)

利用气力输送管道输送颗粒状物质，根据输送颗粒量及时间设计出管道结构。利用经验公式得到气柱固有频率及激振频率，用ANSYS Workbench进行模态分析和理论计算,得到管道的固有频率以及流固耦合对管道固有频率的影响。结果表明，流固耦合作用下，管道固有频率稍有增大；当管道长度在某一范围内时，管道固有频率、气柱固有频率或激振源频率处于共振区。研究结果为管道振动分析与管道结构设计提供了理论依据。

气力输送；固有频率；流固耦合；管道振动

气力输送是利用具有一定压力和气流速度的气体输送颗粒状物料的输送方法[1]，在颗粒状物质输送中有着广泛的应用。在气力输送过程中，由动力源产生的管流脉动会引起管道振动，管道振动会造成颗粒的破损以及管道本身的破坏。当管道系统的固有频率、管道内运送颗粒的气柱固有频率及激振频率任意两者之间相等或接近时将导致共振，使管道振动幅度增大，振动噪声增强，严重时将损坏管道。大量学者对管道振动问题进行了研究。龚善初[2]应用振动分析法研究气体管道的振动，对振动原因进行了具体分析,提出了相应的消振措施。苏欣平等[3]对管道振动机理进行了分析，运用弹性力学理论，建立了管道系统振动的数学模型。陈贵清等[4]针对某压力管道结构，采用两端简支梁模型，进行了流固耦合的振动计算，探讨了物理参数对固有频率的影响。

本文利用数学计算及仿真分析方法求出了管道系统的固有频率、气柱的固有频率及激振频率，探究了管道发生共振的原因，为管道的结构设计与优化提供了理论依据。

1 管道初步设计

1.1 输送颗粒参数的选择

根据输送颗粒的质量和输送时间初步设计管道，确定气力输送中浓度比、输送风速、输送量等参数。

1)浓度比。

粮食输送为稀相输送，浓度比的计算式为[1]：

式中：G物为单位时间内输送颗粒质量，kg/s；ρ气为输送管内单位体积的空气质量，kg/m3；Q时为单位时间内消耗空气的体积，m3/s。

2)输送风速。

在稀相输送中，输送风速v在12～40m/s之间，本文取v=20m/s。

3)输送量。

根据输送总量和时间的要求[5]，确定单位时间内的输送颗粒容积量Q为2.26×10-3m3/s。

1.2 管道参数选择

1)管径选择。

由式(2)[1]计算可得管道内径d为200mm。

式中：v介为颗粒介质的平均流速。

2)管道材料的选择。

根据输送介质选择管道材料。对于稀相气力输送，物料在输送管道中呈悬浮状态，颗粒与管道内壁的碰撞造成能量的损失，不同的管道材料，其黏附性能和摩擦系数差异较大，相应的输送能耗差别也较大。本文所选管道材料为Q235碳钢，其弹性模量E为200GPa ，泊松比为0.3。

3)管道壁厚的选择。

通过查文献[6]，选择管道的内径d为200mm，外径D为219mm。

2 固有频率计算

2.1 气柱固有频率

在稀相输送中，气体体积占管道内输送介质的比例很大，气柱对管道振动的影响较大，其固有频率可根据式(3)[2]计算：

式中：i为气体固有频率阶次；a为声音在气体中的传播速度(本文中利用空气输送粮食，且为稀相输送，所以a为声音在空气中的传播速度340m/s)；L为管道长度，m。

2.2 激振频率计算

在此次设计中输送动力为复式压缩机，型号为ZTY265，压缩机每转动一周，向管道吸气排气各2次，即m=2 ，曲轴转速n=400r/min，则激振频率[7]F激=mn/60=13.30Hz。与激振频率处于共振区的频率F共振=(0.8～1.2)F激，为10.67～16.00Hz。

2.3 管道结构固有频率计算

2.3.1 ANSYS Workbench 仿真分析

在ANSYS Workbench的Modal模块中设置材料属性。建立管道模型如图1所示。网格单元尺寸设置为10mm,选择自动划分方式划分网格。管道采用两端固定的支承方式，添加两端固定约束。利用ANSYS Workbench对管道进行模态分析[8]，得到管道结构前六阶振动频率如图2所示，一阶、二阶固有频率振型如图3所示。

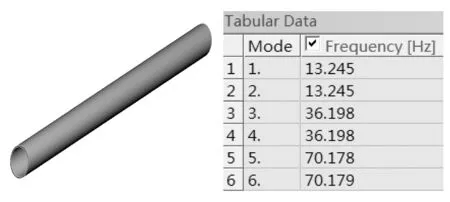
图1 管道结构模型 图2 管道结构前六阶固有频率

2.3.2 理论计算

直管两端支承方式为固支，其均布质量看作为中间等效集中质量，其固有频率计算公式[9]为：

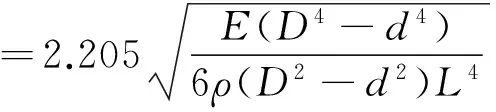
(4)

图3 管道一、二阶固有频率振型

式中：ρ为管道密度，kg/m3。

管道固有频率计算值与仿真结果比较见表1。

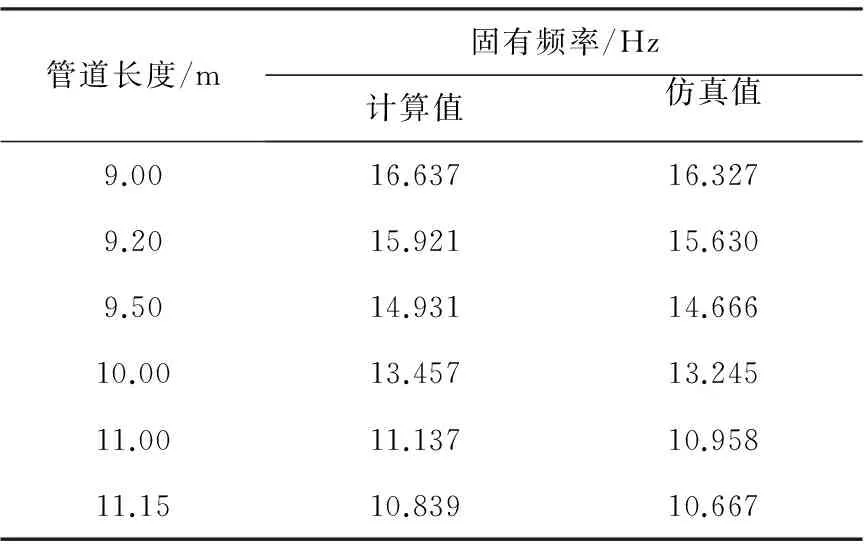
表1 管道固有频率计算值与仿真结果比较表

由表1可知，管道固有频率的计算值与模态仿真分析值相差很小，验证了仿真分析的正确性。模态仿真分析可得出管道振型，为减振及与流固耦合分析比较提供了基础。在设计管道时，可运用仿真和理论计算两种方法。

2.3.3 流固耦合分析

在气力输送管道中，管道内的流体会对管道结构的固有频率产生影响，需对管道进行流固耦合模态分析。在ANSYS Workbench中进行单向流固耦合模态分析[10]。首先在流体模块CFX中进行流体分析，将流体分析结果导入static structural中，作为结构场分析的初始条件，求解出管道预应力，在模态分析模块中求解出管道的前六阶模态大小。

1)流体分析。

在CFX中建立长度为10 000mm、直径为200mm的流体模型，选择Automatic Method划分网格，流固耦合面上流体网格大小与固体结构网格大小保持一致；建立流体域模型，将流体简化为气体，气体绝对压强由式(5)、(6)计算得出，为0.997 6MPa；进口速度设置为20m/s ，出口压力设置为大气压0.1MPa；在CFX-solver Manager中进行求解。

气体绝对压强计算式为：

式中：r为流体的密度重度，kg/m3；v0为气体流速，m/s。

式中：Pt为气体对管道壁的绝对压强；P0为大气压。

在流体分析模块得到的流体动态特性收敛情况如图4所示。

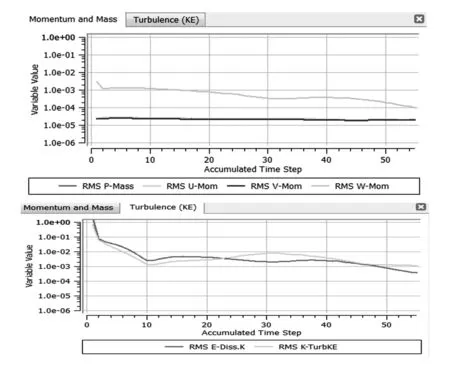
图4 流体动态特性收敛情况

2)结构模态分析。

除添加流场压力载荷外，其他设置和管道模态分析设置相同。添加流场压力载荷后管道应力图如图5所示。

图5 添加流场压力载荷后管道应力图

计算出管道预应力，将结果导入ANSYS Workbench的模态分析模块中，得到流固耦合下管道结构前六阶固有频率。其中第一阶、第二阶振型如图6所示。流固耦合后管道固有频率与空管结构固有频率的比较见表2。

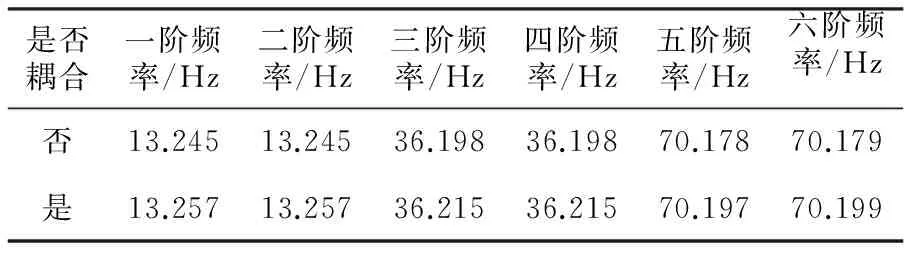
表2 是否进行流固耦合管道固有频率比较

图6 流固耦合下管道一、二阶固有频率振型

由表2可知，在气力输送管道中，流固耦合后所得管道结构固有频率相对于空管固有频率略微增大。

3 共振分析

3.1 气柱与激振源共振分析

当F气柱=(0.8～1.2)F激时，气柱与激振源处于共振区，共振长度L共振=(0.8～1.2)ia/4F激。当i=1时，L共振=5.11～7.67m；当i=2时，L共振=10.22～15.34m。在设计管道时要避免管道直管长度处于此范围内。

3.2 管道与气柱共振分析

管道结构固有频率与气柱固有频率相等或接近时，即式(7)成立，则管道与气柱处于共振区。

计算所得气柱一、二阶固有频率与管道一阶固有频率如图7所示。

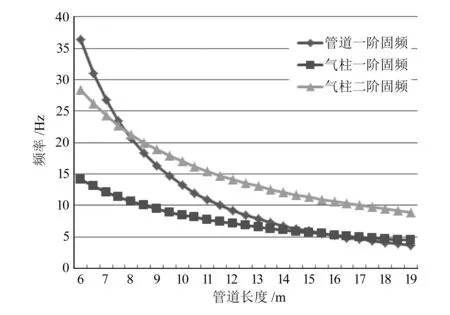
图7 不同管道长度下管道与气柱固有频率值

由仿真分析与计算结果可以看出，在管道长度为6.5～10.0m时，管道固有频率与气柱二阶固有频率接近或相等，处于共振区；在管道长度为13.0～19.5m时，管道固有频率与气柱一阶固有频率相等或接近，处于共振区。

3.3 管道与激振源共振分析

管道固有频率和激振源频率相等或接近时，即式(8)成立，此时管道与激振源处于共振区。

F管=(0.8～1.2)F激

(8)

利用仿真分析得到管道固有频率，不同长度管道的一阶固有频率如图8所示。

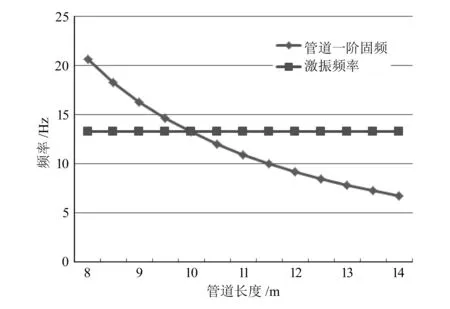
图8 不同管道长度下管道一阶固有频率

由图8 可得，管道固有频率随管道长度的增大而减小，当管道长度在9.0～11.0m时，管道固有频率接近激振频率13.30Hz，管道和激振源就会发生共振，因此在设计管道时要注意管道长度，避免管道发生共振。

4 结论

本文根据输送颗粒质量与时间对管道结构进行了初步设计，并运用模态仿真和理论计算对管道进行分析，得到以下结论：

1)通过流固耦合模态分析可知，管道结构固有频率比空管结构固有频率稍有增大。

2)采用ANSYS Workbench模态分析和理论计算可知，管道结构的固有频率随管道长度增大而减小，在长度达到某个范围时,管道固有频率与激振源频率或气柱固有频率接近或相等,因此会产生共振。

本文的研究内容对气力输送管道的设计及避免管道共振有一定的指导作用。

[1] 颜海霞.气力输送系统中出料阀内气固两相流动的研究[D].杭州：浙江大学，2005.

[2] 龚善初.气体管道振动分析与消振措施[J].煤炭技术,2004，23(9)：97-99.

[3] 苏欣平，闫祥安，张承谱.管道结构振动有限元分析及减振研究[J].工程设计学报，2002,9(3):141-143.

[4] 陈贵清，郝婷，戚振宕.物理参数对压力管道振动固有频率的影响[J].唐山学院学报，2005，18(4):96-99.

[5] 蒋克敏.大豆气力输送的设计和应用[J].油脂科技，1984,(增1):103-108.

[6] 《冶金工艺管道设计手册》编写组.湿法冶金工艺管道设计手册[M].北京：原子能出版社,1981.

[7] 樊长博,张来斌,王朝晖,等.往复式压缩机气体管道振动分析及消振方法[J].科学技术与工程,2007,7(7):1309-1313.

[8] 高耀东,宿福存. ANSYS Workbench机械工程应用精华30例[M]. 北京：电子工业出版社,2013.

[9] 《化工厂机械手册》编辑委员会.化工厂机械手册： 管路维修、设备管理[M].北京：化学工业出版社,1989.

[10] 宋学官.ANSYS流固耦合分析与工程实例[M].北京：中国水利水电出版社,2012.

Analysis on the natural frequency and resonance vibration for pneumatic conveying pipeline

SUN Danfeng, MA Yongmei, FENG Chengde, SUN Sizhong

(School of Manufacturing Science and Engineering, Sichuan University, Sichuan Chengdu, 610065, China)

Pneumatic conveying pipeline is used to convey granular material,and the pipeline structure is designed according to the quantity of particles and time. Empirical formulas are used to get the gas column natural frequency and excitation frequency. It uses modal analysis ANSYS Workbench and theoretical calculation to calculate the natural frequency of the pipe and the fluid-structure interaction effect on the natural frequency of the pipeline structure. The results show that under the action of fluid-structure interaction, natural frequency of the pipe increases slightly, when the pipe length reaches a certain scope, pipelines, gas column or excitation source are in the resonance region. This provides a theoretical basis for the pipeline vibration analysis and structural design of the pipeline.

pneumatic conveying; natural frequency; fluid-solid coupling resonance; pipeline vibration

2015-08-03

四川省科技支撑计划项目(2013GZX0159-3)

孙丹凤(1989—)，女，河南商丘人，四川大学硕士研究生，主要研究方向为机械结构设计和减振。

TH122

A

2095-509X(2015)10-0007-04