风力发电机组恒功率无模型自适应变桨距控制

姜 萍 赵振家

(河北大学 a. 电子信息工程学院；b. 罗克韦尔自动化实验室，河北 保定 071000)

我国始终把可持续发展作为基本战略路线，随着近年煤炭及石油等常规能源的全面紧张，可再生能源的发展已是大势所趋。我国风能资源丰富、且其成本相比其他可再生能源较低，在可再生能源中最具商业化和产业化发展前景。

近几年来，变桨距风力发电机逐渐代替定桨距风力发电机成为主流机型。当风速达到额定风速以上时，变桨距风力发电机组可通过改变桨距角实现弃风，保持额定功率，实现功率的稳定。现如今大部分变桨距风力发电机组都采用PID算法，该算法简单、易实现，但对于风力发电机组非线性、强耦合的特性，无法更好地维持功率恒定，因此如何改进算法，改善风力发电机组的控制性能，成为研究变桨距风力发电机的热点之一。

罗秋滨等分析了无模型控制的抗干扰能力，克服了PID控制无法对非线性、强耦合系统实现稳定控制的弱点，并通过与PID调节器的抗干扰能力的仿真比较，进一步说明了无模型控制方法具有很强的抗干扰能力，对多变量强耦合系统进行控制可收到良好的效果[1～3]。曹荣敏和侯忠生利用Matlab软件进行仿真实验，证明了无模型方法对电机这种具有不确知动态非线性系统的有效性和稳定性[4]。金尚泰等将无模型自适应控制算法应用到永磁直线电机的速度控制中，控制器的设计仅需系统的输入、输出数据，并能够实现参数适应性控制和结构自适应控制，仿真结果验证了无模型自适应算法的有效性[5]。秦生升等基于微分几何反馈线性化方法，提出变桨距风力发电机组恒功率控制策略，并将精确反馈线性化与H∞控制理论相结合设计了非线性H∞控制器，将其运用在风电变桨距控制中，在风速高于额定风速时调节风力机维持额定转速[6，7]。张纯明等根据模型参考自适应控制原理，以大型风力发电机组直流电动变桨距控制系统为研究对象，设计了一个高性能电动变桨距控制系统，并用李雅普诺夫稳定性分析给出自适应系统控制律[8]，仿真表明所设计系统有很好的跟踪和伺服性。笔者基于无模型理论，设计了无模型自适应控制器，并将其运用在风电系统的变桨距控制中。

1 风力发电机组模型①

风力发电系统主要由风力机、齿轮传动和发电机构成，其运行特性和控制策略与所用发电机类型和风力机特性密切相关。当风速从接近零上升到切入风速时，风力机经过齿轮传动带动发电机进行发电。根据不同的风况，风力发电系统的运行可以分为启动区、最大风能追踪区、恒转速区和恒功率区[9]。

1.1 风力机模型

风轮是一种能截获流动空气所具有的动能，并将风轮叶片迎风扫掠面积内的一部分动能转化为有用机械能的装置圈。

由空气动力模型可知，风力机吸收的机械功率为：

(1)

风力机的运动方程为：

(2)

风力机转矩与功率的关系为：

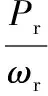
(3)

式中Cp(λ，β)——风能利用系数；

Jr——转动惯量；

Pr——风力机捕获的机械能；

R——风轮半径；

V——风速；

β——桨距角；

ρ——空气密度。

Cp(λ，β)的表达式为：

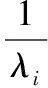
(4)

风轮所捕获的风能与风速是3次方的非线性关系，Cp(λ，β)又具有λ，β的非线性特性，风力机的转矩和功率之间又存在着某种耦合，因此风力机是一个非线性、强耦合的系统。

1.2 齿轮传动模型

根据风轮气动特性，风轮产生的转矩Tr作用在带有转动惯量Jg的风轮上。风轮通过增速比为n的增速器连接到转动惯量Jg的发电机上，发电机将产生反转矩Te，得到传动系统的质量块模型：

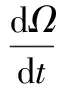
(5)

其中，k为常数。

1.3 异步电机模型

异步电机的运动方程为:

(6)

式中Jg——发电机的转动惯量；

Te——发电机上的反扭矩；

Tm——高速轴上的扭矩；

ωg——发电机的机械角速度。

异步电机的电磁转矩为[10]：

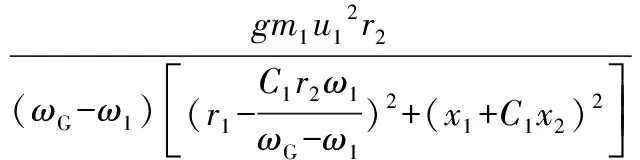
(7)

式中C1——修正系数；

g——发电机极对数；

m1——相数；

r1、r2——分别为定子和归算后转子绕组的电阻；

x1、x2——分别为定子和归算后转子绕组的漏抗；

u1——电网电压；

ω1——同步转速；

ωG——发电机的当量转速。

异步发电机的功率需要去除不确定的铜损耗和铁损耗，并且转矩又与电压、角速度存在非线性、强耦合关系，所以异步电机也是一个非线性、强耦合的系统。

综上，风力发电机组中存在大量非线性、强耦合环节，传统的PID调节已经不能满足生产实际的要求，因此需要寻找更优的控制策略以对非线性、强耦合系统实现更好的调节。

2 变桨距原理

风机上的桨距角指的是叶片顶端翼型弦线与旋转平面的夹角。调节桨距角的目的主要有：在启动时获得比较大的气动扭矩，使叶轮克服驱动系统的空载阻力矩；在额定风速后，限制功率输出，使功率平稳，保护机械和电路系统，同时降低载荷；刹车时，提供很大的气动阻力，使叶轮的转速快速降低，避免机械刹车造成惯性力太大而造成的伤害。

根据不同的风况，风力发电系统的运行可以分为启动区、最大风能追踪区、恒转速区和恒功率区。在启动区内，风速大于或等于切入风速时发电机并网发电；在最大风能捕获区风力机组并网运行在最高转速以下，风力机桨距角处于不调节的定桨运行状态；在恒转速区风力发电机组已达到最高转速，但风力机的输出功率尚未达到额定输出状态，为保护机组不过载，不再进行最大风能追踪运行，而是通过风力机子系统的变桨距控制来调节桨距角，确保在允许最大转速上的恒转速发电运行；在恒功率区，随着风速的增大风力机输出机械功率不断增大，发电机达到其功率上限。

2.1 风力发电机组功率和桨距角的关系

风力发电机组的功率和桨距角的关系可以近似表示为：

P(t+1)=f(P(t),P(t-1),…,P(t-ny),β(t),

β(t-1),…,β(t-nu))

(8)

2.2 控制律的计算

引入准则函数[11]：

J(β(k))=[|P*(k+1)-P(k+1)|2+

λ|β(k)-β(k-1)|2]

(9)

对β(k)求导并令其等于零，解得：

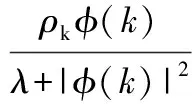
(10)

其中ρk是步长序列，λ是权重因子。控制律算法中λ的作用有两个：其一是限制了Δβ(k)的变化，因此可以间接限制伪偏导数值量的变化；其二是可避免控制律算法中分母可能出现为零的这种奇异情况。从控制律算法可以看出，此类控制律与受控系统数学的模型结构和系统阶数无关。

2.3 伪偏导数的计算

引入准则函数：

J(φ(k))=[(P*(k)-P(k-1)-φ(k)Δβ(k-1))2+

μ(φ(k)-φ(k-1))2]

(11)

进行与上述相类似的极小化程序，可以得到伪偏导数估计算法：

(12)

其中μ是权重因子，ηk是步长。

3 控制器的设计

由上述可以得到该系统不依赖于受控系统数学模型的无模型自适应方案[12]，即：

Δβ(k-1))

(13)

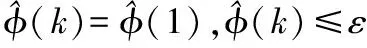
(14)

|Δβ(k-1)|≤ε

(15)

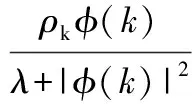
(16)

其中ηk，ρk∈(0，1]；μ，λ是权重因子；ε是一个充分小的数；φ(1)是φ(k)的初值。

笔者基于Matlab设计控制器，并将其在风力发电机组中进行仿真，当风速高于额定风速时，由实际功率和额定功率的偏差分别经过PID和无模型自适应(MFA)控制器进行调节。系统的结构框如图1所示。

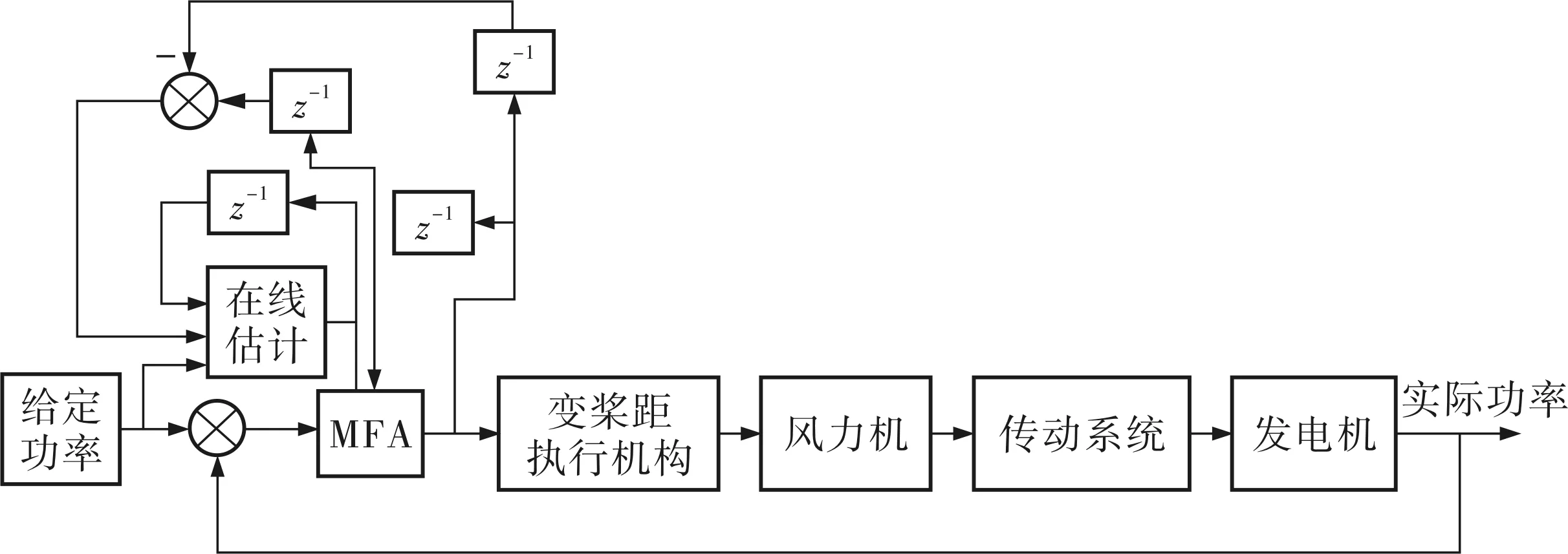
图1 无模型自适应变桨距原理框图

4 仿真分析

笔者基于Matlab/simulink对 3台3MW风力发电机组进行了仿真实验。定子的电阻为0.004 843(pu)，电感为0.124 8(pu)；转子的电阻为0.004 377(pu)，电感为0.179 11(pu)，互感为6.77(pu)，极对数为3，转动惯量为5.04(pu)，额定风速为9m/s。无模型控制器的参数λ=0.3，μ=0.8；PID控制器的参数kp=5，ki=25。当风速为阶跃风速时，所得发电机功率和风力机转速曲线如图2、3所示。

图2 阶跃风速下风力机功率效应曲线

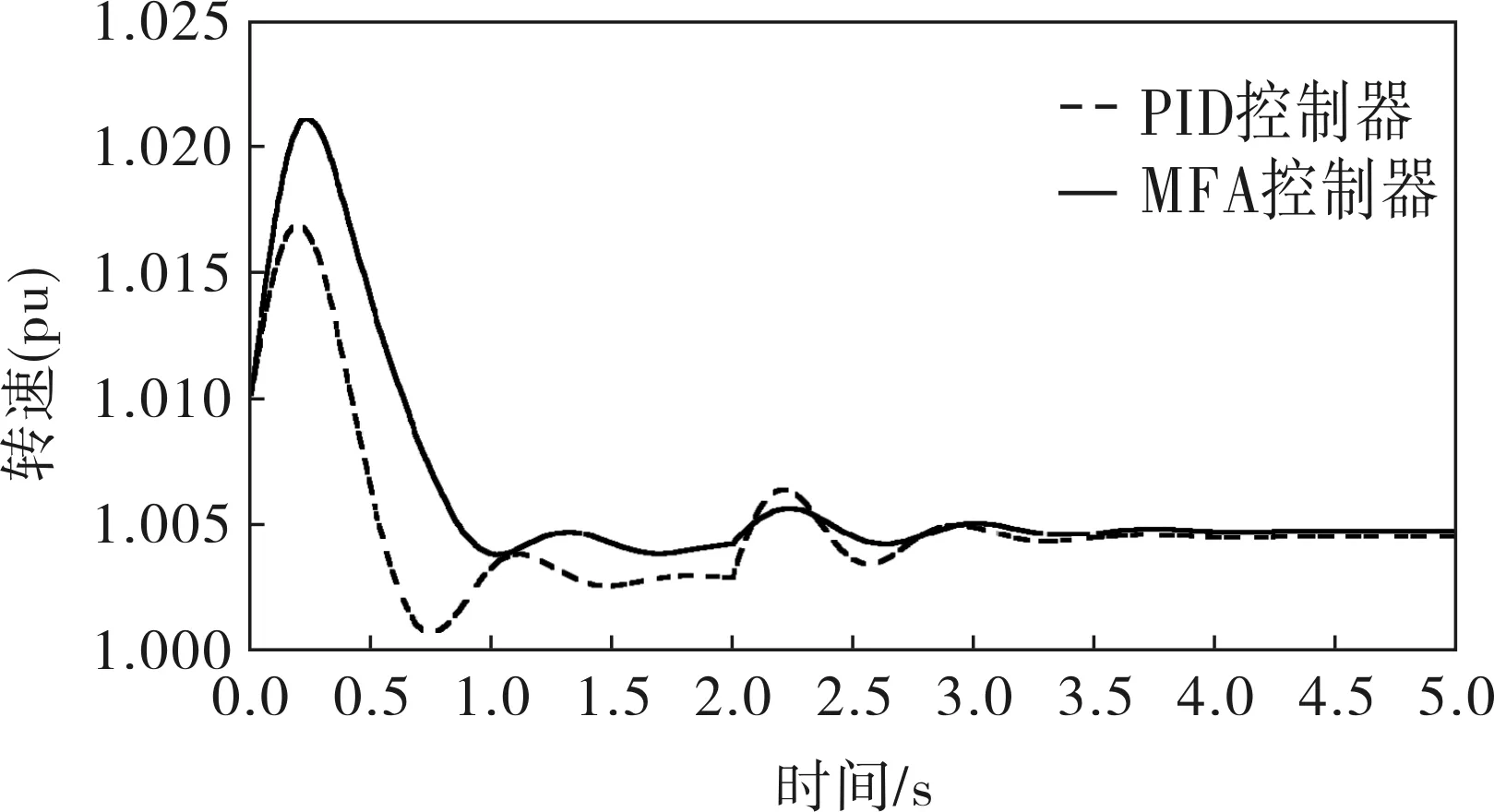
图3 阶跃风速下风力机角速度曲线

当风速为随机风速时，所得发电机功率和风力机转速曲线如4～6所示。

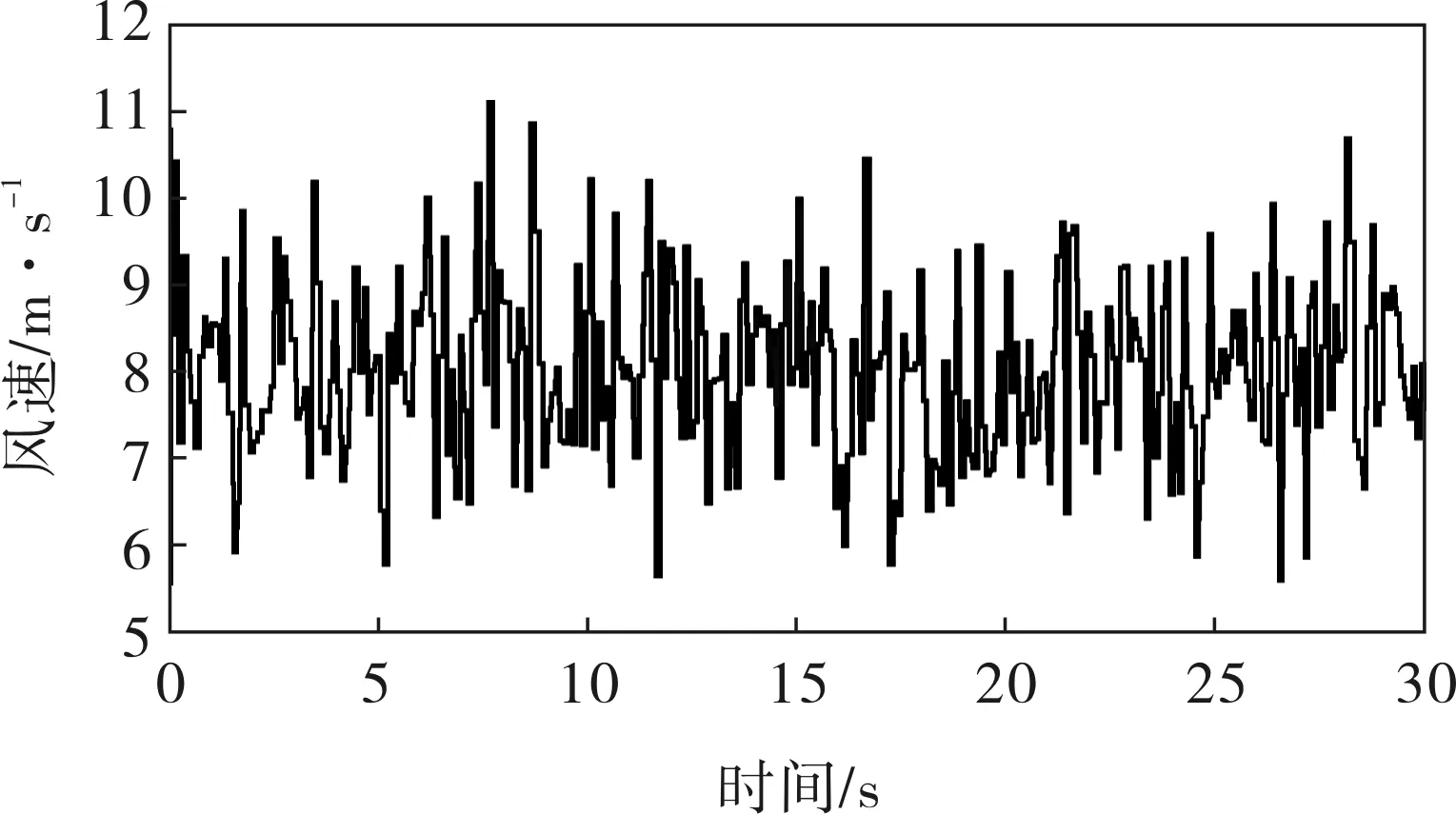
图4 随机风速实验曲线

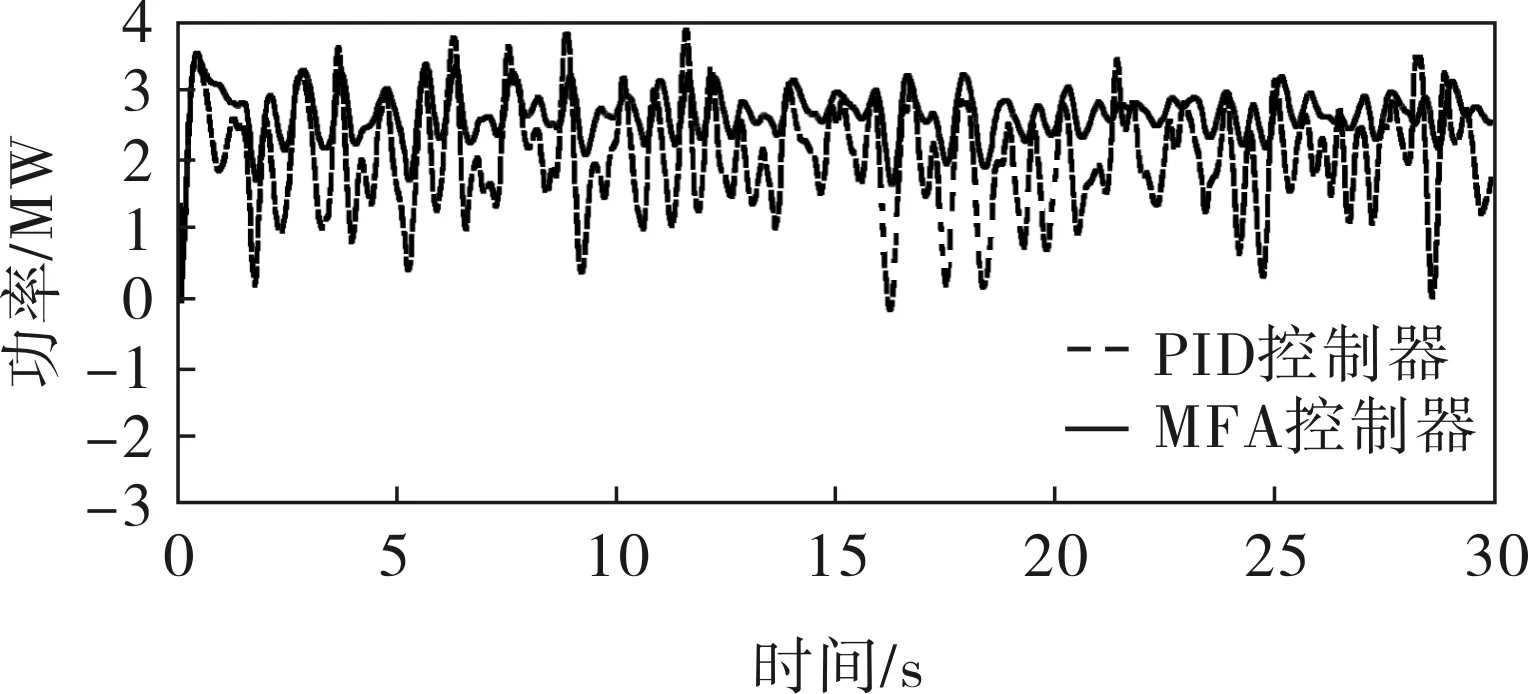
图5 随机风速下发电机功率曲线

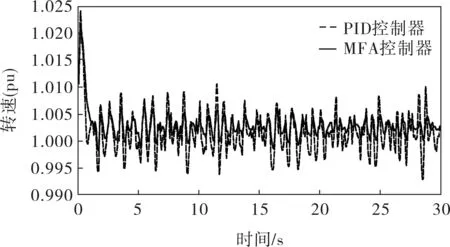
图6 随机风速下风力机角速度曲线

5 结束语

风力发电系统是一个非线性、强耦合的系统，并且风速的扰动性也极强。无模型自适应控制基于系统特性值动态估计，优化内部参数使系统克服时变和非线性，满足系统动态和稳态要求。从实验结果也可以看出，当风速在阶跃风速和随机风速下时，MFA控制器的控制效果明显要好于PID控制器的，能够更好地保持发电机的功率在额定功率下的稳定，实现恒功率控制。原因在于无模型自适应控制器能够适应于非线性、强耦合系统，并且其抗干扰能力要强于PID控制，因此无模型自适应控制要明显优于PID控制。

[1] 罗秋滨，李秀英，韩志刚.无模型控制方法的抗干扰能力分析[J].系统仿真学报，2008，20(13)：3472～3476.

[2] 蒋爱平，李秀英，韩志刚.从PID到无模型控制器[J].控制工程，2005，12(3)：217～221.

[3] 韩志刚，蒋爱平，汪国强.无模型控制方法对多变量耦合系统控制的应用研究[J].控制与决策，2004，19(10)：1155～1158.

[4] 曹荣敏，侯忠生.无模型控制方法在直线电机控制中的仿真研究[J].系统仿真学报，2006，18(10)：2874～2877.

[5] 金尚泰，侯忠生，王卫红.无模型自适应控制方法在永磁直线电机控制中的应用[C].Proceedings of the 26th Chinese Control Conference.Zhangjiajie：IEEE,2007：748～751.

[6] 秦生升，胡国文，顾春雷，等.风力发电系统的恒功率非线性H∞鲁棒控制[J].控制理论与应用，2012，29(5)： 617～622.

[7] 杨俊华，郑俭华，杨梦丽，等.变浆距风力发电机组恒功率反馈线性化控制[J].控制理论与应用，2012，29(10)： 1365～1370.

[8] 张纯明，姚兴佳，张忠丛，等.模型参考自适应电动变桨距控制[J].控制理论与应用，2008，25(1)：148～150.

[9] 贺益康，胡家兵，徐烈.并网双馈异步风力发电机运行控制[M].北京：中国电力出版社，2012.

[10] 王江.风力发电变桨距控制技术研究[D].合肥：合肥工业大学，2009.

[11] 侯忠生，韩志刚.非线性系统鲁棒无模型学习自适应控制[J].控制与决策，1995，10(2)：137～142.

[12] 韩志刚.无模型控制器的设计问题[J].控制工程，2002，9(3)：19～22.