正态云变论域模糊PID控制在循环流化床炉内脱硫系统中的应用

夏琳琳 文 磊 台金娟

(东北电力大学自动化工程学院，吉林 吉林 132012)

循环流化床锅炉是一种清洁燃煤锅炉，采用低温燃烧和循环燃烧技术，理论除硫效率高达90%[1]。炉内脱硫技术使脱硫过程不会腐蚀设备且成本合理，已广泛用于中小型电厂和旧电厂的改造[2]。但炉内脱硫系统具有大滞后、非线性、多参数的特性，当受负荷变化或干扰因素影响时，其对象特性参数或结构易发生改变。运用模糊数学去解决控制过程中各种信号量和评价指标的不易定量描述问题时，便可实现模糊自适应PID，处理过程涉及规则的条件、操作的模糊集表示、专家知识、模糊推理与决策[3]。

变量论域的可变思想是由我国学者李洪兴首次提出的，旨在保证规则形式不变的情况下，通过伸缩因子使论域随误差的变化而变化，提升系统的控制精度[4～7]。受上述思想的启发，笔者提出一种正态云的变论域模糊PID控制方法，利用云滴的确定度反映模糊性，借助自身概率意义下的随机性构成隶属云，取代模糊控制的隶属函数设计，实现定性概念与定量数值的不确定性转换。

循环流化床炉内脱硫是脱硫剂石灰石在炉膛煅烧分解生成CaO，CaO与原煤燃烧产生的SO2反应生成CaSO4,CaSO4进入灰渣中，以此达到脱硫的目的。影响循环流化床锅炉脱硫效率和SO2排放最主要的因素是Ca/S摩尔比，其直接反映了炉内石灰石的相对含量。参阅文献[8，9]，笔者最终选取某厂循环流化床机组在300MW(100%)、260MW(87%)、215MW(72%)和170MW(57%)4个负荷段的工况数据，以石灰石量阶跃扰动作为系统的输入，实际SO2浓度变化作为系统输出，通过曲线拟合，遵循较为合理的线性化假设，得到不同负荷工况下系统复域数学模型。

300MW(100%)负荷工况的数学模型：

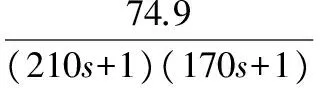
260MW(87%)负荷工况的数学模型：

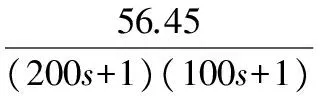
215MW(72%)负荷工况的数学模型：

170MW(57%)负荷工况的数学模型：

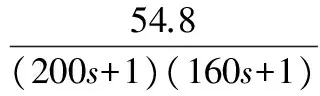
2 正态云变论域模糊PID控制器的设计与仿真

在模糊集和正态隶属函数概念上，李德毅等将概率论思想引入统计学中，刻画了正态云模型，即实现了模糊性(边界的亦此亦彼性)和随机性(发生的概率)的统一，证明了正态云的普适性[10 ，11],并分析了定性定量的不确定转换和产生条件[12]。

2.1 正态隶属云

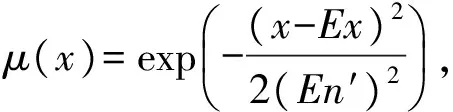
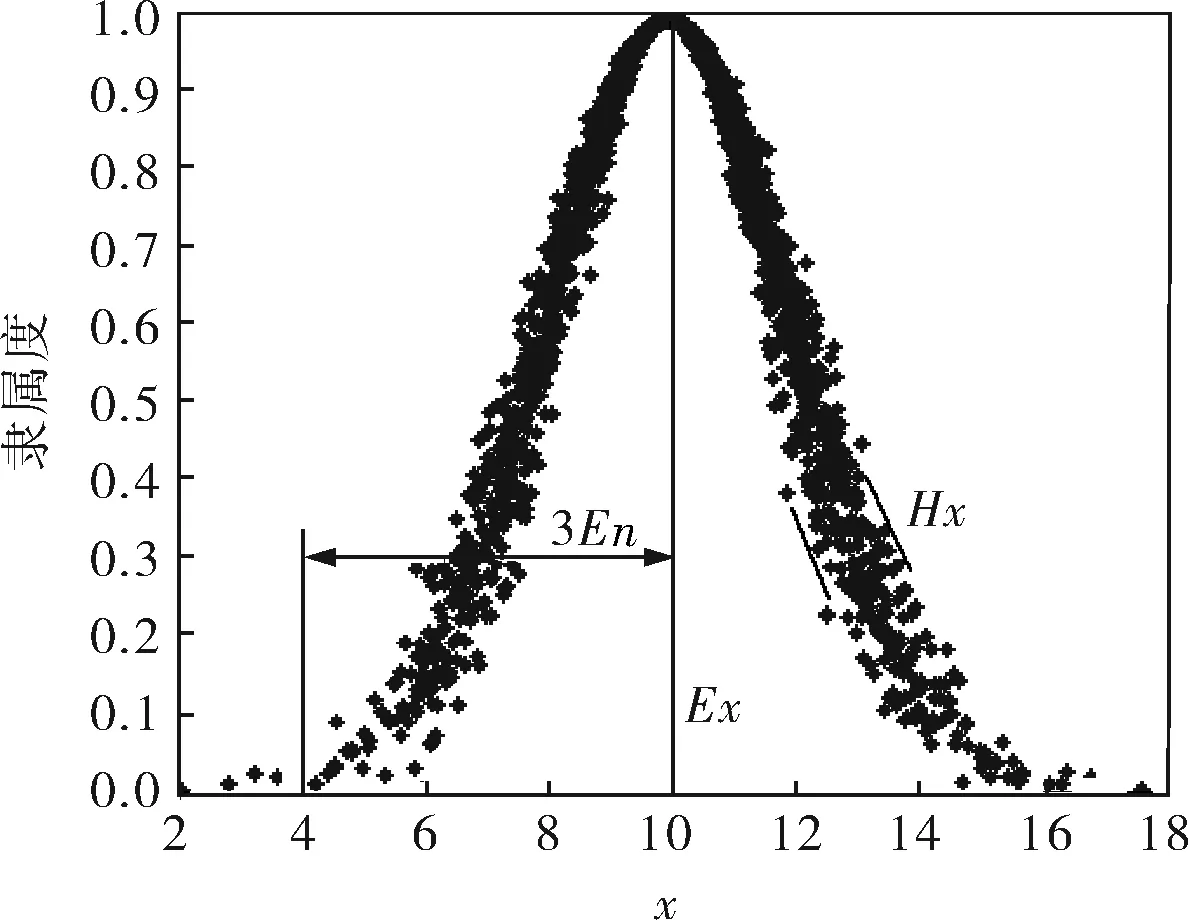
a. 一维云形态

b. 二维云形态

2.2 正态云变论域模糊PID控制

选取石灰石加入量的偏差e和偏差变化率ec为输入变量，其模糊语言变量分别为E和EC；以PID 3个参数的校正值Δkp、Δki、Δkd为输出变量，其模糊语言变量分别为Kp、Ki、Kd。 模糊输入/输出变量均以正大(PB)、正中(PM)、正小(PS)、零(O)、负小(NS)、负中(NM)、负大(NB)7个语言变量进行模糊子集划分。该多变量模糊控制器MVFC(Multiple Variable Fuzzy Controller)采用Mamdani型控制决策，IFE1 AndE2 THENH知识表示下变量间均含有49条控制规则(来自于操作人员或领域专家长期实践经验)，各模糊语句间采用“或”关系运算。限于篇幅，仅给出Δkp控制规则，见表1。

表1 Δkp控制规则

模糊控制器变论域的主旨思想是使输入/输出变量的基本论域随控制要求按一定准则在适当时刻做伸缩变化，使得定义在初始论域上的模糊划分也随之改变。

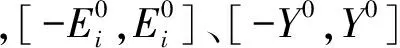
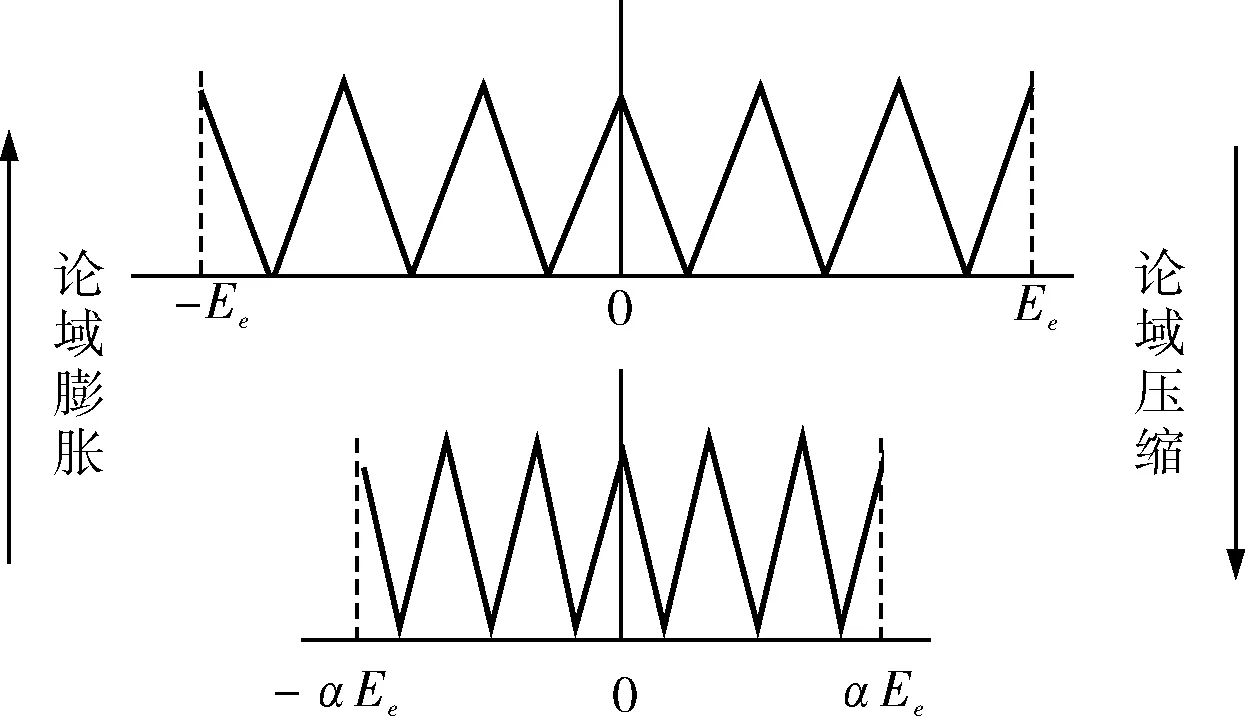
图2 e的论域变化

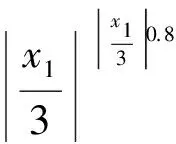
以正态云作为输入/输出语言值的隶属函数，对于输入变量e，期望Ex=x，熵En(xi+1-xi)/3(i=1,2,…，6)，超熵He为常数C，则En′=En+C·rand(1)；输出语言值隶属函数的设计相同。以e和Δki为例，图3给出了初始论域下输入e、输出Δki的隶属云曲线。

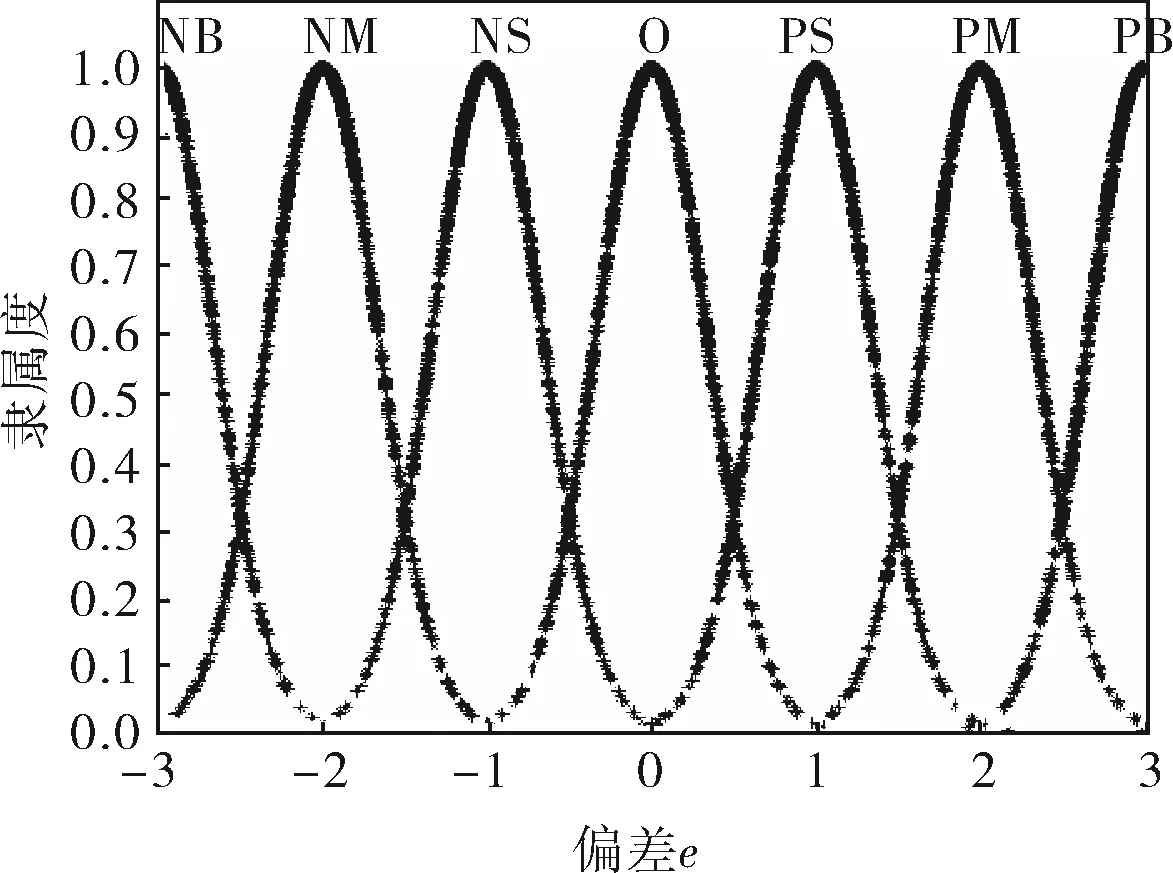
a. e正态云

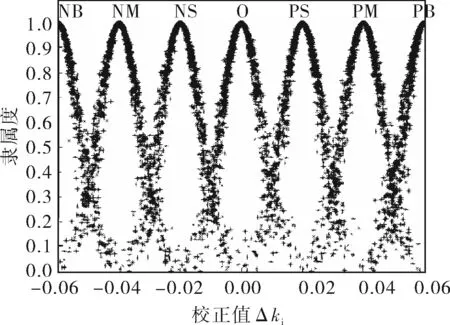
b. Δki正态云

3 仿真结果与分析

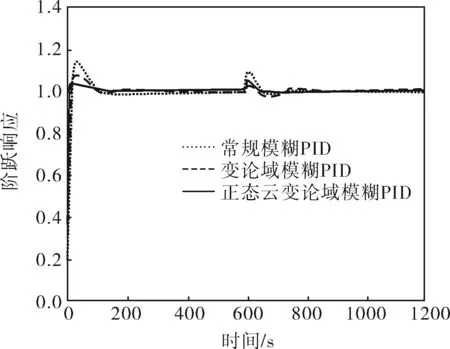
对300MW循环流化床机组在不同负荷下的模型进行Matlab仿真实验，位置指令为幅值为1.0的阶跃信号，采样周期为0.1s，仿真时间为300s。在600s时加入扰动信号，扰动信号的大小为阶跃信号的50%。对常规模糊PID、变论域模糊PID、正态云变论域模糊PID的控制特性进行比对，控制特性如图4所示，控制效果见表2。

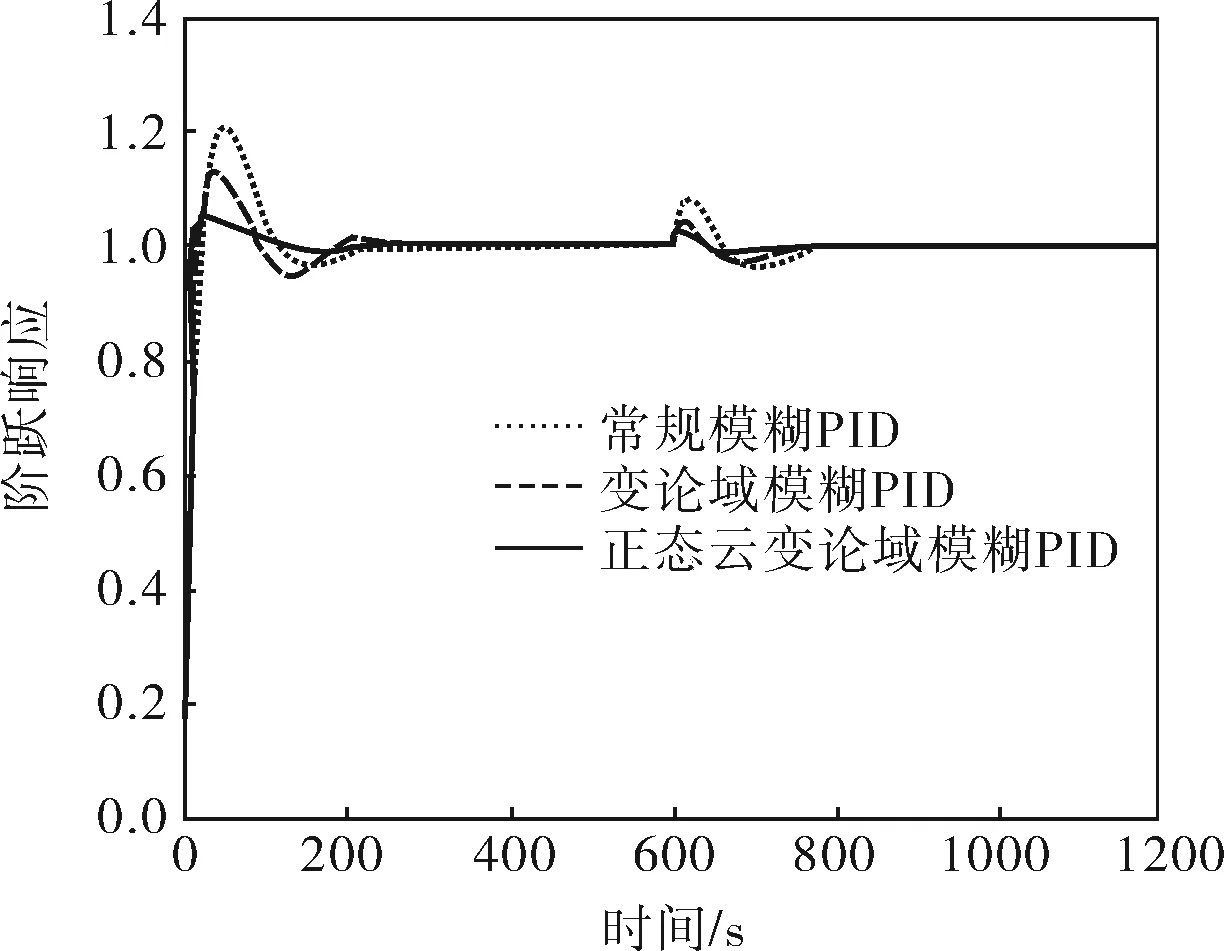
a. 100%负荷

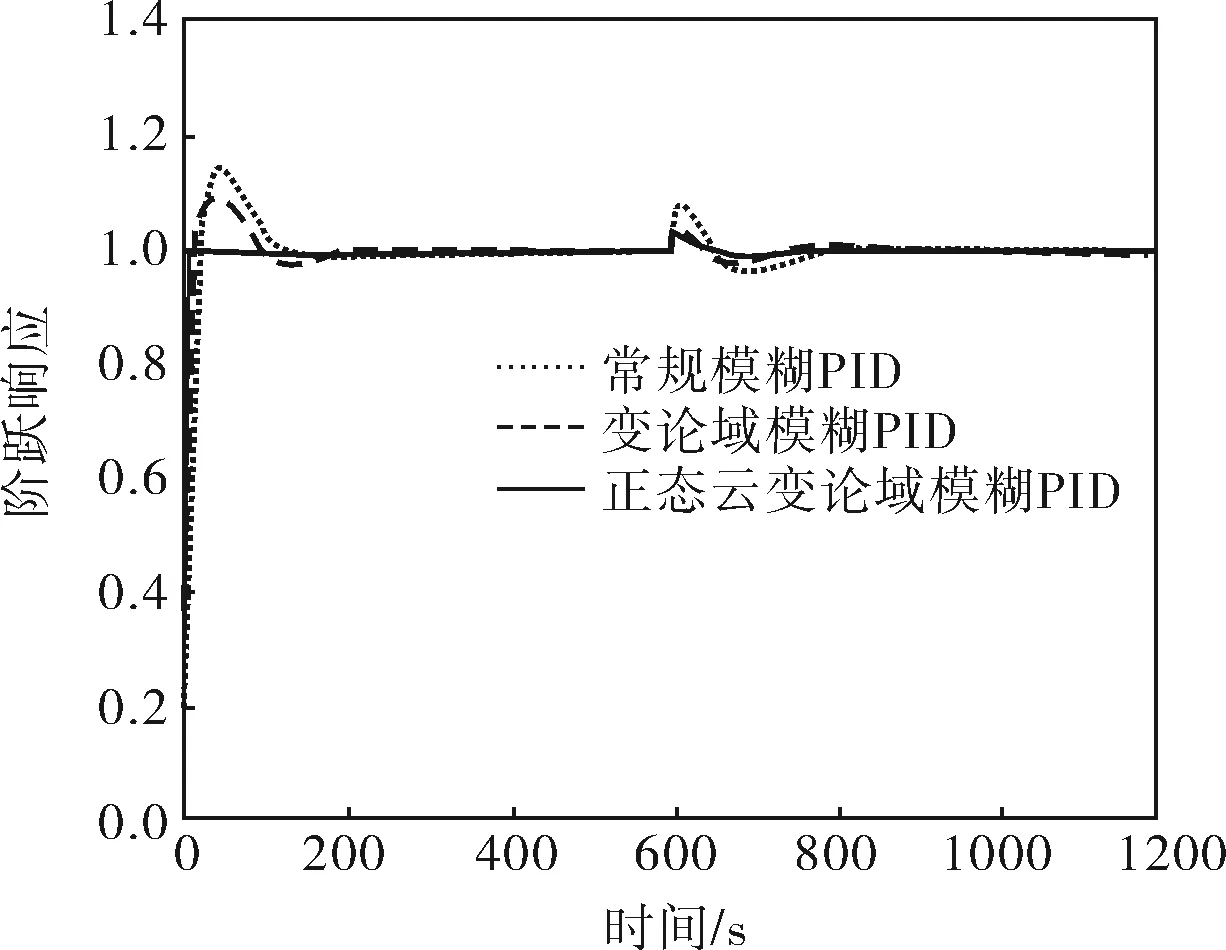
b. 87%负荷

c. 72%负荷

d. 57%负荷

控制方法100%负荷87%负荷72%负荷57%负荷tr/sts/sσ/%t/str/sts/sσ/%t/str/sts/sσ/%t/str/sts/sσ/%t/s常规模糊PID17．3748．221．291．614．7743．714．791．412．5740．213．31．520．1754．423．851．5变论域模糊PID9．7699．613．415．77．9694．99．035．76．5692．47．385．811．4703．416．335．8正态云变论域模糊PID5．2617．14．952．74．0615．93．022．73．2615．32．682．76．3618．05．952．7

注：tr——上升时间；ts——调节时间；σ——超调量；t——运行时间。

如图4所示，在外部扰动作用下，系统在不同负荷下均具有适度的阻尼、较快的响应速度和较短的调节时间，采用正态云变论域模糊PID方法获得的上升时间和超调量指标更优，且能保证系统在较短的时间内恢复稳定，相对于前两种控制具有更强的鲁棒性。在程序运行时长方面，相同条件(相同的计算机负担)下的仿真表明， 常规模糊PID方法不需要判断当前状态再进行论域的伸缩变化，使得其具有快速运行优势；而正态云变论域模糊PID方法采用正态隶属云取代隶属函数，利用云滴实现定量定性的不确定转换，不需精确复杂的隶属度计算过程，相较于变论域模糊PID方法的运行速度有较大提升。图5给出了输出变量的论域伸缩因子自适应变化曲线。

由图5可以看出，随着控制过程的进行，伸缩因子逐渐减小，使得模糊规则不断细化，在600s加入扰动作用时刻，伸缩因子突增后又逐渐减小，即控制规则根据e和ec的变化不断增加或减少。

4 结束语

通过在循环流化床炉内脱硫系统中的应用对比分析，验证了可变论域的正态云模糊PID控制方法的优势性能。相同条件下的仿真结果表明，在不同负荷的扰动作用下，所获得的动态性能更优(更快的响应速度、更小的超调)，鲁棒性更好，该方法为此类系统的优化设计提供了参考。

图5 伸缩因子的自适应变化曲线

[1] 韦丽娟.循环流化床锅炉脱硫的模糊控制[D].杭州：浙江大学，2008.

[2] Hao X W, Ma C Y, Dong Y. Composite Fluidization in a Circulating Fluidized Bed for Flue Gas Desulfurization[J]. Powder Technology, 2012， 215-216：46～53.

[3] Cheng H X, Zhang D S, Cheng L. Comparative Study on Fuzzy PID Controller and Conventional PID Controller[J]. Applied Mechanics and Materials, 2013, 328: 112～116.

[4] 李洪兴. 变论域自适应模糊控制器[J]. 中国科学: E辑, 1999,29(1):32～42.

[5] 郭海刚， 李洪兴， 胡凯. 一类变论域自适应模糊控制器[J]. 模糊系统与数学，2011，25(6)：1～9.

[6] 赵国亮，张永立，李洪兴. 区间II型变论域自适应模糊逻辑控制器[J].大连理工大学学报，2012，52(6)：914～920.

[7] 袁学海，李洪兴，宋晶晶. 基于区间值模糊点和区间值模糊临属关系的区间值模糊子群[J]. 模糊系统与数学，2014，28(1)：1～8.

[8] 李春晖.300MW循环流化床炉内脱硫控制系统的研究[D].北京：华北电力大学，2011.

[9] 杨鲜鲜，宁铎.变论域模糊PID控制器的设计与仿真[J].化工自动化及仪表，2010，37(4):29～32.

[10] 李德毅，刘常昱. 论正态云模型的普适性[J].中国科学工程，2004，6(8)：28～34.

[11] 李德毅，刘常昱，淦文燕. 正态云模型的重尾性质证明[J].中国科学工程，2011，13(4)：20～23.

[12] 李德毅， 杜鹢. 不确定性人工智能[M].北京：国防工业出版社，2014.