基于新型趋近律的永磁同步电动机滑模变结构控制
2015-01-13毕坤,邵民
毕 坤,邵 民
(新乡职业技术学院,新乡453006)
0 引 言
永磁同步电动机(以下简称PMSM)具有结构简单、功率密度高、体积小等优点,在很多领域得到了广泛应用。目前,由于传统的PID 控制器具有算法简单、可靠性高等优点,从而得到了普遍使用。然而由于永磁同步电动机具有强耦合性、参数时变性以及非线性等特点,当系统参数发生变化或者受到外界不确定因素的影响时,传统的PID 控制已经不能很好地满足控制器性能的要求[1]。为了提高PMSM控制性能并解决传统的PID 控制的不足,国内外研究者提出了反馈线性化控制[2]、神经网络控制[3]、自适应控制[4]、模糊控制[5]以及滑模变结构控制[6]等。其中滑模控制因其具有快速动态响应以及对参数时变性和外部扰动不敏感的特点,得到广泛应用。
为了提高PMSM 控制系统整体性能,在分析传统的趋近律滑模变结构的基础上,提出了一种新型滑模变结构趋近律。利用李雅普诺夫函数对新型滑模趋近律进行了稳定性分析;同时基于新型趋近律设计了速度控制器,将其应用到PMSM 调速系统中。仿真结构表明:该控制器能够提高控制系统鲁棒性和趋近速度,有效抑制了滑模控制中的抖振现象。
1 PMSM 数学模型
通过Park 变换,将两相静止坐标系中的电机变量变换成两相旋转d-q 坐标系中的变量,得:
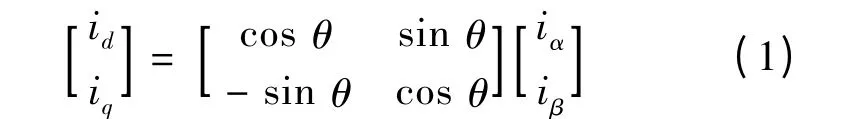
相应的Park 反变换:
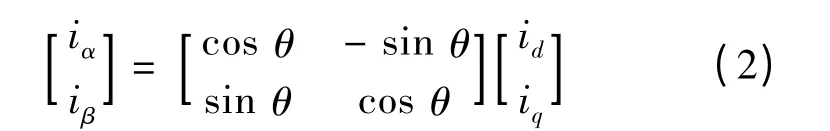
由此可以得到PMSM 在dq 坐标系下的电压方程:
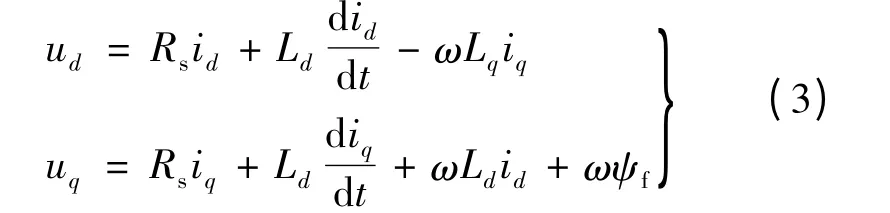
PMSM 转矩方程:

PMSM 运动方程:
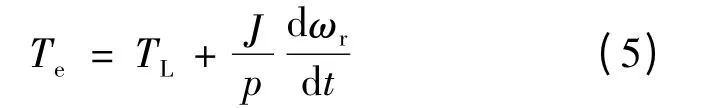
式中:id,iq和uq,ud分别为电机d 和q 轴电流和电压;R 为定子电阻;L 为定子电感;ψf为电机的永磁通;p 为极对数;J 为转动惯量;ω 为角速度;θ 为转子位置。
2 新型趋近律
滑模变结构控制系统的运动主要有两部分构成,如图1 所示,分别为趋近运动和滑模运动[7-9]。普通的滑模变结构控制只要求控制系统能够趋近滑模平面,但该控制方法不能反映通过何种方法趋近滑模平面,而趋近律法能够确保电机系统在滑模趋近运动阶段的性能。因此为了提高滑模趋近运动过程中的性能和抑制滑模抖振现象,对电机控制系统采用趋近律的方式进行控制[10]。
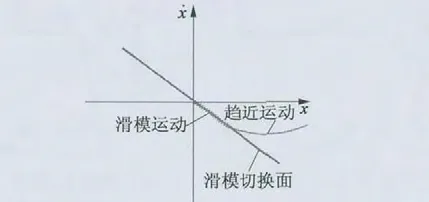
图1 滑模控制运动轨迹
2.1 等速滑模趋近律
等速趋近律如下:
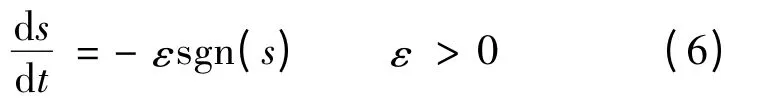
式中:s 为切换函数;ε 表示系统的运动点趋近切换面s 速率,为常数。趋近运动阶段的趋近速度为等速,趋近速度的可以通过参数ε 的调整进行改变。当参数ε 变大时,趋近速度增大;当参数ε 变小时,趋近速度减小。
设PMSM 滑模控制系统的状态变量:
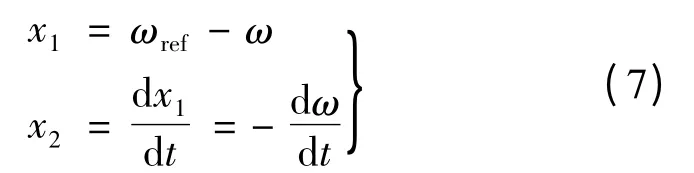
式中:ωref为电机期望转速;ω 为电机实际转速。
根据PMSM 运动方程和转矩方程可得:
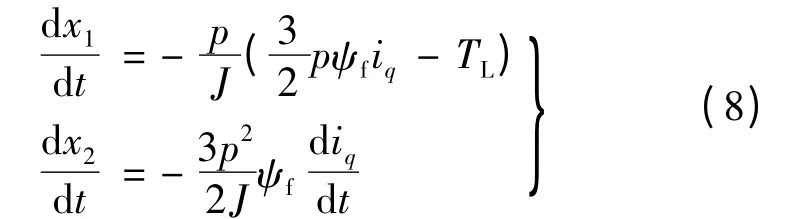
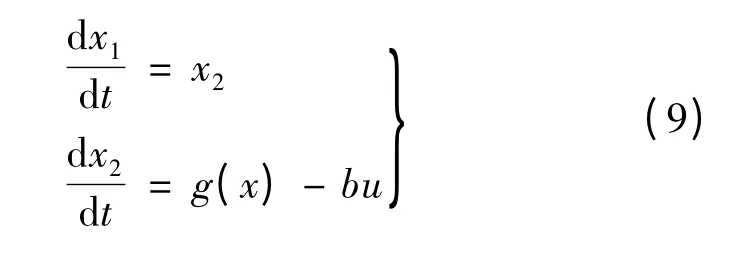
选择线性滑模切换面设计滑模控制器,线性滑模切换面表达式:

式中:c >0。采用等速趋近律设计的滑模控制输出:
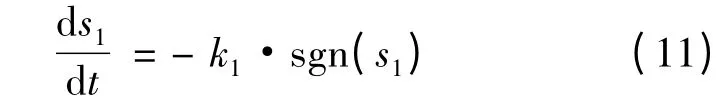
将式(10)代入式(11),可得:
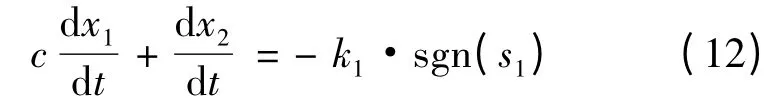
将式(9)代入式(12)得:
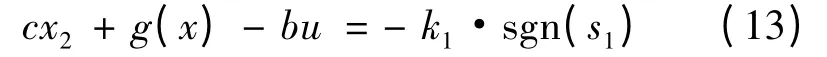
由此可得系统控制输出:
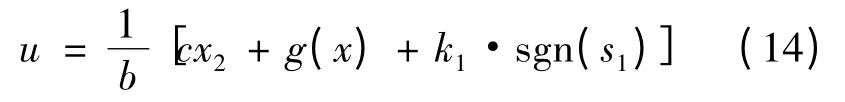
对式(11)两边同时积分可以得等速趋近律下趋近滑模切换面所用时间:

2.2 新型等速趋近律
新型趋近律如下:
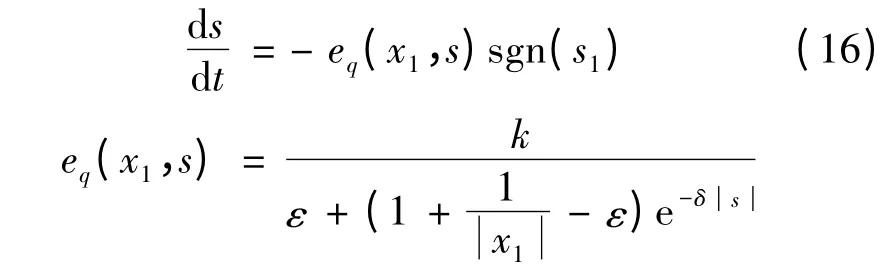
式中:k >0 为反映s 变化率的比例系数;δ >0 为指数趋近系数,用来控制指数趋近速率;0 <ε <1 为趋近切换面s 的速率。
2.3 新型等速趋近律稳定性分析
Lyapunov 函数定义[11]:

对式(22)进行积分并将式(16)代入其中,可得:
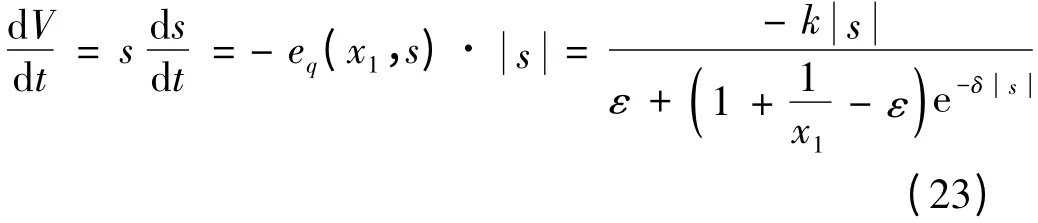
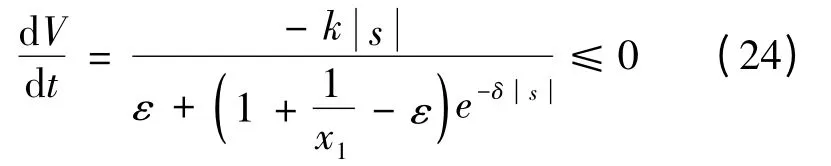
由此可以看出,该新型趋近律能够保证系统运动在有限时间内到达滑模切换面。
3 控制器设计
新型趋近律的滑模变结构控制结构如图2 所示。
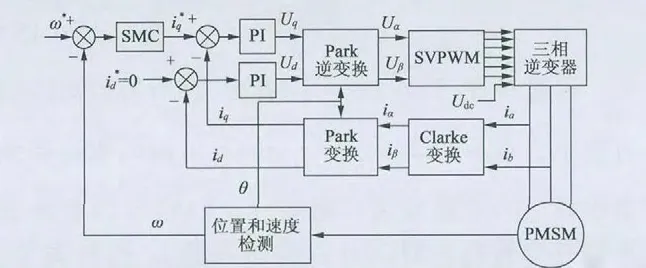
图2 新型趋近律的滑模变结构控制结构
假设速度跟踪误差:

式中:ωref为电机期望转速;ω 为电机实际转速。
设计滑模切换面:
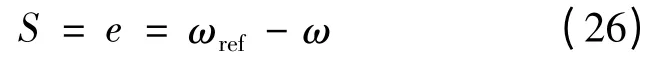
对式(26)求微分可得:
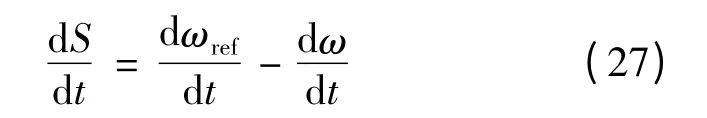
由PMSM 运动方程和电磁转矩方程可得:
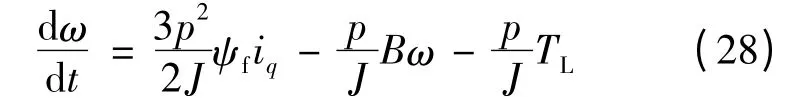
将式(28)代入到式(27)中,可得:
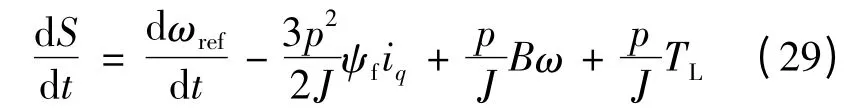
将新型趋近律代入式(29),得:
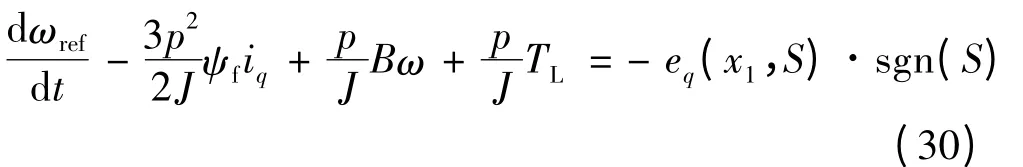
由此可得控制系统输出:
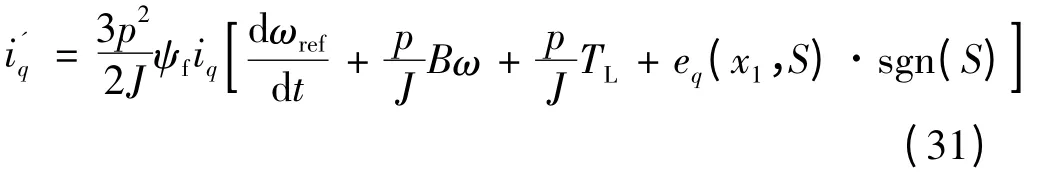
式(31)便是基于新型趋近律的PMSM 滑模速度控制器输出。
4 仿真实验
为验证上述算法的可行性,仿真实验主要对PMSM 调速系统采用传统的等速趋近律控制器和改进后的新型趋近律控制器进行仿真对比,电机的主要参数如表1 所示。
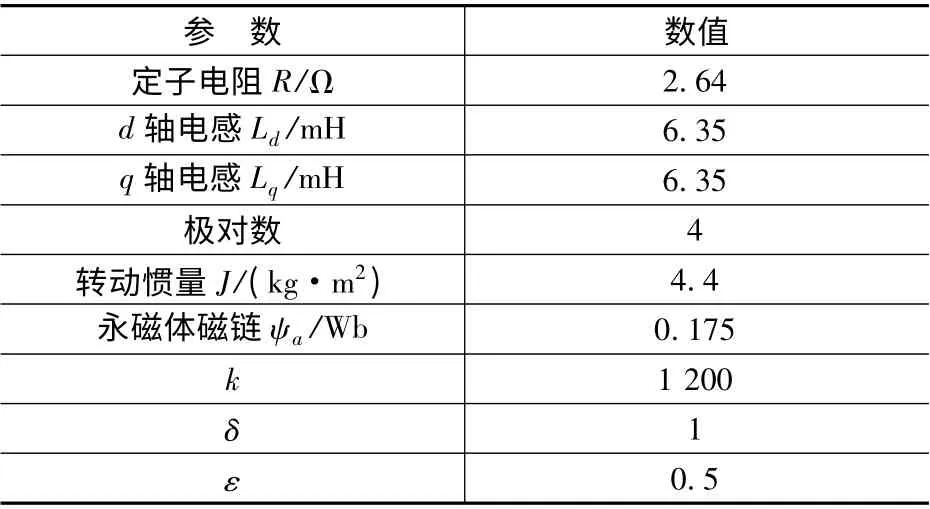
表1 控制器主要参数
当系统起动和突然负载时,采用这两种控制方式时对比曲线如图3 所示。图3(a)、图3(b)为系统起动时转速对比曲线,其余为当负载突然减小到0 时转速响应、三相电流对比曲线。
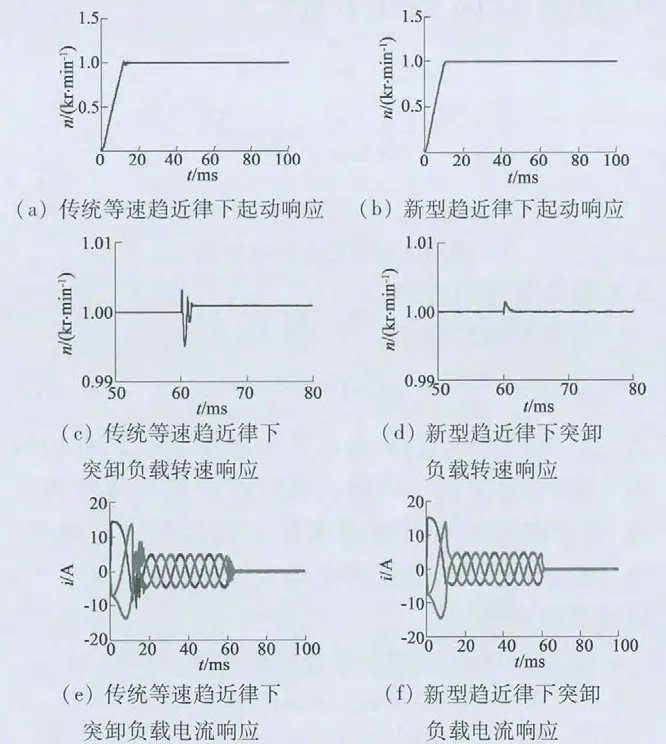
图3 两种趋近律下的控制对比
由仿真结果可以看出,当采用传统的等速趋近律进行控制时,系统转速、电流有明显波动,且存在稳态误差;而采用新型趋近律进行控制时,系统转速更加平稳,电流波形更加平滑,具有较强的抗外界干扰能力,鲁棒性更好。
5 结 语
本文在分析传统等速趋近律在控制过程中存在一定缺陷的基础上,提出了一种新型趋近率滑模变结构控制方法。利用李雅普诺夫函数对新型滑模趋近律进行了稳定性分析;同时结合新型趋近律,设计了基于新型趋近律的滑模变结构速度控制器。最后通过仿真实验对该方法进行了验证,仿真结果表明,新型趋近律可以有效抑制抖振现象,提高了趋近速度,提高了系统的鲁棒性,使得电机系统更加稳定。
[1] 曹先庆,朱建光,唐任远. 基于模糊神经网络的永磁同步电动机矢量控制系统[J].中国电机工程学报,2006,26(1):137-141.
[2] 田艳丰,郭庆鼎.永磁直线同步电动机的滑模-H∞鲁棒跟踪控制[J].电工技术学报,2004,19(4):1-5.
[3] 王焕钢,徐立文,黎坚,等.一种新型的感应电动机直接转矩控制[J].中国电机工程学报,2004,24(1):107-111.
[4] CHANG S H,CHEN P Y,TING Y H,et al.Robust current controlbased sliding mode control with simple uncertainies estimation in permanent magnet synchronous motor drive system[J].IET Electric Power Application,2010,4(6):441-450.
[5] KARUNADASA J P,RENFREW A C.Design and implementation of microprocessor based sliding mode controller for brushless servo motor[J].IEE Proceedings-B,1991,138(6):345-363.
[6] 曹先庆,朱建光,唐任远.基于模糊神经网络的永磁同步电动机矢量控制系统[J].中国电机工程学报,2006,26(1):137-141.
[7] LAGHROUCHE S,PLESTAN F,GLUMINEAU A,et al .Robust second order sliding mode control for a permanent magnet synchronous motor[C]//Proceedings of the American Control Conference. Denver,USA:American Automatic Control Council,2003:4071-4076.
[8] 张国柱,陈杰,李志平.直线电机伺服系统的自适应模糊摩擦补偿[J].电机与控制学报,2009,13(1):154-160.
[9] BAIK I C,KIM K H,YOUN M J.Robust nonlinear speed control of PM synchronous motor using boundart layer intrgral sliding mode control technique[J]. IEEE Transactions on Control Systems Technology,2000,8(1):47-54.
[10] 陈荣,邓智泉,严仰光.永磁同步伺服系统电流环的设计[J].南京航空航天大学学报,2004,36(2):220-225.
