改进人工蜂群算法在飞轮电机控制中的应用

毕文骏

(西南交通大学，成都610031)

0 引 言

飞轮储能系统(以下简称FESS)以其高能量密度、绿色环保、快速充电、对工作温度要求低等优点在风力发电、电动汽车等行业具有较高的应用价值。作为FESS 重要研究对象，飞轮电机控制系统存在多变量、强耦合、非线性等特点，传统PID 控制器性能难以达到最优［1］。同时，随着智能控制思想日渐成熟，结合智能控制以改善PID 在时变性上的缺陷具有较高的学术和实用意义。文献［2］在永磁无刷直流电动机转速外环PID 中选用蚁群算法(以下简称ACO)优化，取得了良好的效果。文献［3］应用了遗传算法(以下简称GA)，也使得PID 控制器的性能得到了改善。文献［4］运用经典人工蜂群算法(以下简称ABC 算法)对PID 进行参数整定，证明并体现了其相较于其他智能优化算法，具有更为优秀的收敛特性和优化特性。但ABC 算法仍旧存在易陷入局部最优、后期收敛缓慢、精度不高等缺陷［5］。

针对上述缺点，本文在经典ABC 算法的基础上引入自适应系数(自适应ABC 算法，以下简称A－ABC 算法)，使得在对系统外环PID 控制器参数整定过程中，能够自适应地调节寻优策略，协调了算法的全局搜索能力与特定区域寻优能力。

1 飞轮电机控制系统

FESS 重要组成部分如图1 所示。当直流电能过剩时，多余的电能经由变流器带动飞轮电机转动，最终转化为飞轮的动能;当直流电能供给不足时，飞轮释能，通过变流器将能量反馈给直流母线。经分析可知，飞轮电机控制系统是飞轮储能系统的重要组成部分。

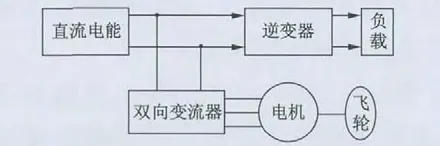
图1 FESS 基本工作原理图

本文选择无刷直流电动机作为飞轮电机，采用转速－电流双闭环控制系统，控制框图如图2 所示。它由传感器、双向变流器和电机等部分组成，采用励磁电流为零(=0)的控制策略实现最大转矩控制［4］，此时电磁转矩Te正比于转矩电流分量iq。

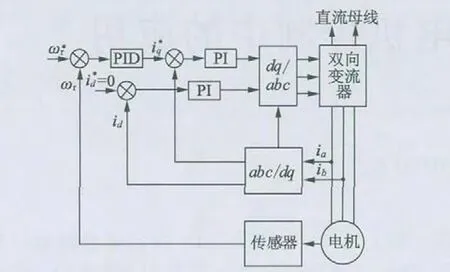
图2 电机控制框图

在系统中，位置传感器采集转子信息，计算得到ωr(转子速度);PID控制器的输入即为ωr(转子速度)与(转速给定参考值)的差值，并输出(电流内环参考值);经abc/dq 变换后得到d 轴和q 轴定子电流值，分别与参考值比较后作为PI 控制器的输入;输出d 轴及q 轴电压，经坐标变换后得到三相电压合成的空间电压矢量;最终通过变流器实现电机转速的控制。

通过分析电机控制系统可知，该系统被控对象是一个二阶系统模型［6］:

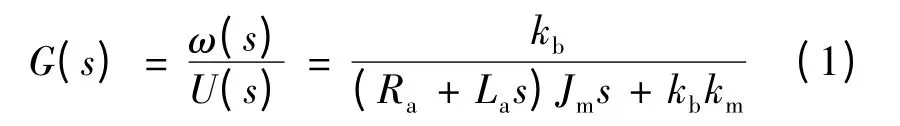
式中:ω 为机械角速度;U 为直流电压;kb为反电势系数;km为力矩系数;Ra为电枢电阻;La为电枢电感;Jm为转动惯量;

因此，对此二阶系统的PID 控制器设计及优化具有重要意义。而优化PID 控制器的工作重点主要体现在对PID 三个参数Kp，Ki，Kd的整定。传统的整定方法步骤繁琐，工作量大，难以达到理想效果;同时在被控对象改变时需要重新整定参数。基于以上问题，本文将智能优化算法应用于PID 控制器参数整定，从而优化PID 控制器性能。

2 ABC 算法

ABC 算法是一种模拟蜂群行为的智能优化算法，于2005 年由Karaboga 提出。因为ABC 算法具有较强的全局性、并行性以及能够较好的结合其他智能算法，近年来为广大科研工作者所关注。文献［7－10］从多种角度证实了ABC 算法较于传统的生物智能算法有较强的竞争力。

ABC 算法中，解空间内的各个可能解用蜜源表示，衡量蜜源优劣程度以适应度函数值衡量。蜜蜂按不同分工可分为3 种:采蜜蜂、跟随蜂以及侦查蜂(采蜜蜂和跟随蜂各占蜂群总数的一半，对应于劣质蜜源的采蜜蜂转化为侦查蜂搜索新蜜源)。具体对蜜源的搜索如下:

(1)算法初始化。采用随机的方式，产生n 个初始解，即为蜜源:

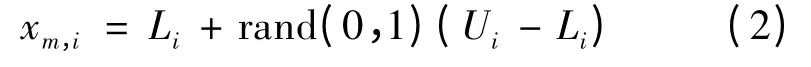
式中:每个蜜源的位置用xm，i表征，m=1，2，3，…，n。Li和Ui算法空间的下界和上界。蜜源数量等于采蜜蜂数量，蜜源循环搜索次数即为寻优迭代次数。

(2)侦查蜂发现蜜源，并测量蜂蜜量(适应度值)。适应度值fxm计算公式:

式中:J 为评价函数，由研究模型决定。

(3)跟随蜂依据采蜜蜂所提供的蜜源信息，通过收益度值选择蜜源采蜜。某个蜜源被跟随蜂选择的概率:

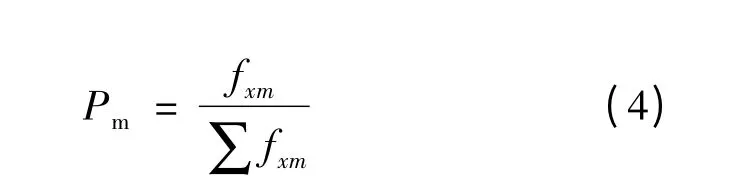
(4)若蜜源经过“限定次数L”次后没有得到更新，则放弃该蜜源;同时对应于该蜜源的采蜜蜂转化为侦查蜂，根据式(2)产生新的蜜源。

3 A-ABC 算法

在群体智能优化算法中，可以用探索能力和开发能力衡量算法的优化性能［11］。探索能力是算法在全局中对不同区域搜索较好解的能力，开发能力是在特定区域进一步提炼较好解的能力。

ABC 算法中，采蜜蜂根据蜜源邻域位置搜索公式在蜜源附近搜索适应度值更高的蜜源。经典ABC 算法所采用的领域位置搜索公式:

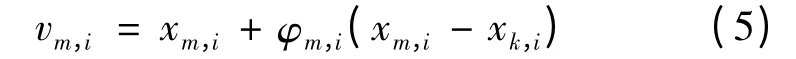
式中:k 为不同于i 的解;φ 为［－1，1］之间的随机数。

式(5)因其选择的随机性而使得经典ABC 算法具有较强的探索能力，但开发能力较差，存在收敛速度慢、搜索精度差等问题。针对这一问题，本文在文献［11］的基础上，引入自适应系数对经典ABC 算法邻域位置搜索方程进行改进，即:

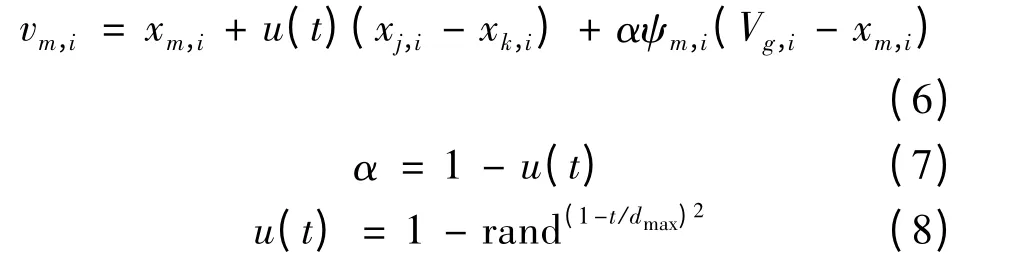
式中:m，i，k 的选取参见式(2);ψm，i∈［0，1.5］;当前循环下全局最优解用Vg，i表征;dmax为最大循环次数;u(t)为自适应系数，t 为当前循环次数，随着算法循环次数的增加，u(t)在不断的改变算法探索与开发之间的权重。当循环开始时，u(t)≈1，此时算法在探索方面具有较高权重，全局搜索能力得到加强，从而不易于陷入局部最优;随着t 的不断增大，自适应系数u(t)的取值逐渐减小，此时算法倾向于对全局最优解引导下的区域进行开发，增进了算法的收敛速度与精度。

因此，改进的ABC 算法能够自适应地改变搜索方程内各个影响因素的权重，从而使得算法同时具备较好的探索能力与开发能力。

4 PID 控制器设计

将电机转速环PID 控制器的比例、积分及微分参数(Kp，Ki，Kd)作为改进ABC 算法的一个蜜源。为了获得理想的过渡过程动态特性，引入了三个主要的评价指标，分别是时间乘误差绝对值积分(ITAE)，最大过冲(OS)和建立时间(ST)。ITAE(时间乘误差绝对值积分)的表达式:

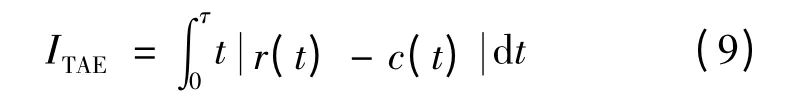
式中:c(t)是t 时刻的输出值;r(t)是t 时刻的预设值。ITAE用于评价控制器误差的总和，误差越小，则ITAE值越低。

OS的计算公式:

式中:cmax表示输出c 的最大值;css是输出c 的目标值。OS用于衡量控制器限制最大输出的能力，取值越低，则PID 控制器越能够稳定的建立对目标值的跟踪。

系统的输出值与目标值之间的差距小于5%所需的时间为ST。ST可以衡量系统对目标建立有效跟踪的速度。

当系统为二阶系统时，系统闭环传递函数:

式中:ζ 为阻尼系数;ωn为自然频率。根据文献［12］的结论可以得到:

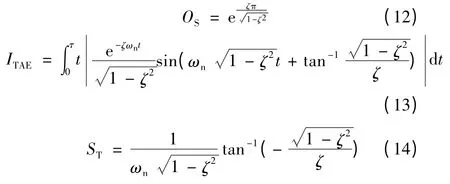
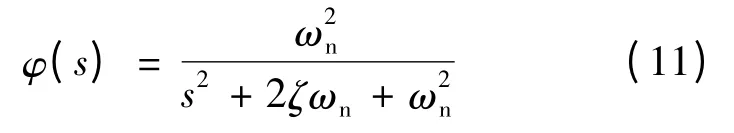
将上述三种评价指标以下式的形式作为系统性能评价函数:

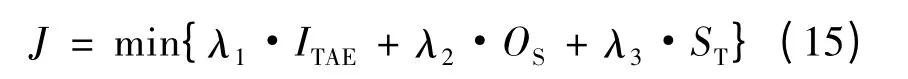
式中:J 为评价函数值。当J 的值最小时，性能最优。λ1，λ2和λ3为待定系数。

从而，改进ABC 算法(A－ABC 算法)对电机控制系统PID 控制器参数整定步骤如下:

第一步，种群初始化。种群数量为n，最大迭代次数为dmax，搜索维数为Dim，限定次数为L。初始化种群空间。

第二步，适应度值计算。将种群空间每个行向量xm代入式(15)得到其评价函数值。根据所选评价函数特性与ABC 算法的特性，通过式(3)计算其适应度值fxm。

第三步，邻域搜索。通过邻域搜索寻找新蜜源。若新蜜源适应度值优于当前蜜源适应度值，则对蜜源进行替换操作。

第四步，对于跟随蜂，由式(4)计算得到的概率值选择蜜源并进行邻域搜索产生新解，选择适应度值更为优秀的蜜源。

第五步，若限定次数L 内仍然没有找到更优秀的蜜源，则放弃该蜜源，并根据式(2)随机生成一个新的蜜源。

第六步，保存当前所有蜜蜂找到的最优蜜源(全局最优解)，判断算法终止条件(最大迭代次数)。若满足条件，则返回PID 控制器的三个参数(Kp，Ki，Kd)，算法终止。否则返回第一步继续算法。

算法寻优流程图如图3 所示。

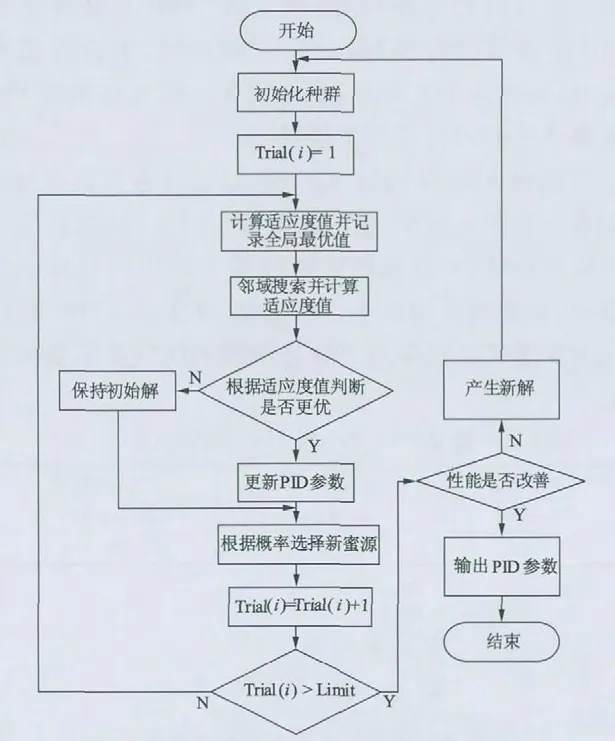
图3 飞轮电机PID 参数整定流程图

5 仿真分析

为了验证本文选用的A－ABC 算法的性能，在MATLAB/simulink 环境下搭建仿真平台。系统内参数设计如下:电枢电阻Ra=0.025 3 Ω;电枢电感La=9.8 mH;力矩系数Km=1 N·m/A;反电势系数Kb=326 V/(rad·s－1);转动惯量Jm=0.5 kg·m2;种群数量n =20;最大迭代次数dmax=100;搜索维数Dim=3;限定次数L =10;ITAE权重系数λ1=1;OS权重系数λ2=30;ST权重系数λ3=1。此时系统中被控对象传递函数:

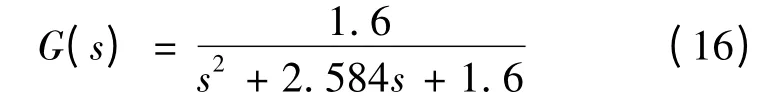
分别采用GA、ABC 算法与A－ABC 算法对PID参数进行优化。优化结果如表1 所示。图4 给出了不同算法优化下的飞轮电机的阶跃响应曲线。

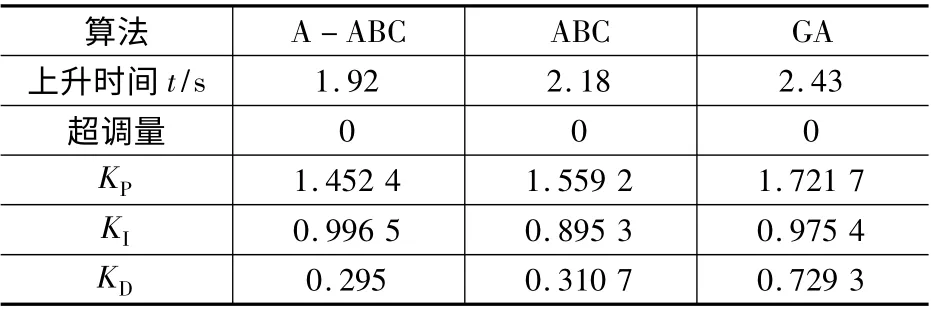
表1 不同算法优化的PID 控制器

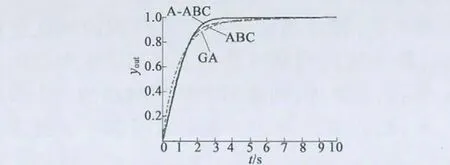
图4 PID 控制器在不同算法下阶跃响应曲线图

经过比较分析可知，基于A－ABC 算法优化的PID 控制器性能较好，上升时间最短，不存在超调量，从而验证了A－ABC 用于飞轮电机充电系统PID 参数优化的可行性与优越性。

经典ABC 算法与A－ABC 算法的迭代收敛对比如表2 及图5 所示。在迭代过程中，A－ABC 算法能够较快收敛，并且最终能够收敛于较小的目标函数值，从而表明了相对于经典ABC 算法，A－ABC算法在飞轮电机系统中对PID 控制器的优化效果更加突出。

表2 A－ABC 与ABC 迭代对比

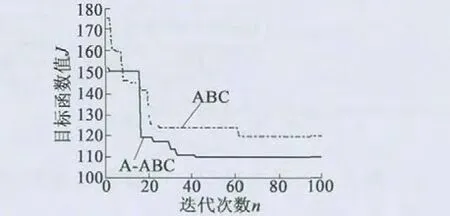
图5 算法迭代收敛图

6 结 语

本文将A－ABC 算法应用于飞轮储能PID 控制器中，实现了PID 参数的整定优化。仿真结果证明，采用该算法的PID 控制器具有较快的上升时间且不存在超调量，并且相对于经典ABC 算法，该算法具有更快的收敛速度与精度。

［1］ 尤晓玲，王能才.基于RBF 神经网络的智能车速度控制系统研究［J］.电气自动化，2015，(1):102－104.

［2］ 王贯安.基于蚁群算法的无刷直流电机PID 控制器测试系统［J］.电子技术，2010，47(4):64－66.

［3］ ZHOU Y，WANG Z，YANG L. Application of Fuzzy PID control based on GA in control valve［J］.Applied Mechanics＆ Materials，2014，668－669:445－449.

［4］ 曹文平，李伟华，王利鑫，等.人工蜂群算法在飞轮充电控制系统中的应用研究［J］.华东电力，2011，(9):1500－1504.

［5］ 赵辉，李牧东，翁兴伟.具有自适应全局最优引导快速搜索策略的人工蜂群算法［J］. 控制与决策，2014，29(11):2041－2047.

［6］ 王国富，陈良益，张法全，等.星载光电跟踪系统飞轮控制系统设计［J］.微计算机信息，2007，23(25):14－15.

［7］ AKAY B，KARABOGA D.A survey on the applications of artificial bee colony in signal，image，and video processing［J］.Signal Image ＆ Video Processing，2015，9(4):967－990.

［8］ KARABOGA D，GORKEMLI B，OZTURK C，et al. A comprehensive survey:artificial bee colony (ABC)algorithm and applications［J］.Artificial Intelligence Review，2014，42(1):21－57.

［9］ KARABOGA D，GORKEMLI B. A quick artificial bee colony(qABC)algorithm and its performance on optimization problems［J］.Applied Soft Computing，2014，23(5):227－238.

［10］ KARABOGA D，AKAY B. A comparative study of Artificial Bee Colony algorithm［J］. Applied Mathematics ＆ Computation，2009，214(1):108－132.

［11］ ZHU G，KWONG S. Gbest－Guided Artificial Bee Colony Algorithm For Numerical Function Optimization［J］. Applied Mathematics ＆ Computation，2010，217(7):3166－3173.

［12］ 赵冰.飞轮储能系统的智能控制研究［D］. 上海:东华大学，2008.

［13］ 吴建辉，章兢，李仁发，等. 多子种群微粒群免疫算法及其在函数优化中应用［J］.计算机研究与发展，2012，49(9):1883－1898.