改进Crowbar 电路的双馈电机三相短路参数整定

丁 磊，张建华，沈浩然，戴春蕾

(扬州大学，扬州225127)

由式(8)可知，在发生三相短路故障时，基波分量i1 以及谐波分量i(1－s)的幅值都很大。而直流分量很小，忽略不计。又因为采用的是标幺值，所以转子电流的大小与定子电流基本相同。在三相对称短路故障时转子回来中最大短路电流:

0 引 言

双馈感应发电机(以下简称DFIG)，因为它能够提高额定风速下风能捕获效率，获得最佳的能量输出，有功和无功可以单独调节等优点成为风电场中的主力机型，在风力发电系统中得到了广泛应用。然而，由于DFIG 定子直接与电网相连，转子经过变换器与电网相连，这就使得DFIG 对电网电压波动异常敏感。电网发生电压跌落故障时会导致DFIG转子绕组中电压过大，若不及时采取有效的保护措施，容易导致转子侧变频器中功率器件的损坏而且危及风电机组的安全运行。在电网故障中，三相短路故障时又是较为常见的一种，提高DFIG 电机在三相短路故障下的适应能力，已成为国内外研究的热点问题［8］。

在电网发生三相短路故障时，当前普遍采用的方法是为DFIG 转子侧配置Crowbar 电路［3－4］，通过Crowbar 电阻短接变换器达到保护电机的目的。然而，双馈电机转子侧通过Crowbar 电阻短接后，使得转子不具有励磁控制能力，双馈电机相当于普通的感应发电机运行。而作感应电机在运行时感应电机会从电网中吸收无功功率，不利于电网故障的恢复，严重时可导致双馈电机脱网运行，因此双馈电机不能参与电网电压故障过程中的系统功率调节，无法满足电网运行规程中对无功功率的要求，不利于暂态过程中电网电压的稳定性。为此，提出改进的Crowbar 电路以满足电压跌落过程中对无功功率的要求。改进的Crowbar 电路在结构上通过在定子回路中串接电感以改善以往Crowbar 电路不能向电网提供无功支持的缺点。本文在建立变速恒频双馈风力发电机短路过程数学模型的基础上，求得双馈发电机三相短路过程中的定子电流的解析表达式，在对双馈风力发电机三相短路瞬态分析的基础上，提出改进的Crowbar 电路参数整定的方法，最后通过MATLAB 进行仿真验证。

1 改进的Crowbar 电路介绍

双馈电机系统转子侧Crowbar 电路结构示意如图1 所示。

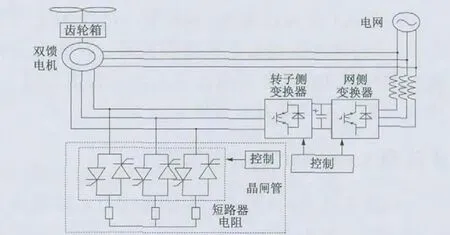
图1 转子Crowbar 电路DFIG 系统图

以往为保护电机采用的未改进的Crowbar［9］电路在发生电网电压跌落故障时，当检测到流过转子侧变化器的电流超过其所能承受的最大允许电流时，触发晶闸管导通短接变换器，使电流流经短路器电阻，从而达到保护转子侧变化器的目的。

改进的Crowbar 电路在电网发生跌落故障时，依据检测单元检测到电压跌落信号，将电压跌落信号传输给比较单元，比较单元根据跌落深度采取相应的保护措施(以本文三相短路为例)，比较单元向改进的Crowbar 电路发出控制信号，控制开关K 动作将Crowbar 电感串接到定子电感中，实现对双馈电机的保护。相比以往采用的Crowbar 电路改进的Crowbar 电路结构更加简单。改进Crowbar 电路后双馈电机系统结构示意如图2 所示。

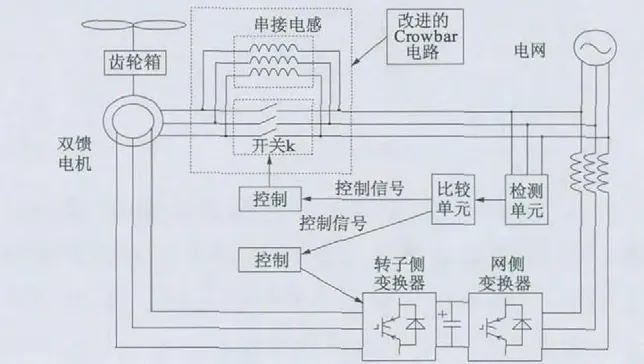
图2 改进Crowbar 电路后DFIG 结构图

比较图1、图2 可以发现，改进的Crowbar 电路区别于以往采用的Crowbar 电路主要在以下两方面:

1)所处的位置而言，以往采用的Crowbar 电路是配置在双馈电机的转子侧，而改进的Crowbar 电路则是配置在双馈电机的定子侧。

2)在结构方面，以往采用的Crowbar 电路是通过电阻短接变换器达到保护电机的目的，而改进的Crowbar 电路则是通过定子串接电感来限制电流达到保护目的。

在功能上，电网电压跌落故障下改进的Crowbar电路不但能够实现现有Crowbar 电路对双馈电机的保护要求，而且能够向电网提供无功支撑实现低电压穿越。

2 双馈电机数学模型

本文的DFIG 定、转子模型正方向均选取电动机惯例。根据文献［3］和文献［4］，可以得到DFIG定、转子在dq 旋转坐标系下的电压平衡方程如下:

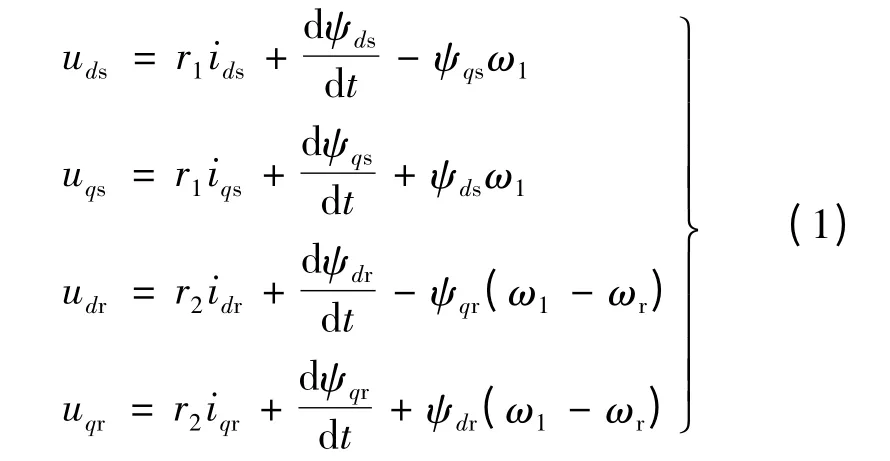
定、转子磁链方程:

式中:ids，iqs，idr，iqr是定、转子绕组中电流d，q 轴分量;uds，uqs，udr，uqr是定、转子电压d，q 轴分量;ψds，ψqs，ψdr，ψqr是定、转子磁链d，q 轴分量;ωr，ω1是转子角速度、同步角速度。

Ls=L1+ Lm，Lr= L2+ Lm，L1，L2是定、转子漏感;Lm是定子与转子绕组的互感。

将式(1)、式(2)消去磁链后得到DFIG 的状态空间方程如下:

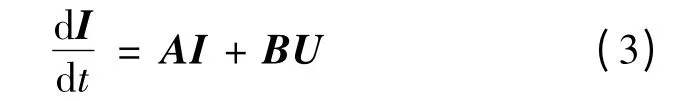
式中:I，U 分别为电流、电压列向量;A，B 为系数矩阵。

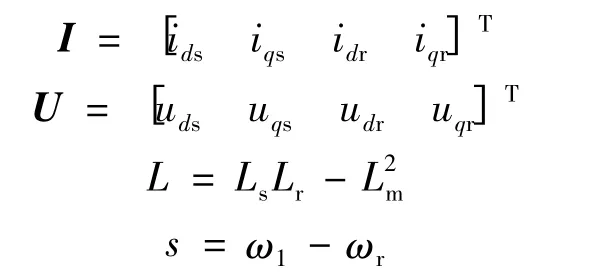
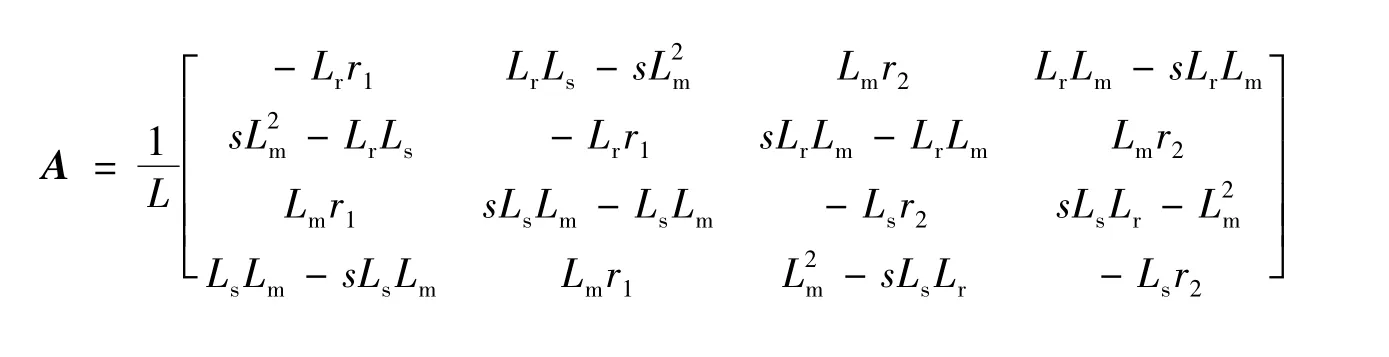
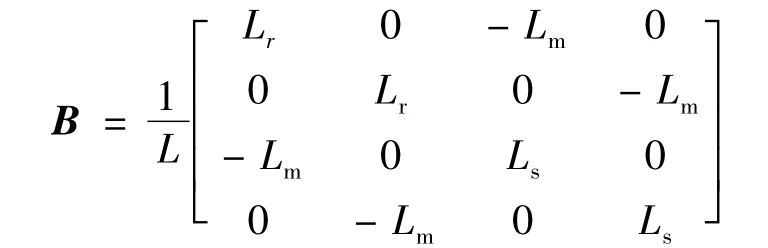
由于稳态运行时DFIG 定子电流中只含有恒定的工频分量，所以在d－q 旋转坐标下电压和电流分量均为常量，此时由式(3)得到的DFIG 在稳定运行时的关系式:

3 短路瞬态特性

在双馈电机的三相短路暂态过程的分析中，为了避免了数学描述电压突变问题，故将其转换成稳定运行状态与加反向电压的过渡过程的叠加。

3.1 DFIG 稳定运行的工况

在时域内对式(4)求解，可以解析得定子电流在dq 旋转坐标系下的表达式，再经坐标变换后得到稳定运行时定子电流的解析表达式。以定子A 相电流为例，稳定运行时定子电流的表达式:

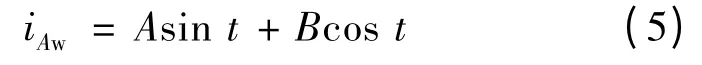
式中:

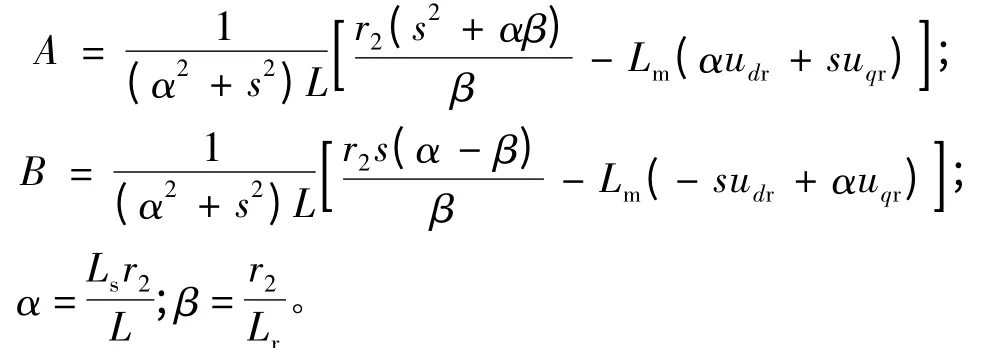
3.2 DFIG 加反向电压运行工况的分析

根据文献［16］可知，电压、电流列向量在满足式(3)约束条件下经过拉普拉斯变换可求得电流在dq 坐标系中随时间的变化规律。再经过坐标变换将dq 坐标系转换到ABC 坐标系下可求得短路时定子电流的变化规律。由于运算过程的复杂性，本文直接给出三相短路时A 相短路电流表达式:

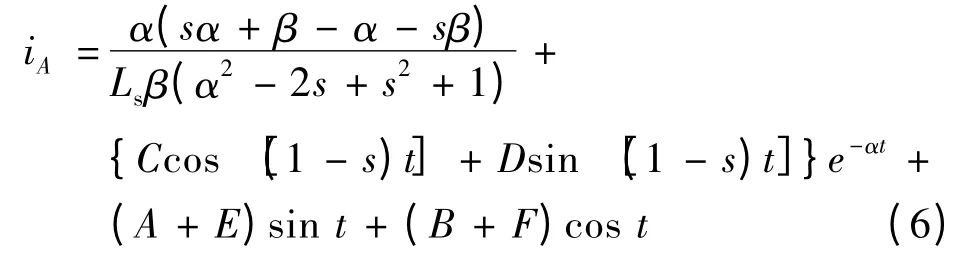
式中:

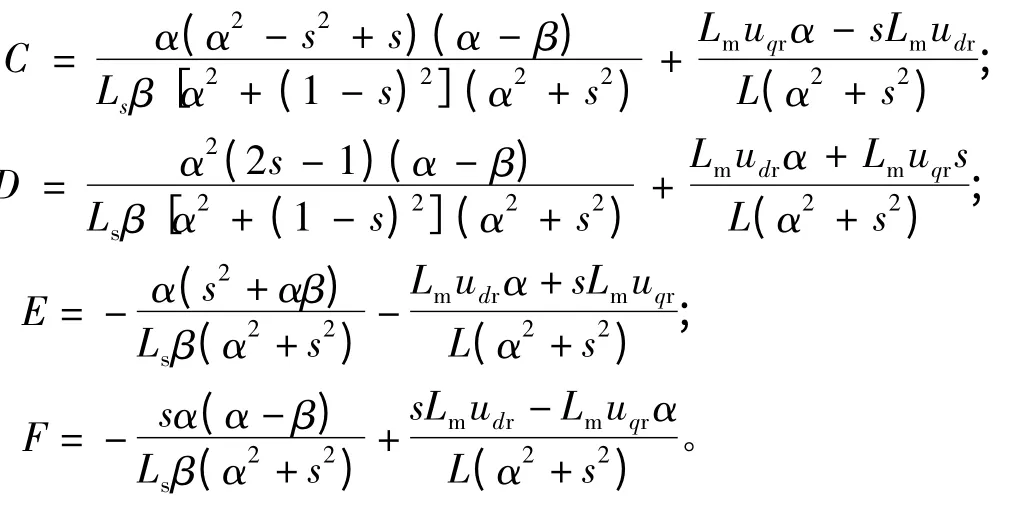
根据式(6)可以发现，该系数与电机的运行状态、转子励磁电压以及电机参数有关。在发生三相短路故障时DFIG 定子电流中出现了直流分量ia、谐波分量i(1－s)以及基波分量i1。

4 改进Crowbar 的参数整定

以往未改进的Crowbar 电路是通过电阻短接变换器达到保护电机的目的，故对Crowbar 的参数整定对短路电阻值的整定，而改进的Crowbar 电路则是通过定子串接电感限制电流来达到保护目的，故引入改进的Crowbar 电路的参数整定是对限流电感值的整定。

由于L1≪Lm，L2≪Lm，故α≫β。因为DFIG 运行时转差率很小，因此式(6)可以化简:

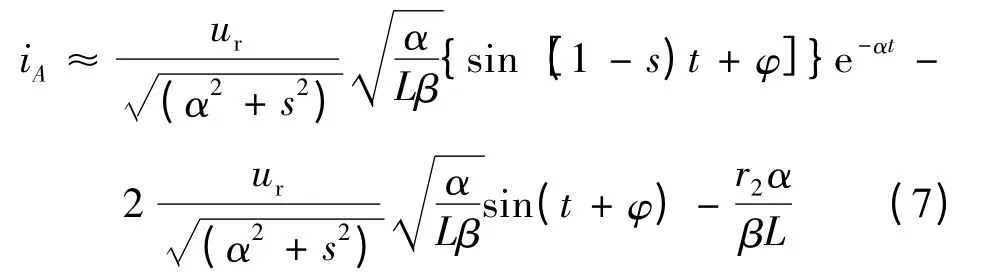
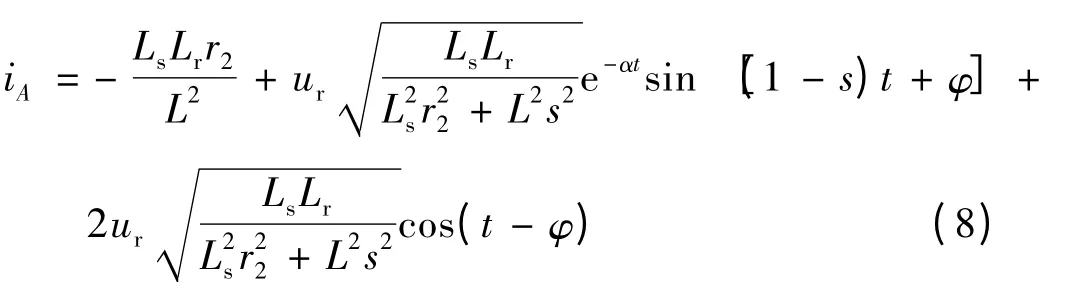
由式(8)可知，在发生三相短路故障时，基波分量i1以及谐波分量i(1－s)的幅值都很大。而直流分量很小，忽略不计。又因为采用的是标幺值，所以转子电流的大小与定子电流基本相同。在三相对称短路故障时转子回来中最大短路电流:

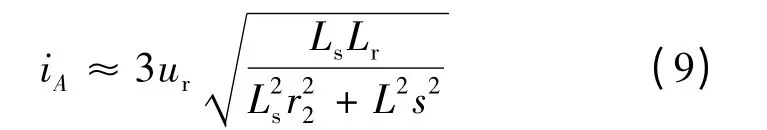
根据式(9)可以发现，电流的大小取决于定转子电感和转子电阻，故可通过在定子回路串电感构成改进的Crowbar 电路，在发生三相短路故障时起到限制短路电流的作用。这里由于参数整定的过程的复杂性，本文直接给出3 MW 的双馈感应电机整定后的Crowbar 电感参数数值为1.43 mH。

5 建模与仿真

为了验证理论分析的正确性，本文基于MATLAB/Simulink 平台，选取一台3 MW 的双馈感应电机为例进行仿真分析。DFIG 三相短路时仿真模型，如图3 所示。

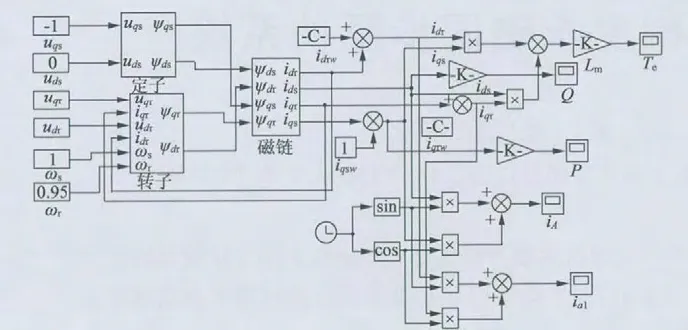
图3 双馈电机三相短路仿真模型

3 MW 双馈电机在标幺值下仿真参数如下:L1=0.007，L2=0.17，Lm=3.3，r1=0.007，r2=0.005;假设正常运行时电机功率因数为1，转差率s =0.05，双馈电机的转子电压udr=0.0137，uqr=0.0471。

图4 为双馈风力发电机三相对称短路时理论分析和建模仿真得到的定子电流iA的波形的比较。

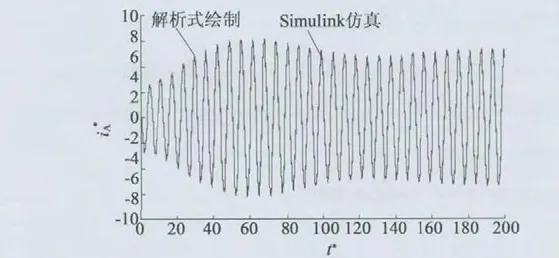
图4 定子A 相短路电流仿真波形

从图4 可以得知，两条曲线的变化规律相同，这说明本文所采用的分析方法的正确性。此外三相短路过程中定子电流幅值远大于额定电流，因此必须对双馈电机三相短路采取相应的保护措施。

采用改进的Crowbar 电路后双馈电机三相短路定子电流iA的仿真波形图，如图5 所示。

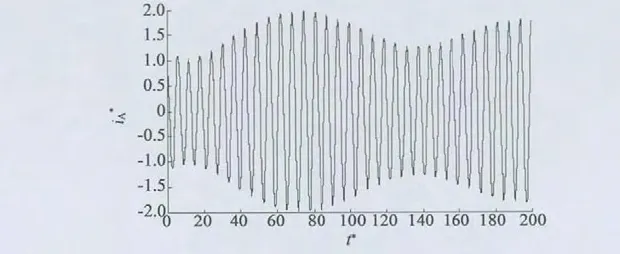
图5 改进Crowbar 电路作用后定子A 相短路电流仿真波形

从图5 中可以看出，通过改进的Crowbar 电路作用，可以实现对双馈电机的短路保护，说明了本文提出的这种改进的Crowbar 电路的可行性。

在仿真过程中选取的Crowbar 电路电感参数为1.43 mH，与理论分析的结果相一致，进一步说明了理论分析的正确性。

根据文献［9］中提出的现有的转子侧Crowbar电路，在三相短路故障时转子侧Crowbar 电路作用下定子A 相电流的仿真波形如图6 所示。

从图6 可知，在转子侧Crowbar 电路的作用下，发电机内部的短路电流可以得到抑制，其电流的峰值大约是短路前稳定运行时的电流值的2 倍。

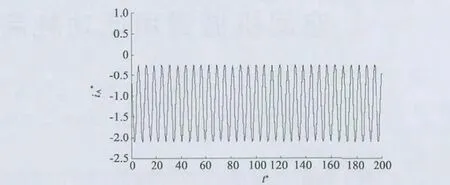
图6 未改进Crowbar 电路作用后定子A 相短路电流仿真波形

图7 给出的文献［9］中Crowbar 电路与改进的Crowbar 电路作用下定子A 相电流的对比图。

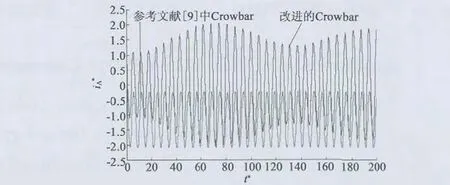
图7 两种Crowbar 电路分别作用定子A 相短路电流对比波形

从图7 可以看出，文献［9］中Crowbar 电路与改进的Crowbar 电路都能在短路故障下实现对双馈电机保护，而改进的Crowbar 电路实现的效果相对较好。

6 结 语

本文提出了一种改进的Crowbar 控制电路，实现了未改进的Crowbar 电路对DFIG 的保护要求。将短路的电磁暂态过程转化为稳定运行与加反向电压过渡过程的叠加，对两种状态的解析得到三相短路时双馈电机的定子电流的解析表达式，在暂态分析的基础上提出了改进的Crowbar 电路参数整定的方法，并在一台3 MW 的双馈感应电机上对理论分析进行仿真验证。仿真实验结果显示，根据本文提出的改进的Crowbar 电路能够有效抑制转子过电流，说明了这种改进的Crowbar 电路的可行性。理论分析与仿真结果对比的一致性证明了本文分析方法的正确性，为下一步研究改进Crowbar 电路在电压跌落极限下实现低电压穿越奠定了基础。

［1］ XIE Bing，FOX B，FLUNN D. Study of fault ride－through for DFIG wind turbines［C］//IEEE Intenraitonla Conference on Electric Uitlity Deregulaiton Restructuring and Power Technolclgies.Hong Kong，China，2004.

［2］ 李辉，何蓓.双馈风力发电系统的最大风能控制策略［J］.太阳能学报，2008，29(7):797－803.

［3］ 周宏林，杨耕.不同电压跌落深度下基于撬棒保护的双馈式风机短路电流特性分析［J］. 中国电机工程学报，2009，29(3):184－191.

［4］ 蒋雪冬，赵舫. 应对电网电压骤降的双馈感应风力发电机Crowbar 控制策略［J］.电网技术，2008，32(12):84－89.

［5］ 汤蕴璆. 交流电机动态分析［M］. 北京:机械工业出版社，2005:84－90.

［6］ MORREN J，SJOERD W H. Ride through of wind turbines with doubly－fed induction generator during a voltage dip［J］. IEEE Transacitons on Energy Conversion，2005，20(2):435－441.

［7］ NIIRANEN S S，ARKKIO J.Ride－through analysis of doubly fed induction wind－power generator under unsymmetrical network disturbance power systems［J］.IEEE Transacitons on Power Systems，2006，21(4):1782－1789.

［8］ 胡家兵，孙丹，贺益康. 电网电压骤降故障下双馈风力发电机建模与控制［J］.电力系统自动化，2006，30(8):21－26.

［9］ 张建华，陈星莺，刘皓明. 双馈风力发电机三相短路分析及短路器最大电阻整定［J］.电力自动化设备，2009，29(4):6－10.

［10］ 张学广，徐殿国.电网对称故障下基于active crowbar 双馈发电机控制［J］.电机与控制学报，2009，13(1):99－103.

［11］ DITTRICH A，STOVE A.Comparison of fault ride－through strategies for wind turbines with dfim generators［C］//Presented at the 11th Eur. Power Electron. Conf.，Dresden，Germany，2005:1－8.

［12］ 尹明，李庚银，周明.双馈感应风力发电机组动态模型的分析与比较［J］.电力系统自动化，2006，30(13):22－27.

［13］ 杨淑英，张兴，张崇魏.电压跌落激起的双馈型风力发电机电磁过渡过程［J］.电力系统自动化，2008，32(19):85－91.

［14］ EKANAYAKE J B，LEE H，WU Xue－guang，et al. Dynamic modeling of doubly fed induction generator wind turbines［J］.IEEE Trans.on Power Systems，2003，18:803－809.

［15］ 汤蕴璆. 交流电机动态分析［M］. 北京:机械工业出版社，2005:84－90.

［16］ 王 健. 双馈风力发电机低电压穿越控制策略研究［D］. 扬州:扬州大学，2012.