关于M-矩阵的‖A-1‖∞改进估计式
2015-01-13高美平
周 平,陈 敏,高美平
(文山学院 数学学院,云南 文山 663000)
1 基本定义、引理和符号说明
定义1[1-6]若A = (aij)∈Zn可表示为A = sI- P,其中P ≥0,s ≥ρ(P),则称A 为M-矩阵。特别地,当s = ρ(P)时,称A 为奇异M-矩阵;当s >ρ(P)时,称A 为非奇异M-矩阵。记所有n 阶非奇异M-矩阵所组成的集合为Mn。
定义2[3]设A = (aij)∈Cn×n的特征值为λ1,λ2,…,λn,令 σ(A) = {λi,i = 1,2,…n },则σ(A)叫做A 的谱;把σ(A)中模最大的,即ρ(A)= max{| λi|,i ∈N}叫做A 的谱半径。
定义3[3,4]设A=(aij)∈Rn×n,且满足以下条件:
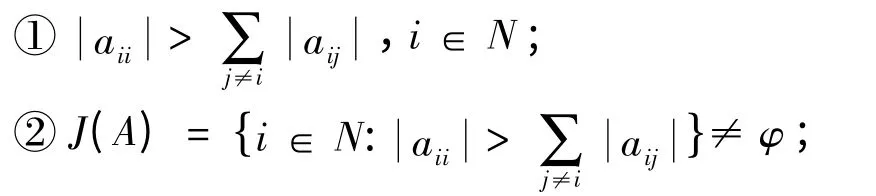
③i ∈N,i J(A),存在序列aii1,ai1i2,…,airk(i ≠i1,i1≠i2,…,ir≠k,k ∈J(A))为非零元,那么称A 是弱链对角占优矩阵。
定义4[3]设A = (aij)∈Rn×n,任取i,j ∈N,i ≠j,有aij≤0,aii>0 ,则称A 为L-矩阵。
设A = (aij)∈Zn×n,非空指标集合β(k)N,定义A[β(k)]为行数和列数都是β(k)的A 的子矩阵。
定义A(k)= A[α(k)],其中α(k)= {k +1,…n}。例如A(1)表示删去A 的第一行第一列得到的矩阵。
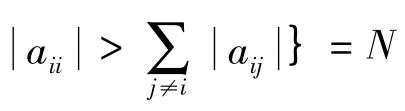
引理1[4]设A = (aij)∈Rn×n是n ×n 阶弱链对角占优M-矩阵,则B = A(1)∈R(n-1)×(n-1)也是弱链对角占优M-矩阵,且B-1= (βij)存在,βii≥0 ,(i,j = 2,3,…n)。
引理2[3,4]设A = (aij)是n × n 阶弱链对角占优M-矩阵,且A-1= (αij),则
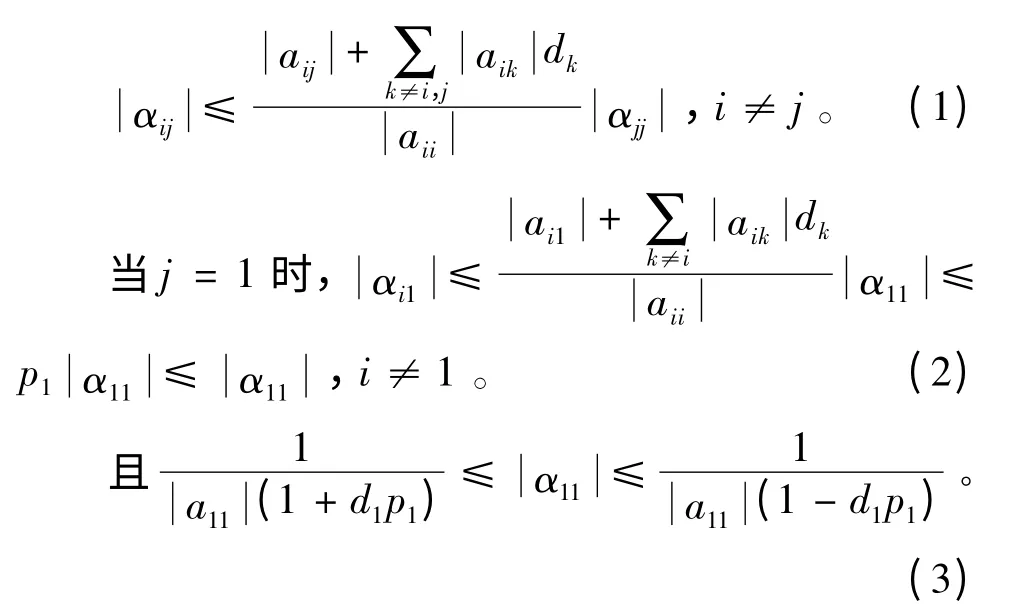
引理3[5]设A = (aij)∈Rn×n是严格对角占优M-矩阵,且A-1= (αij),则
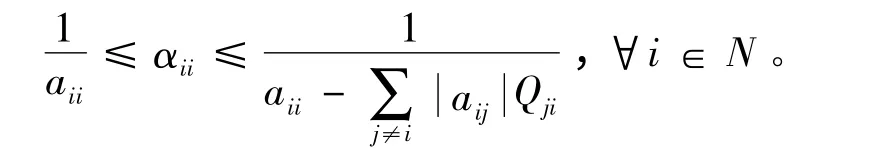
引理4[4]设A = (aij)∈Rn×n是n ×n 阶弱链对角占优M-矩阵,B = A(1)∈R(n-1)×(n-1),A-1=(αij),B-1= (βij),则
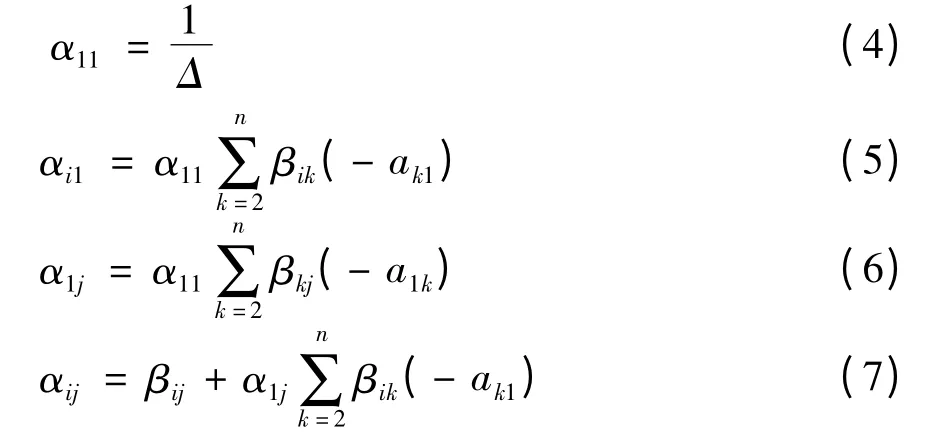
下面对文中用到的符号作以下说明:
记N = {1,2,…,n },Cn×n(Rn×n)表示所有n× n 阶复(实)矩阵构成的集合,Zn≡{A = (aij)∈Rn×n:aij≤0,i ≠j,i ∈N}。
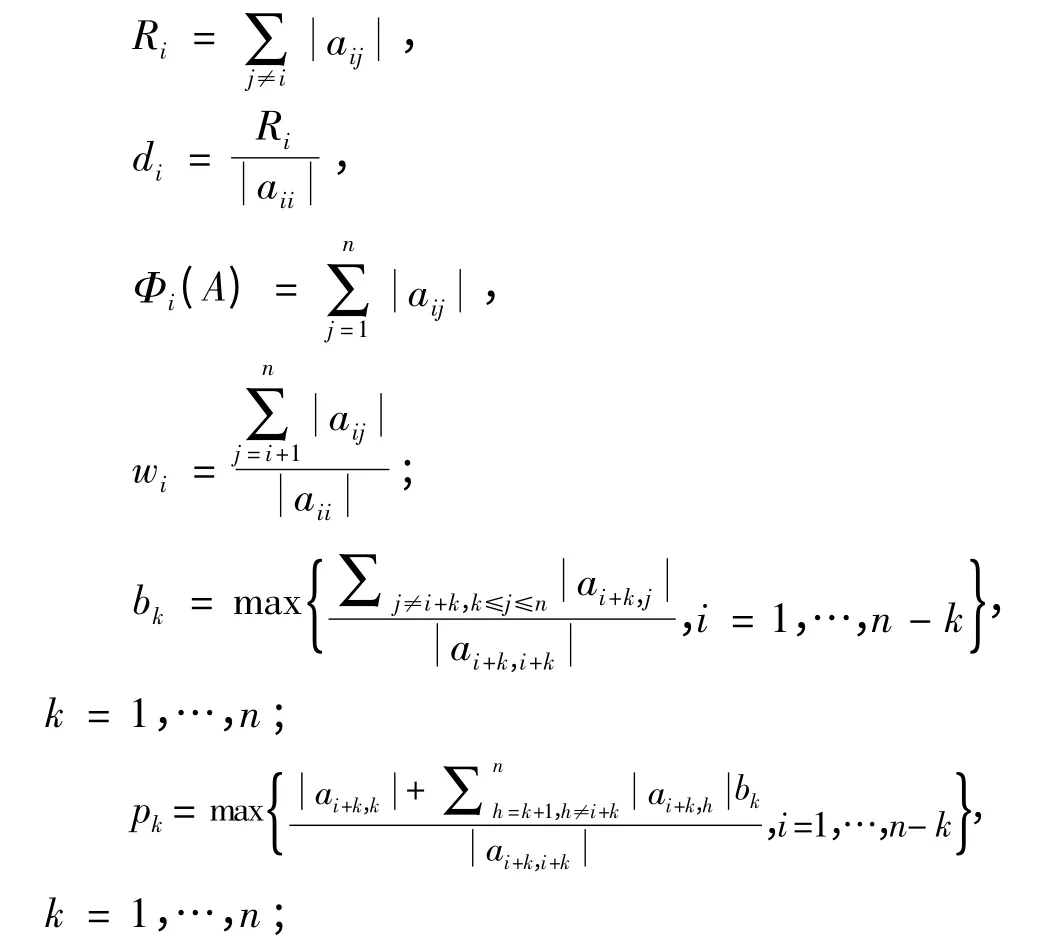
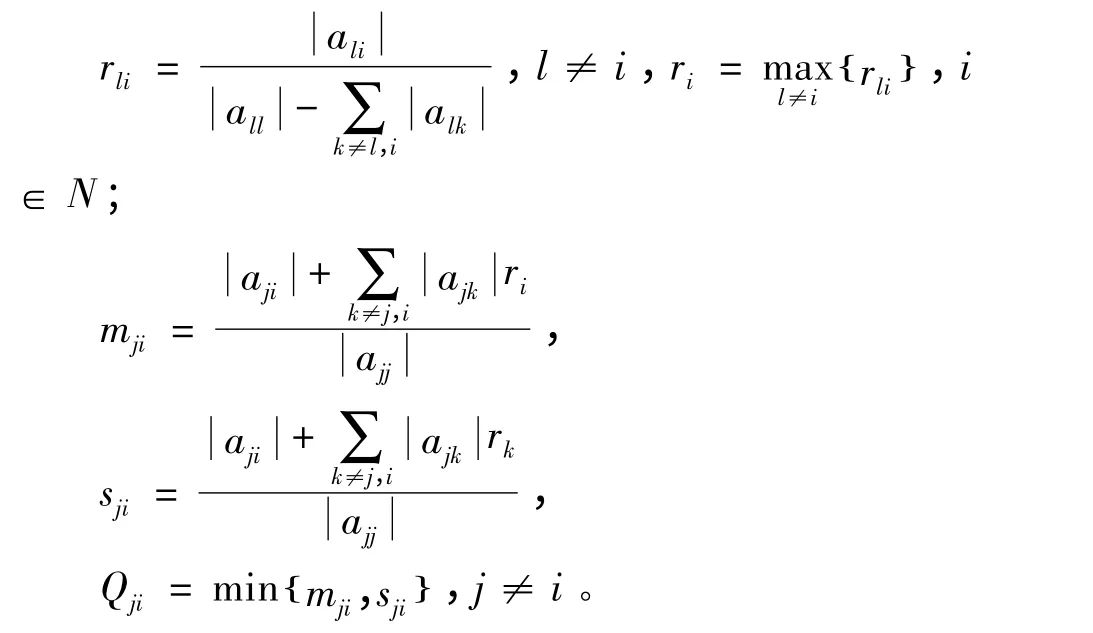
2 ‖A-1‖∞的上界和τ(A)的下界估计式
定理1 设A = (aij)∈Rn×n是严格对角占优M- 矩阵,B = A(1),A-1= (αij)∈Rn×n,B-1= (βij)∈R(n-1)×(n-1),则
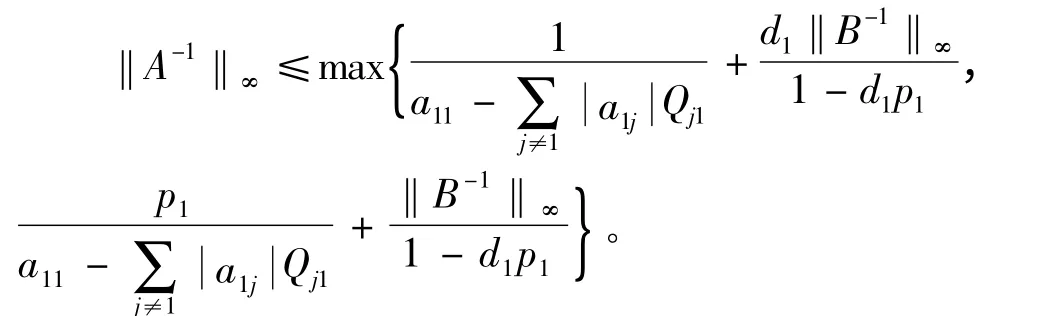
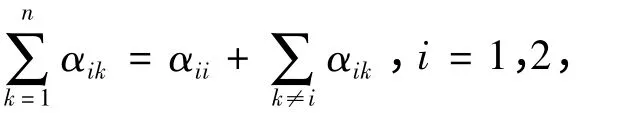
应用引理1 ,引理2 ,引理3 和(6)式,得
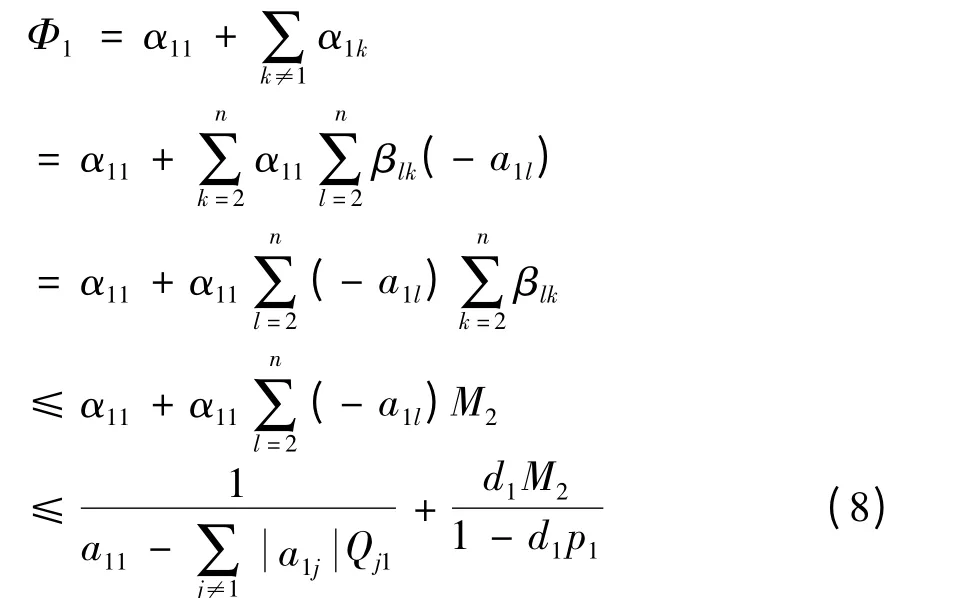
当2 ≤i ≤n 时,应用(2)式和(5)式,得
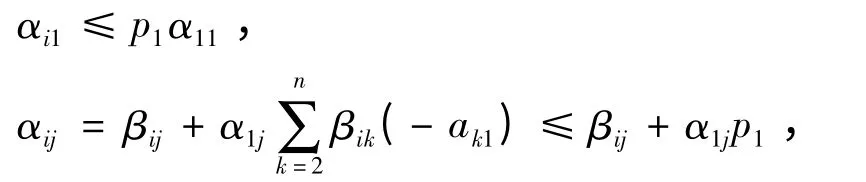
则
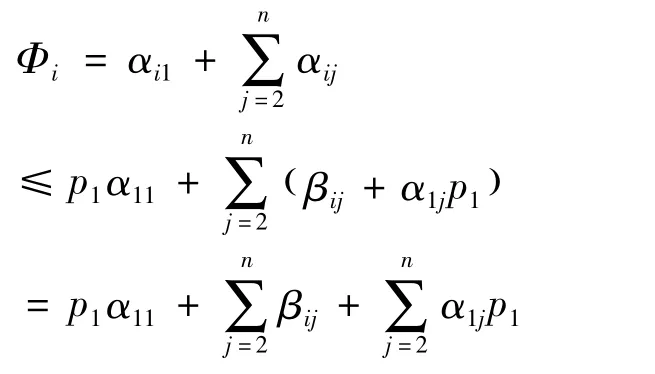
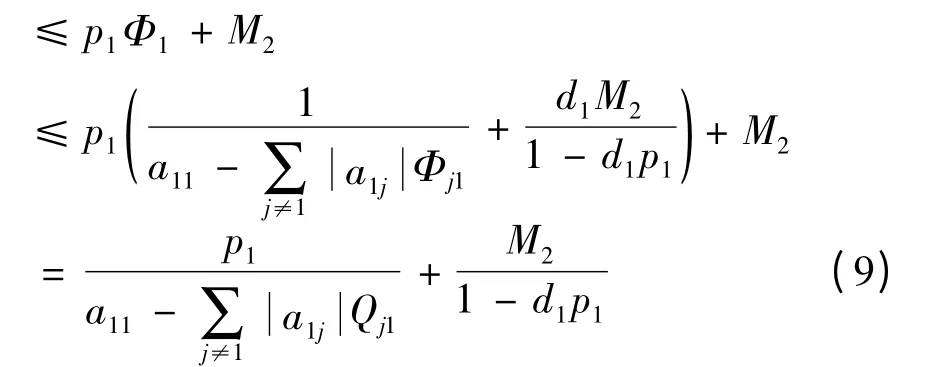
由(8)式和(9)式,得
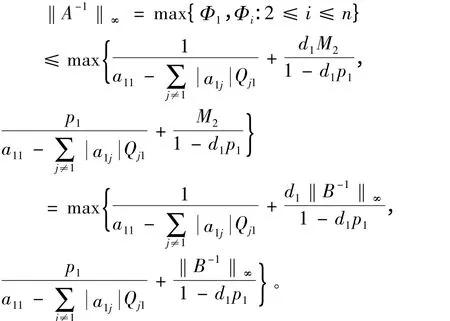
同理,根据上述定理和文献[4]中的定理1 以及A(k)的定义,应用迭代法便得到下面的结果,其中d1= w1,wn= 0 ,pn= 1 。
定理2 设A = (aij)∈Rn×n是严格对角占优M- 矩阵,则
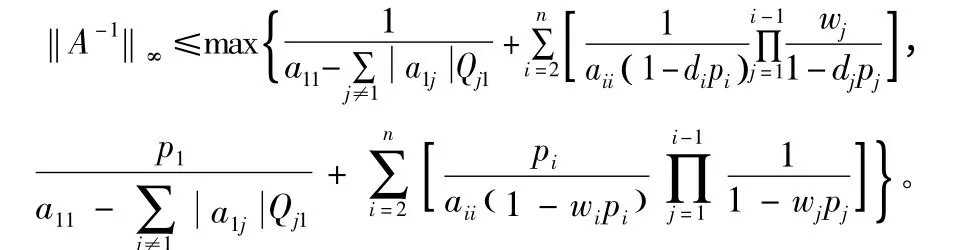
推论1 假设A = (aij)∈Rn×n是严格对角占优M-矩阵,则
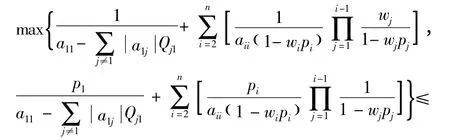
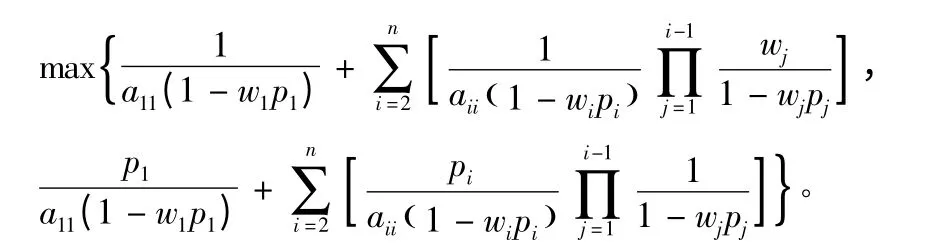
证明:根据文献[5]中引理2.6 和定理2.3 知Tj1≤p1,j ≠1,
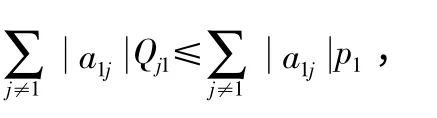
故上述结论成立。
由此推论知,本文给出的定理2 改进了文献[1,2,4]的估计式。
[1] PN Shivakumar,JJ Willians,Q Ye,et al.On two-sided bounds related to weakly diagonally dominant M-matrices with application to digital dynamics[J].SIAM J Matrix Analisis Applications,1996,17(2):298-312.
[2]王亚强,李耀堂,孙小军.An new lower bound for‖A-1‖∞of strictly diagonally dominant M-matrices[J]. 山东大学学报(理学版),2010,45(4):43-47.
[3]陈公宁. 矩阵理论与应用[M]. 北京:科学出版社,2007:53-109.
[4]TZ Huang,Y Zhu.Estimation of‖A-1‖∞for weakly chained diagonally dominant M-matrices[J].Linear Algebra and its applications,2010,432(5):670-677.
[5]FB Chen.Some new inequalities for the Hadamard product of M-matrices[J].Journal of Inequalities and Applications,2013,581(3):1186-1195.
[6]周平.M-矩阵与其逆的Hadamard 积的最小特征值下界的新估计[J]. 洛阳理工学院学报(自然科学版),2013,24(1):45-50.
