板式换热器内纳米流体单边流动与对角流动强化传热模拟

孙 斌 张冠男

(东北电力大学能源与动力工程学院)

符号说明

h——换热系数，W/(m2·K)；

K——导热系数，W/(m2·K)；

Δp——压降，kPa；

T——温度，K；

v——进口速度，m/s；

V——流量，m3/h；

φ——流体体积浓度，%；

μ——动力粘度，Pa·s；

ρ——流体密度，kg/m3；

下标：

d——对角流动；

f——基液；

m——纳米流体混合液；

n——纳米粒子；

u——单边流动；

w——纯水。

板式换热器是一种新型、高效、紧凑的热交换器，它具有传热系数高、对数平均温差大、占地面积小、质量轻、价格低廉、易清洗及易改变换热面积等优点。随着板式换热器的快速发展，其换热性能越来越高，在压力和温度不太高的换热场合中已逐步替代管壳式换热器，并广泛应用于石油、化工及制冷等领域中。

目前，对板式换热器性能的研究主要体现在提高传热效果和降低压降两个方面。Charre O等利用Fluent软件对板式换热器内部的温度场、速度场和压力场进行数值模拟[1～3]。Fernandes C S 等对板式换热器内部通道进行分析，发现改变流道的几何形状能提高换热器的传热性能[4]。梁欣等利用Fluent软件对不同尺寸的双波纹板式换热器的流场进行了模拟，经过分析对比得到换热效果最佳时双波纹板的形状[5]。Grijspeerdt K等对人字形板式换热器进行了二维和三维数值计算，最终得到优化的波纹模型[6]。张仲彬等应用数值计算软件对BR0.015F型人字形板式换热器进行数值模拟，研究了波纹倾角、高度和间距对其传热和阻力的影响，并对其单边流动和对角流动时的流动特性和换热特性进行了分析[7,8]。张毅等运用数值模拟方法和三场协同原理，对板式换热器单边流动和对角流动的流动特性和换热特性进行了分析[9]。

随着科学技术的高速发展和能源问题的日趋突出，低传热性能的换热工质已成为新一代高效传热冷却技术研究的主要障碍，而提高液体传热性能的一种有效方式是在液体中添加金属、非金属或聚合物固体粒子[10,11]。1995年Choi在国际上首次提出纳米流体的概念。目前许多学者已将纳米流体应用到工程领域。Maré T等将氧化物-水纳米流体和碳-水纳米流体应用在板式换热器中，并通过实验比较了不同纳米流体在换热器中的换热性能[12]。Tiwari A K等对不同浓度的CeO2纳米流体作为冷却剂的板式换热器进行了换热和压降性能研究，并对纳米流体的最佳体积浓度进行了测试[13,14]。Masoud H F等使用0.5%的ZnO-水纳米流体作为热流体对板式换热器进行了实验研究[15]。姚君磊研究了适用于固液两相的板式换热器的换热性能，得到了液固两相流场的流动特性与换热特性[16]。Tiwari A K等运用数值模拟方法将纳米流体用于板式换热器，发现波纹板内流体的湍流和旋涡可以提高其换热效率[17]。

笔者将纳米流体应用于板式换热器，通过数值模拟方法研究了纳米流体传热的温度、换热系数和流场的空间分布，并比较了纳米流体单边流动和对角流动时的流场特性和换热特性。

1 板式换热器模型

1.1物理模型

笔者选用BRQ035-20型人字形板式换热器，其特征参数如下：

板片材料 316L不锈钢

比热容 502J/(kg·K)

密度 7 930kg/m3

外形尺寸 258mm×100mm

试件片数 20

单片换热面积 0.015m2

有效换热面积 0.015m2×20

板片厚度 0.4mm

板间距 2mm

当量直径 4mm

角孔直径 20mm

波纹角度 120°

波纹深度 2mm

图1为冷热流体单边逆向和对角逆向流动模型，其中，前侧流道为热流体，后侧流道为冷流体。

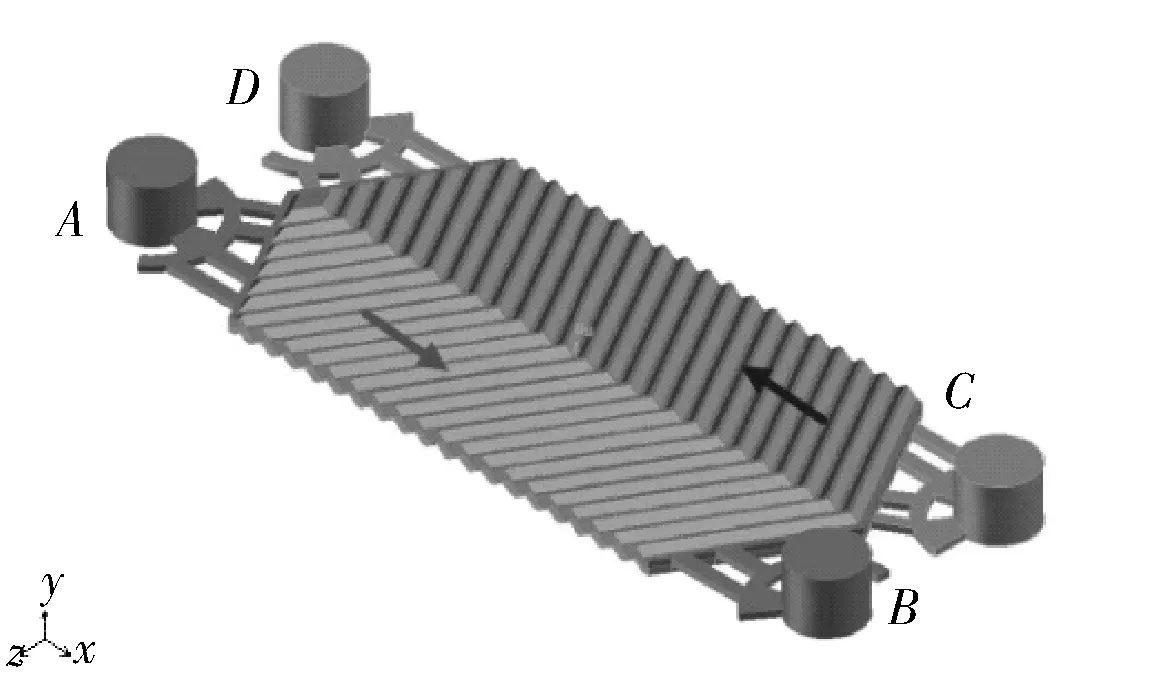
a. 单边逆向

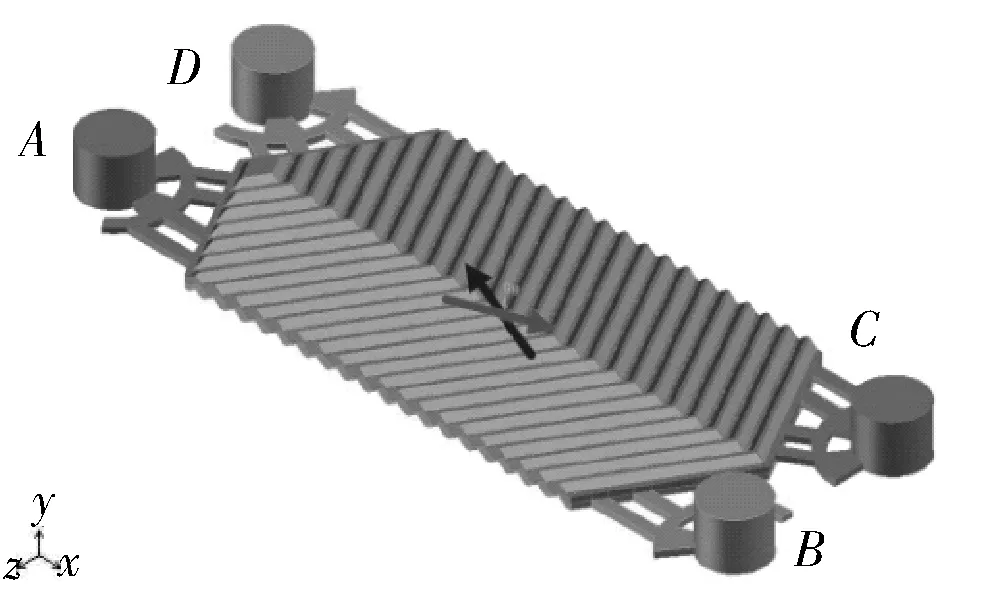
b. 对角逆向

1.2网格划分

笔者通过Pro/E3.0软件建立板式换热器冷热双流道模型，并利用Gambit软件对其进行网格划分。因波纹板式换热器内部结构复杂，故不同流动区域选择不同的网格结构和步长。首先将模型按照进出口、分流区和波纹换热区划分成10个部分，然后各自填充网格，并梯次加密网格(图2)。

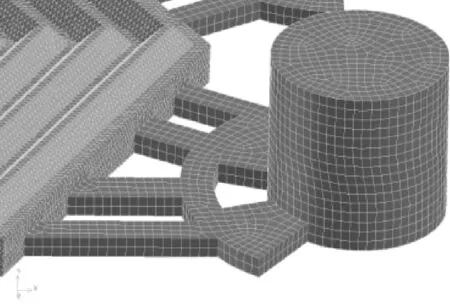
图2 板式换热器双流道网格划分

计算之前需对模型进行网格无关性验证。当波纹换热区域网格步长达到0.65 mm、网格数量增加到167万后，继续增加网格数量对模拟计算结果影响较小，因此在保证模拟准确性的基础上，笔者选用167万的网格数量进行计算。

1.3纳米流体热物性与边界条件确定

纳米流体密度ρm的计算式为：

ρm=(1-φ)ρf+φρn

笔者采用的纳米材料为Cu纳米颗粒，颗粒直径为50nm。纳米流体的粘度采用Brinkman提出的公式计算[18]：

纳米流体的导热系数采用Maxwell-Garnetts模型计算[19]：

进口采用速度入口，具体数值由流量计算得到，进口温度采用实验测得的数据；出口采用压力出口，具体数值由实验测量得到。换热面为冷、热流道相接触的面，其余各面设为绝热边界。计算中选用欧拉模型，采用Phase Coupled Simple算法进行稳态计算。能量方程的收敛残差为10-6，其余变量的收敛残差均为10-3。

1.4模型验证

为了验证计算模型和计算方法的准确性，笔者选用十二烷基苯磺酸钠(SDBS)作为分散剂，采用两步法配制纳米流体，然后对纳米流体在板式换热器中的换热性能进行实验研究。实验中板式换热器的结构尺寸与数值模拟的相同，实验系统图如图3所示。实验结果和模拟结果对比如图4所示。从图4可以看出：模拟计算得到的板式换热器换热系数与实验结果基本一致，其最大误差为4.78%，小于5.00%。因此该模型计算得到的结果是准确、可靠的。

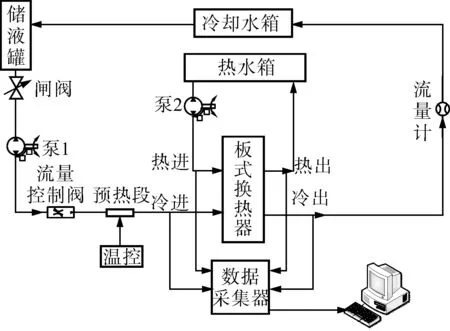
图3 实验系统结果示意图

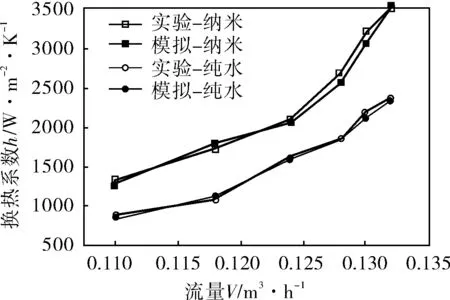
图4 实验结果与模拟结果对比

2 计算结果分析

图5为流道内温度沿x轴的分布，从图5可以看出：最高温度出现在热流体入口处，最低温度出现在冷流体入口；单边流动时温度分布较对角流动时均匀，单边流动时出口温度高于对角流动时的出口温度；4种情况下出口温度的大小关系为Tmu>Tmd>Twu>Twd，证明了纳米流体可以提高板式换热器内单边流动和对角流动的换热性能；板式换热器内纳米流体单边流动的冷侧出口温度比对角流动的冷侧出口温度高出约2℃。

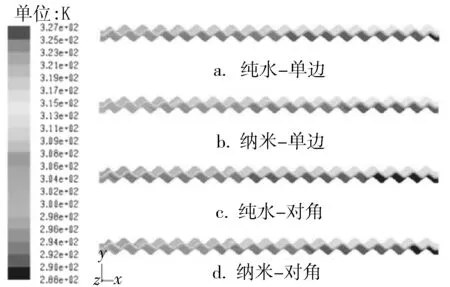
图5 流道内温度沿x轴的分布

固体的导热性能优于纯水的导热性能，在水中添加纳米粒子可以提高工质的导热性能。图6为进口速度v=0.3m/s时纯水和纳米流体单边流动和对角流动时换热系数的分布，从图6可以看出：两种流动下纳米流体的换热系数均高于纯水的换热系数；对角流动时进/出口另一侧的传热区内流速分配不均，导致换热出现死区，而单边流动则避免了这个缺点；单边流动时纳米流体的换热效率高出纯水的5.1%，同时，比纳米流体对角流动的换热系数高出95W/(m2·K)；因出口处流道发生了变化，致使流体与壁面发生碰撞，故此处换热系数较高。

图6 v=0.3m/s时纯水和纳米流体

图7为纯水和纳米流体在冷侧出口的速度矢量图。由于换热器内部较为复杂，局部区域流速过低，纯水和纳米流体在分流区和出口处的流场分布基本一致，因此冷侧出口区域的流动并不是影响纳米流体换热的主要原因。

图8为纳米流体在板式换热器内流动压降与流速的关系。由于压降与流体的密度和粘度有直接关系，而纳米流体的浓度、密度和粘度均大于纯水的，因此纳米流体的压降必然大于纯水的压降。在相同流速下，以纳米流体为冷流体的板式换热器压降大于以水为冷流体的板式换热器压降；随着流速的增大，压降增大且增大幅度变大。其中，对角流动的压降大于单边流动的压降，且均在压降允许范围内。因此在提高换热性能和降低压降方面，以纳米流体为工质的单边流动板式换热器最佳。

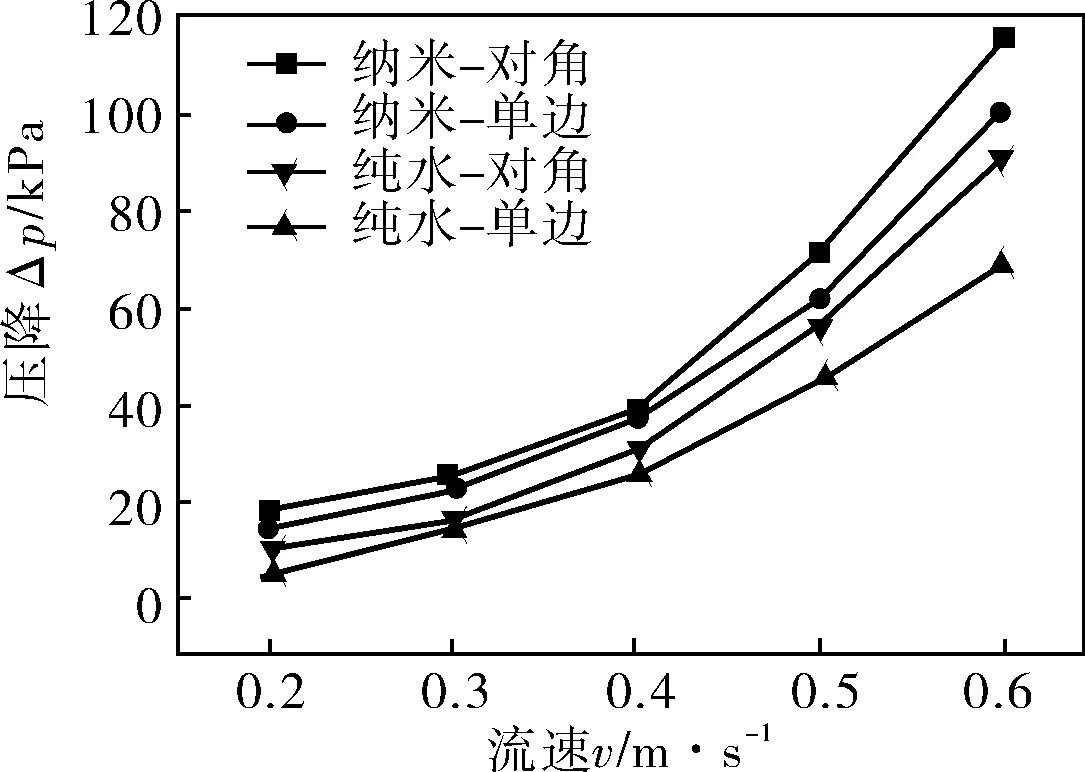
图8 纳米流体在板式换热器内流动压降与流速的关系

4 结论

4.1在模拟计算中充分考虑了纳米流体的物理性能，并通过实验验证了笔者所建立的模型是准确、可靠的。

4.2板式换热器以纳米流体为工质的单边流动和对角流动的换热效果均优于纯水的，因此纳米流体可以提高板式换热器的换热性能。

4.3纳米流体对角流动时出口温度和换热系数均高于纯水单边流动时的，但由于流道特点，其换热并不均匀，在较高流速下压降过大，而纳米流体单边流动的换热性能和降压效果最佳。

[1] Charre O, Jurkowski R, Bailly A,et al. General Model for Plate Heat Exchanger Performance Prediction[J]. Enhanc Heat Transfer, 2002, 9(5/6): 181～186.

[2] Ciofalo M. Local Effects of Longitudinal Heat Conduction in Plate Heat Exchangers[J]. International Journal of Heat and Mass Transfer, 2007, 50(15/16): 3019～3025.

[3] 桑迪科，黄思. 螺旋折流板换热器流动与传热数值模拟[J]. 化工机械，2009，36(6)：593～595.

[4] Fernandes C S, Dias R, Nóbregaa J M, et al. Simulation of Stirred Yoghurt Processing in Plate Heat Exchangers [J]. Journal of Food Engineering, 2005, 69(3): 281～290.

[5] 梁欣，张锁龙，陈文超. 双波纹板管式换热器流场的数值模拟[J]. 化工机械，2011，38(1)：83～86.

[6] Grijspeerdt K, Hazarika B, Vucinic D. Application of Computational Fluid Dynamic to Model the Hydrodynamics of Plate Heat Exchangers for Milk Processing[J]. Journal of Food Engineering, 2003, 57(3): 237～242.

[7] 张仲彬，董鹏飞，王月明，等. 板式换热器结构优化三维数值研究分析[J].化工机械，2013，40(2)：206～210.

[8] 徐志明，王月明，张仲彬.板式换热器单边流动与对角流动数值模拟[J].热能动力工程，2011,26(6)：675～780.

[9] 张毅，董鹏飞， 孙晓燕，等. 基于场协同理论的板式换热器性能优化数值研究[J]. 化工机械，2013，40(4)：487～491.

[10] 李强，宣益民. 小通道扁管内纳米流体流动与传热特性[J]. 工程热物理学报，2004，25(2)：305～307.

[11] 李强，宣益民. 铜-水纳米流体流动与对流换热特性[J]. 中国科学，2002，32(3)：331～337.

[12] Maré T, Halelfadl S, Sow O, et al. Comparison of the Thermal Performances of Two Nanofluids at Low Temperature in a Plate Heat Exchanger[J].Experimental Thermal and Fluid Science,2011,35(8): 1535～1543.

[13] Tiwari A K, Ghosh P, Sarkar J. Heat Transfer and Pressure Drop Characteristics of CeO2/Water Nanofluid in Plate heat Exchanger [J]. Applied Thermal Engineering, 2013, 57(1/2): 24～32.

[14] Tiwari A K, Ghosh P, Sarkar J. Performance Comparison of the Plate Heat Exchanger Using Different Nanofluids [J]. Experimental Thermal and Fluid Science, 2013, 49: 141～151.

[15] Masoud H F,Reza T M, Somaye N. Numerical and Experimental Investigation of Heat Transfer of ZnO/Water Nanofluid in the Concentric Tube and Plate Heat Exchangers[J].Thermal Science,2011,15(1):183～194.

[16] 姚君磊. 适用于液固两相流的宽通道板式换热器的性能研究[D]. 南京：南京航空航天大学，2012.

[17] Tiwari A K, Ghosh P, Sarkar J,et al. Numerical Investigation on Heat Transfer and Fluid Flow in Plate Heat Exchanger Using Nanofluids [J]. International Journal of Thermal Sciences, 2014, 85: 93～103.

[18] Brinkman H C. The Viscosity of Concentrated Suspensions and Solutions [J]. Journal of Chemical Physics, 1952, 20(4): 571～581.

[19] Maxwell J C. A Treatise on Electricity and Magnetism [M]. Cambridge: Cambridge University Press, 2010:435～441.