气田集气站安全监测数据异常值识别研究
2015-01-12张子涛殷存志董彩虹
张子涛 殷存志 杨 毅 董彩虹 向 敏
1中国石油北京油气调控中心
2中亚天然气管道有限公司
气田集气站安全监测数据异常值识别研究
张子涛1殷存志2杨 毅1董彩虹1向 敏1
1中国石油北京油气调控中心
2中亚天然气管道有限公司
天然气集气站监测数据异常值的准确识别具有重要意义。借助支持向量回归机算法,建立传感器在线预测模型,利用遗传算法获取最佳SVR参数,避免过拟合问题;基于一步预测误差判断方法,通过遗传算法获取最佳惩罚因子、不敏感损失函数参数和核函数参数以保证SVR回归效果,构建集气站监测数据异常识别方法;计算回归值和监测值之间的差值,若其大于阈值,可判断该实测值为异常,用回归值代替监测值,通过中心服务器写入到现场控制执行器中,则可防止安全系统误动作。工程应用表明该方法具有良好的适用性。
集气站;安全监测数据;异常;识别
为保障气田集气站安全、高效运行,需对站内工艺运行参数及可燃气数据(如硫化氢和甲烷浓度)进行在线监测。然而由于种种原因,如传感器故障、信号干扰、电缆破坏等,参数监测值易出现异常,不能准确反映现场实际情况,由此引发集气站安全系统误关断、误报警事件,影响正常生产[1]。为提高安全控制系统的可靠性,需对监测数据异常值进行准确识别。支持向量回归机算法(SVR,Support Vector Regression)具有计算量小、存储量少且算法稳定的优点[2],在信号识别、故障诊断领域得到了广泛应用。
由于存在节流降压及阀门分隔作用,集气站内工艺监测值具有相关性不强的特性,同时硫化氢和甲烷浓度传感器布置较分散,其安全监测值也无相关性,不能作为整体进行回归计算。本文借助于支持向量回归机算法,对单个传感器建立在线预测模型,基于一步预测误差判断方法,通过遗传算法获取最佳惩罚因子、不敏感损失函数参数和核函数参数以保证SVR回归效果,从而构建集气站监测数据异常识别方法。
1 支持向量回归机算法
支持向量回归机算法由支持向量机分类算法演化而来,给定训练样本{(x1,y1),...,(xl,yl)},其决策函数为,可归结为如下凸优化问题

式中ε为不敏感损失函数参数。引入松弛变量ξ、ξ*,则上述方程变为

为解出上述方程,引入Lagrange乘子η、η*、α、α*,将其转换成对偶形式,得到对偶优化问题
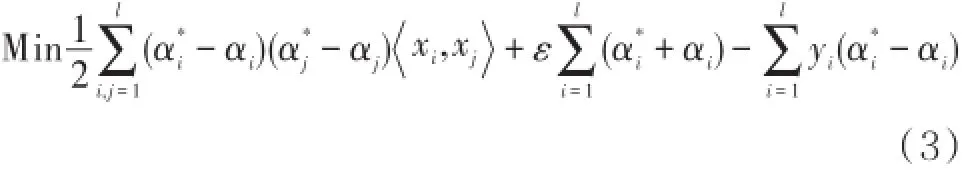
为适用于非线性问题,用核函数k(xi,xj)代替将k(xi,xj)简记为ki,j,则上述优化方程为

核函数必须满足Mercer定理,径向基核函数是较常用的核函数
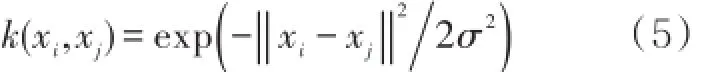
决策函数中常量b的计算方法为:若第j个输入变量对应的αj∈(0,C),则
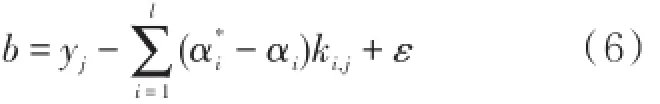
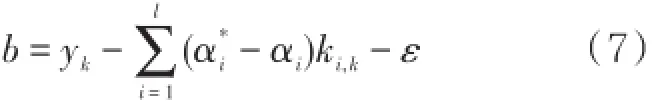
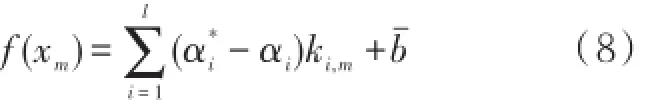
对所有样本进行遍历,计算b的均值bˉ,则回归方程为SVR的核心问题是Lagrange乘子αi和α*i的计算,一旦求出,则可构造出决策函数。将支持向量回归机转化为凸二次规划标准形式,则可以用支持向量分类机的算法进行训练。通常采用序列最小优化算法(SMO,Sequential Minimal Optimization)求解方程[3-4]。
2 集气站监测数据异常值识别方法
鉴于集气站内工艺监测值相关性不强,同时硫化氢和甲烷浓度传感器布置较分散,其安全监测值相互间也无相关性,因而其异常识别不能作为整体进行回归计算。本文采用在线一步预测法对监测数据异常进行识别。
第1步:降噪。取一组正常工况下的信号进行冗余提升小波分解[5],对各层细节信号和最后一层逼近信号进行奇异值分解降噪处理,通过重构算法获得降噪信号。
第2步:构造训练集。自然界中的任何系统都是混沌系统,气田集输系统的生产参数也不例外,具有非线性特性。本文通过相空间重构,可构造出一维时间序列的混沌吸引子。
假设信号为[s1,s2,…,sN0],运算前,须将信号归一化到[-1,1]范围内,公式为
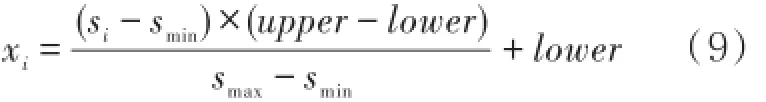
式中lower=-1,upper=1,smax和smin分别为原始信号si的最大值和最小值,xi为归一化后的值。
将归一化后的信号分为训练集[x1,x2,…,xNt]和确定集[x1,x2,…,xNc]。确定集长度,如果太长,预测出来的曲线将是一条直线;若太短,则预测精度较低。经过反复试验,Nc的取值范围为1N0≤N≤3。通过相空间重构从训练集中获得自变量和因变量,时间延迟为nt,嵌入维数一般取为1,自变量为

因变量为
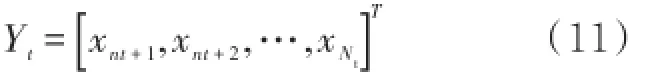
第3步:训练参数。给定SVR参数,通过SMO算法求出拉格朗日乘子及决策函数常量,构造决策函数。对自变量矩阵进行迭代更新,逐步对确定集进行预测。计算预测值和实测值间的均方差,以该均方差最小化为目标函数,通过遗传算法求解最佳延时、惩罚因子、不敏感损失函数参数和核函数参数。
第4步:构造一步预测模型。基于支持向量回归机算法,将第3步求解的最佳参数代入SVR模型进行求解。手动将拉格朗日乘子、决策函数常量、支持向量、最佳延时、惩罚因子、不敏感损失函数参数和核函数参数输入到C#程序中,构造预测模型。通过自编的OPC客户端程序,每秒从OPC服务器中读取最新数据。通过timer控件,对自变量进行在线更新,代入预测模型中对下一时刻的工艺参数进行预测,并进行逆归一化,公式为
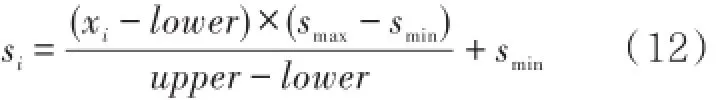
第5步:判断异常值。根据经验设置阈值,计算预测值和实测值间的相对误差,若其小于或等于阈值,则判断该监测数据为正常值;若其大于阈值,则判断该监测数据为异常值,并输出报警信息。将每个传感器的运算设为独立的线程,根据计算机性能设置最大线程数。
3 识别方法的工程应用
以普光气田301集气站压力传感器C31732.PV为例,取其某时监测信号,采样间隔为1 min,信号长度为1 440个点,此时集输系统运行工况正常。原始信号如图1所示。
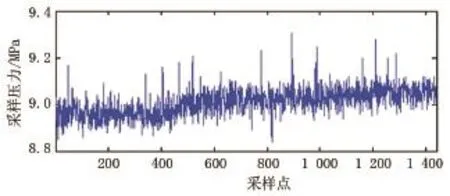
图1 压力信号
从图1可看出信号中包含很多“毛刺”,这是由噪声引起的。对信号进行3层自适应冗余提升小波分解,通过遗传算法计算出第一、二、三层细节信号和第三层逼近信号的最佳SVD降噪阶次,分别为2、2、2、6。降噪信号如图2所示,从图2可看出信号噪声明显减少,信号主体趋势较明显。从降噪信号中取出300个数作为训练样本,如图3所示。
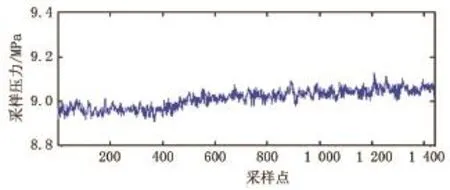
图2 降噪后的压力信号
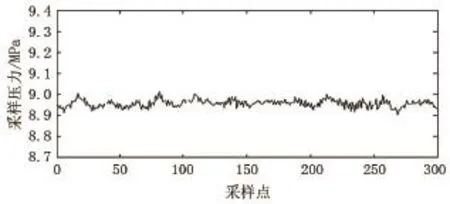
图3 训练样本
通过遗传算法获取最佳参数,自变量包括4个:嵌入维数nt、惩罚因子c、不敏感损失函数参数ε和径向基核函数参数σ,取值范围分别为1≤nt≤15、1≤c≤500、0≤ε≤1和0.2≤σ≤10,各参数运算精度分别为1、1、0.01和0.1。根据取值范围和运算精度,可算出各参数的二进制字符串长度分别为4、9、7、7。将训练样本分为训练集和确定集,训练集长度为295,确定集长度为5。训练前,将样本归一化到[-1,1]内。
离线训练在MATLAB中运行,遗传算法迭代次数为30,群体规模为300,运算时间为807 s(约14 min)。
通过训练,得到的最佳参数为:nt=9,c= 407,ε=0.349 0,σ=1.82。支持向量共30个,预测函数中的常量为-0.038 5。用于信号归一化的最大值为9.01,最小值为8.90。由以上信息可构造一步在线预测程序。为验证该预测模型精度,用一组正常数据进行验证。连续监测的9个数据为[9.05,9.06,9.09,9.02,9.04,9.06,9.12,9.10,9.07],第10个数为9.06。将前9个数代入建立的预测模型,算出预测值为8.96,相对误差为1.1%,获得了较高的预测精度。一步预测程序在MATLAB中运行,运算时间为0.039 s,远小于1 s,适合于在线运算。利用本方法,通过已有监测数据,可以准确预测下一个监测值,一旦预测值和实测值的差值大于某一阈值,则说明实测值为异常信号。下面论述如何选取合适的阈值。
原始压力信号从前到后,每次连续取9个数作为自变量代入在线预测模型,对下一个数进行预测。计算预测值与实测值间的相对误差,如图4所示。
从图4可看出大部分误差在2%以内,少部分在2%~4%之间,考虑噪声影响,设阈值为4%。在以后的在线预测中,凡是误差大于该阈值的数都是异常数据,将预测值代替实测值,以避免误关断或误报警事件的发生。
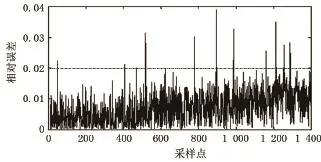
图4 一步预测相对误差
4 结论
借助于支持向量回归机算法,对集气站内每个传感器建立在线预测模型,利用遗传算法获取最佳SVR参数,避免过拟合问题;基于一步预测误差判断方法,通过遗传算法获取最佳惩罚因子、不敏感损失函数参数和核函数参数以保证SVR回归效果,构建了集气站监测数据异常识别方法。通过对正常值的预测处理,获得了判别阈值。工程应用表明,该方法具有良好的适用性。
[1]张继燕.基于实时数据库的油气处理故障诊断系统[J].油气田地面工程,2015,34(3):22-23.
[2]何正嘉,陈进,王太勇,等.机械故障诊断理论及应用[M].北京:高等教育出版社,2010:33-35.
[3]Marcos F S,Ricardo H C,Takahashic.Incipient fault detection in induction machine stator-winding using a fuzzy-Bayesian change point detection approach[J].Applied Soft Computing,2011,11(1):179-192.
[4]Saravanan N,Ramachandran K I.Incipient gear box fault diagnosis using discrete wavelet transform(DWT)for feature extraction and classification using artificial neural network(ANN)[J].Expert Systems with Applications,2010,37(1):4 168-4 181.
[5]Maurya M R,Rengaswamy R,Venkatasubramanian V.A signed directed graph and qualitative trend analysis-based framework for incipient fault diagnosis[J].Chemical Engineering Research and Design,2007,85(A10):1 407-1 422.
(栏目主持 纪嫦杰)
10.3969/j.issn.1006-6896.2015.10.001
张子涛:工程师,2003年毕业于辽宁石油化工大学自动化专业,主要从事天然气集输系统调控运行研究管理工作。
2015-06-01
18236046420、1095440060@qq.com
