A data driven approach for detection and isolation of anomalies in a group of UAVs

WangYina,*,WangDaoo,WangJianhong

aCollege of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

bCollege of Automation,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

cThe 28th Research Institute of China Electronics Technology Group Corporation,Nanjing 210007,China

A data driven approach for detection and isolation of anomalies in a group of UAVs

WangYina,*,WangDaobob,WangJianhongc

aCollege of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

bCollege of Automation,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

cThe 28th Research Institute of China Electronics Technology Group Corporation,Nanjing 210007,China

Combinatorial optimization;

Fault detection;

Gradient methods;

Model identifcation;

Unmanned aerial vehicleAbstractThe use ofgroupsofunmanned aerialvehicles(UAVs)has greatly expanded UAV’s capabilities in a variety of applications,such as surveillance,searching and mapping.As the UAVs are operated as a team,it is important to detect and isolate the occurrence of anomalous aircraft in order to avoid collisions and other risks that would affect the safety ofthe team.In this paper,we present a data-driven approach to detectand isolate abnormalaircraftwithin a team offormatted fying aerial vehicles,which removes the requirements for the prior knowledge ofthe underlying dynamic model in conventional model-based fault detection algorithms.Based on the assumption that normal behaviored UAVs should share similar(dynamic)model parameters,we propose to frstly identify the model parameters for each aircraft of the team based on a sequence of input and output data pairs,and this is achieved by a novel sparse optimization technique.The fault states of the UAVs would be detected and isolated in the second step by identifying the change of modelparameters. Simulation results have demonstrated the effciency and fexibility of the proposed approach. ©2015 Production and hosting by Elsevier Ltd.on behalf of CSAA&BUAA.

1.Introduction

Unmanned aerialvehicles(UAVs)have received growing popularities in both military and civil applications,since they can offer a great number of advantages over the manned counterparts,such as elimination of the threat to pilot’s life and longerendurance time.The capabilities can be further extended when a group of UAVs are deployed,which allows for completing tasks that cannot be achieved by a single vehicle.Hence,UAVs formation and coordination becomes an active area of research in recent years.Despite the high redundancy designs ofthe aircraft system,both hardware and software faults can also happen due to the complexity of the system and unpredicted application environment.Hence,early detection and localization of the occurrence of the anomalies is important to ensure the safety and reliability of UAVs during formation fying.

Model-driven method,based on the concept of analytical redundancy,1,2is one of the most popular approaches for fault detection and isolation(FDI).The application of this type of algorithm was pioneered by Beard and his colleagues.3In thesemethods,the system errors were detected by comparing the measured outputs of the system with predicted outputs from a pre-identifed model of the system.4The analytical redundancy,also called residual,representing the difference between the actual behavior of the system and predicted outputs of a mathematical model,approaches to zero when no anomaly is detected.On the other hand,in case the residuals deviate from zeros(zero means),a subsequent process,based on the statistical test algorithms,would be carried out to determine whether(and where)a fault occurs.In practice,however,the mathematical model,representing the dynamics of the system, is unable to exactly describe the behavior of the system due to unmodeled parameters and unknown disturbances.As a result, the residuals may not be equal to zero under normal conditions,leading to false alarms and deterioration in the performance of the system.To address this issue,the system’s observers can be designed based on decoupling principles, where the outputs of the mathematic model are robust to unknown disturbance and system uncertainties while sensitive to faults.5Zhu and Feng proposed the use of a full-order observer to detect and locate the occurrence of actuator fault, where the residuals produced by this kind of observer are more robust to model uncertainties.6Unknown input observer (UIO)based approaches,frstly developed by Watanabe and Himmelblau,7is also a popular choice of observer for model based fault detection.In the proposed method,the unknown inputs of the system can be decoupled when the observer matching condition is met.This constraint,however,is too strict to be satisfed in practicalapplications.In order to loosen the observer matching condition,algebraically decomposed technique,8unscented transformation(UT),9population-based approaches,10optimization methods11,12and neural networks,13have been incorporated into the framework of UIO, which greatly improves the performance of the original method in applications.Stochastic flters11,14,15such as Kalman flter and particle flter,have been introduced to solve the fault detection and isolation problems in recent years.In these methods,the system dynamics are modeled as a stochastic process,and the residual is generated by comparing the measured output probability density function and the predicted one.

In contrast to model-driven based FDI methods,which rely on the prior knowledge about the dynamics of a system,datadriven based FDI approaches can predict and locate the occurrence of the system errors from a large number of data collected from the dynamical process.Statistical techniques, such as principle component analysis(PCA)and its extensions,16,17partial least squares(PLS)and Fisher discriminate analysis(FDA),are one of the most popular approaches for learning the patterns of a dynamic system based on historical data.In these methods,the system dynamics are usually assumed to be linear,which cannot be hold in many realworld applications.In order to deal with the nonlinearity of the dynamic system,an iterative procedure is usually applied to solving the associated nonlinear optimization problem in these methods,which may result in undesired localoptimalsolution. To address this problem,machine learning based algorithms, e.g.,support vector machines,18artifcial neural networks19and fuzzy logic,20,21are employed to deal with nonlinear system.The unmodeled system parameters and uncertainties, however,are diffcult to incorporate into these approaches. Moreover,the machine learning based methods usually require suffcient data to approximate the system’s dynamics,which may lead to under-ftting problem if only a small volume of training data is available.

The current study introduces a fast yet robustalgorithm for the detection and isolation of the anomaly aircraft within a group of formatted fying UAVs.In contrast to conventional model based approaches rely on prior knowledge about the dynamic/measurement model of the system,the proposed method is able to identify the occurrence of the system abnormalities from inputs and outputs data,which does not require the prior knowledge about the dynamics model of the aircraft. In addition,in this paper the FDI problem is formulated as multiple objectives’convex optimization problem and solved through a fast numericalscheme,which ensures the globaloptimality of the resulting solution.It should be noted that differentfrom conventionalfault detection and isolation algorithms, which try to identify the system failure for each individualaircraft,the proposed work aims to locate the abnormal behaviored aircraft within a team of formatted fying aerialvehicles.

The reminder of this paper is organized as follows.In the following section,we frstly present the necessary technical background for data-driven based fault detection method. Then,the proposed method would be described with great detail in the following section.Section 4 presents and analyzes the experimental results,which demonstrate the effciency and fexibility of the propose approach.Finally,Section 5 is dedicated to conclusions of this research and a discussion about future directions.

2.Preliminaries

2.1.Aerodynamics of rigid-body aircraft

Given an input vector x including both control and state values of an aircraft,the dynamics of the aircraft can be written as follows:

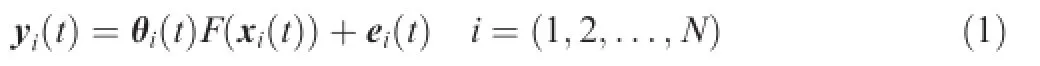
where yiis a column vector representing the measured outputs of the i th aircraft and F(·)a regression function describing the dynamics of the aircraft.To simplify the representation,we useto represent the output of the regression functionθidenotes the unknown(or partially unknown)parameters of the regression function of the i th aircraft,which is usually assumed to be full column rank.The recorded data pairsdenote the measured input–output data at each sampling time t.M is the total number of the measurements. ei(t)represents the total uncertainties and disturbances of the dynamic model,which is assumed to be independent from each vehicle within the group.To simplify the problem,we defne ei(t)as a multivariate zero mean Gaussian random vector with unknown covariance.Since ei(t)is assumed to be mutually independent,we can expect the inter-data covariance of the model uncertainties ei(t)to be zero for different aircraft:

2.2.Problem description

Assume that a group of formatted fying UAVs consists of N individual aircraft with the same structure and fight controlsystem.The dynamics of each fight,described in terms of the model parametersθi,should be similar if allof the vehicles are in normal statues.Ideally,the model parametersθishould be the same for normal aircraft,thus leading to the following condition:

whereθ0denotes the‘mean’model parameters of the aircraft system,which can be calculated by averaging the model parametersθiof each aircraft.The occurrence of the anomaly of the aircraft can be detected by fnding the change of the model parametersθi.However,due to system uncertainties and unknown disturbances,the model parametersθifor normally operated aircraft would not be exactly the same in practice.Thus,||θi-θ0||would not be zero for normal aircraft.The abnormal aircraft can be determined by fnding the value of||θi-θ0||which exceeds a pre-defned threshold. Since the model parameterθiis unable to be determined based on prior knowledge,we propose to frstly identify the model parameters,based on a sequence of inputs and outputs data pairs,for each aircraft of the team,and the abnormal vehicles are determined in the following stage by fnding the changes of parameters in the identifed model parameters.

2.3.Model parameters’estimation by maximum likelihood (ML)

Since the unknown uncertainties of the aircraft model is assumed as zero mean Gaussian distribution,the probability density function for each ei(t)can be written as

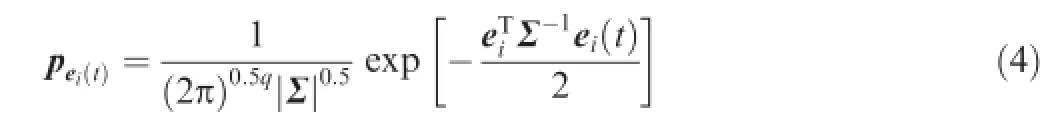
where∑is the covariance matrix of ei,which is assumed to be invertible and unknown from prior information.q represents the dimension of ei.Given a set of model parametersθi,the joint probability function of the measurement error,Pyi（t）,at all sampling time can be defned as

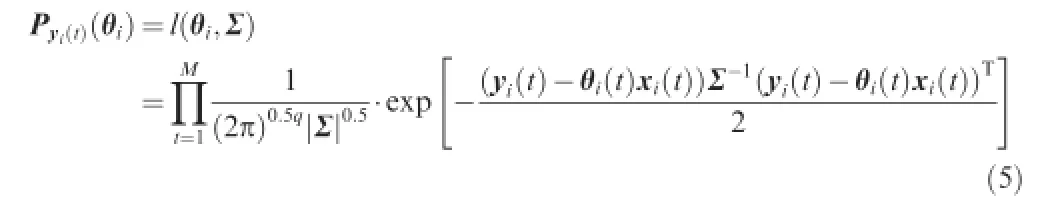
where M is the number of sampled data pairs.The joint probability function,Pyi（t）,defned in the above equation would reach its maximum when the model parametersθifully describe the actual behavior of the system.Thus,by maximizing the joint probability defned in Eq.(5),the unknown parametersθican be determined.

Maximizing the probability function in Eq.(5)is equivalent to minimizing its negative logarithm:

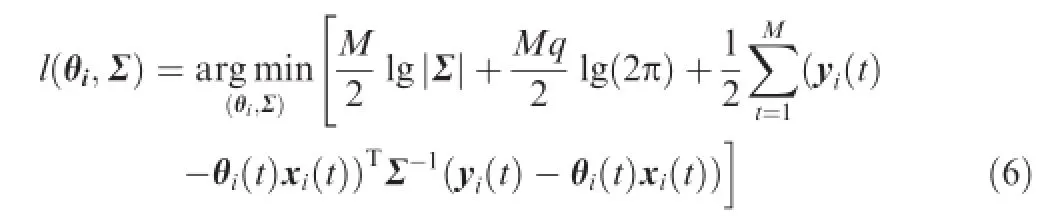
Since the covariance of the model uncertainties∑is also unknown,it should be jointly estimated from Eq.(6)and thus the minimum of Eq.(6)can be found if

According to Eqs.(6)and(7),the best estimation of the model parameters and the covariance matrix∑can be determined as

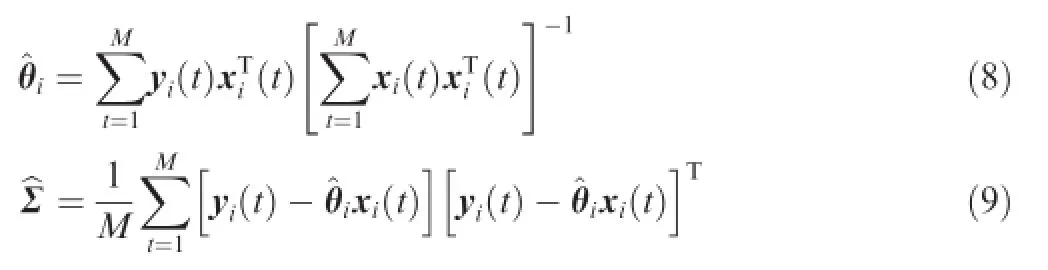
For each aircraft of the team,the modelparameters can be estimated based on Eq.(8),and the estimated mean model parameters^θ0can be therefore calculated as

If the modelparameters,i.e.,｛^θ1，^θ2，...，^θN｝,for each constitute aircraft of the team can be estimated,then,the aircraft with abnormal behavior can be determined by fnding the model parameters that deviate from the standard reference (^θ0)in terms of some distance metrics,such as Euclidian and Mahalanobis distance.12The proposed procedure for detection of the anomaly of the fight is shown in Fig.1,where the abnormal aircraft are shown within the circles.The proposed approach begins with identifying the system dynamics from a sequence of input and output data pairs,using a sparse optimization algorithm,described in Section 3.Then,an unsupervised classifer would be used to detect the abnormal aircraft, based on the model parameters estimated from the frst stage of the proposed method.

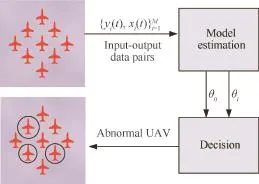
Fig.1 Proposed procedure for detecting and isolating the anomaly of UAVs.

3.Proposed method

3.1.Anomaly detection and isolation through sparse optimization

As discussed previously in Section 2.2,the model parameters estimated by using maximum likelihood(ML)based algorithms assume the model uncertainties subject to Gaussian distribution with zero means,which cannot be held in many real world applications.In this section,we present a sparse optimization based technique to estimate the model parameters based on input and output data pairs alone.Assumingthat there are r out of N aircraft encountering some system fault during formatted fying,the model parameters can be identifed by solving the following constrained optimization problem:

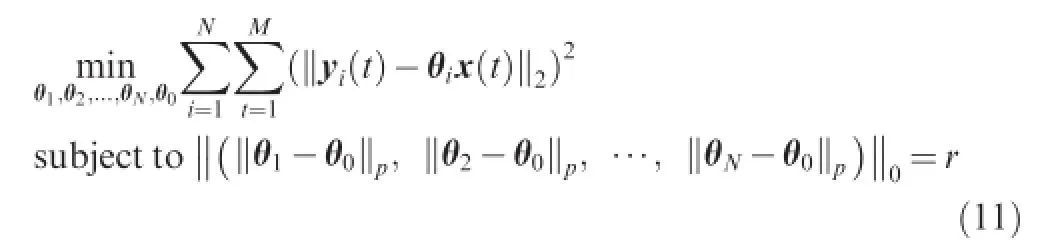
where the notion||·||pdenotes LpEuclidian norm,and L0norm is defned as the number ofnon-zero elements,indicating the number of abnormal aircraft.

According to optimal control theory,the constrained optimization problem defned in Eq.(11)can be translated to an unconstrained problem as

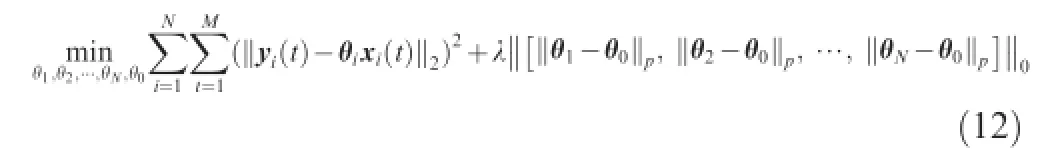
whereλis a constant and can be determined based on convex optimization technique.22By solving the optimization problem in Eq.(12),the unknown modelparameters｛^θ1，^θ2，...，^θN，^θ0｝can be determined.The optimization problem defned in Eq. (12),however,is impractical to solve.The reasons are twofolds.Firstly,the cost function defned in Eq.(12)is not convex due to the existence of the L0norm,which may cause diffculties in determining the optimal solution.Secondly,as discussed previously it is impractical for different aircraft to have the same model parameters,and thus||θi-θ0||would not be zero for normal aircraft.Yet,since we have assumed that normalbehaviored aircraft share similar dynamicalmodel parameters,the magnitude of the||θi-θ0||should be smallfor normalaircraft,while the value of||θi-θ0||would be large for abnormal aircraft.Based on this assumption,we use L1norm to replace the L0norm operator in Eq.(12),leading to the following convex cost function:

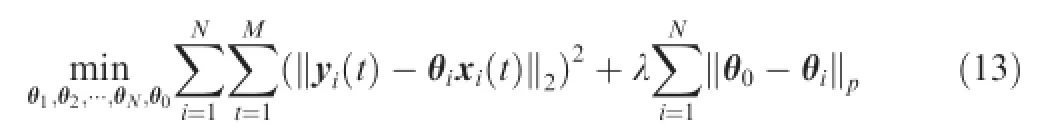
Letφdenote all of the model parameters,including the mean model parametersθ0,need to be estimated:

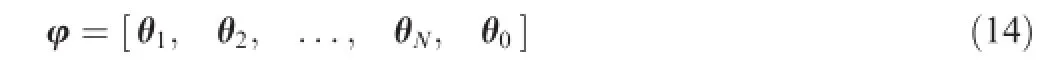
and rewrite the system’s inputs and measured outputs data as the following form:

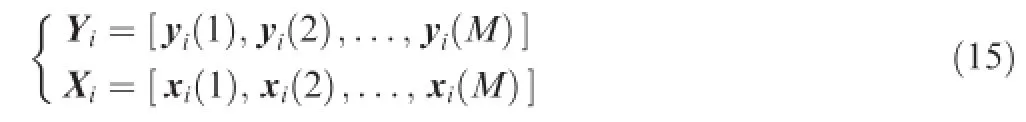
where Xiand Yiare matrix,and each column implies input vector and output vector recorded at each sampling time,respectively.Hence,Eq.(13)can be reformed,by substituting the according elements using Eqs.(14)and(15),as follows:

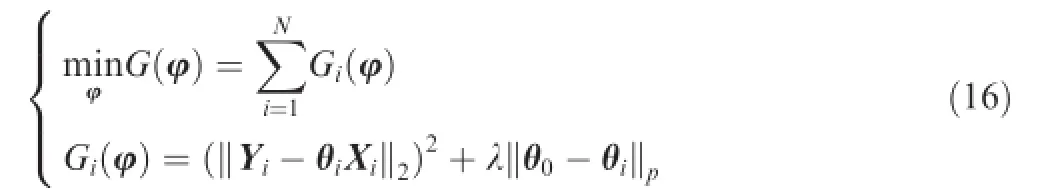
According to the necessary optimality condition of convex optimization problem,we have

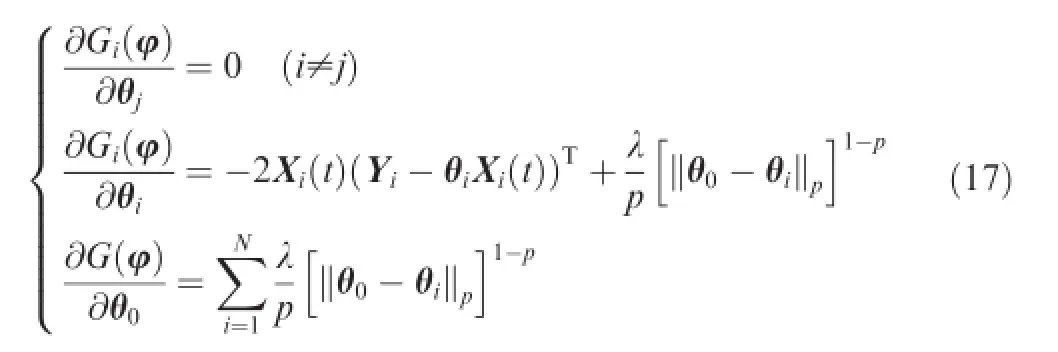
The best estimation of the unknown modelparameters can be determined as

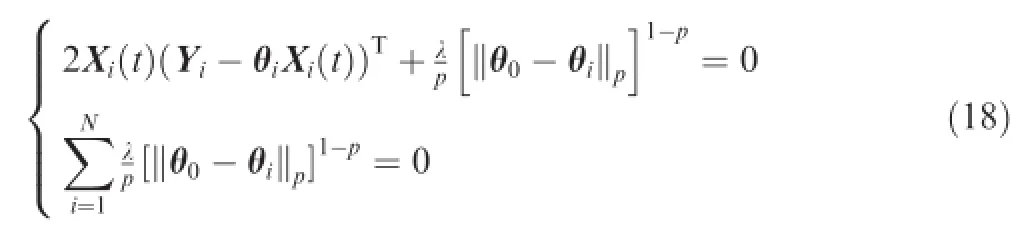
Let p=2 and Eq.(18)can be written as

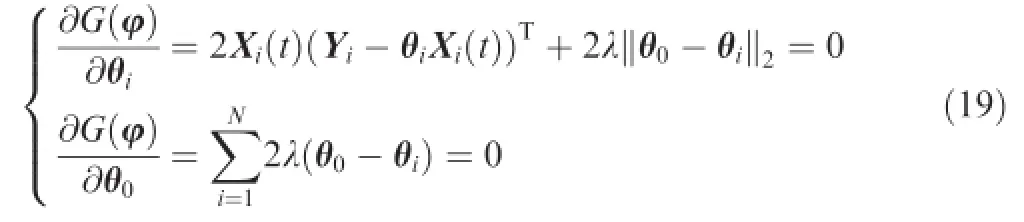
Thus,the optimalestimation of^θ0and^θican be calculated as

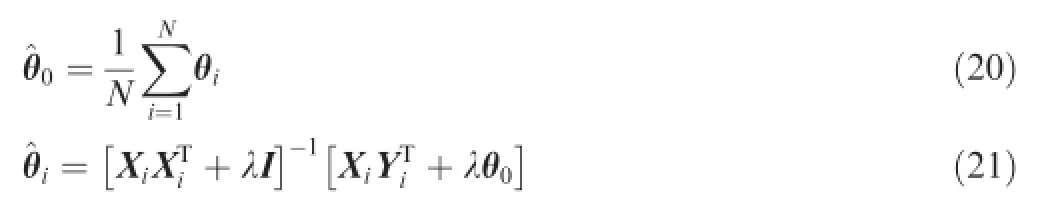
The unknown parameterθ0can be replaced by its estimation defned in Eq.(20),leading to the following solution:

By iteratively calculating^θ0and^θi,in terms of Eqs.(20)and (22),the optimal estimation of model parameters can be reached.Once the model parameters of all the aircraft have been identifed,we can detect and isolate the abnormal fight by comparing their model parameters.For each fight within the group,if its model parameters,θi,are close to the team’s mean parametersθ0,i.e.,|θi-θ0|＜ε(εis a threshold value), then it would be considered as a normal fight.In contrast,if the model parameters of the these aircraft are not consistent with the reference modelθ0,i.e.,|θi-θ0|≥ε,they would be recognized as anomaly fight.

Remark1.It should be noted thatλin Eq.(13)is also an unknown tuning parameter that can be optimized.However, since Eq.(13)is a convex function,it guarantees the global optimality of the resulting solution,despite the choice ofλ. Yet,the parameterλshould be chosen to be relatively smallin magnitude in order to prevent over-ftting of the model.

3.2.Numerical scheme

The model parameters for each aircraft cannot always be determined through Eqs.(20)and(22),since the frst element in Eq.(22)is not always invertible.To address this problem, we present an improved fast gradient numerical scheme to solve the optimization problem defned in Eq.(16).

In Eq.(16),the frst order derivative of G(φ)with respect to unknown parametersθican be calculated as

The associated Hessian matrix can be then computed as

The optimization problem defned in Eq.(30)can be solved by using the improved fast gradient method and the numerical procedure is given in Algorithm 1 as follows:

Algorithm 1.Numerical scheme of the proposed method

The eigenvalues of the Hessian matrix defned in Eq.(24), μ1andμ2,can be determined as follows:

where eigmaxand eigmindenote the maximum and minimum eigenvalues of the Hessian matrix,respectively.

In convex programming problems,μ1is a constant that satisfes Lipschitz continuity condition andμ2are convex parameters of the convex function G(φ).We defne the estimation sequence of G(φ)as

According to the properties of convex function,when γ

k→0,

Based on the concept of estimation sequence,itshould meet the following requirements:

Thus,Eq.(27)can be rewritten as

where

where hkdenotes the estimation sequence of unknown parameter matrixφ,and we assign h0to the initial estimation of the modelparameters,i.e.,h0=φ0.cirepresents the optimization coeffcient,and we assume c0satisfes the following condition:

3.3.Convergence analysis of the proposed method

In this section,the global convergence of the proposed numerical scheme for solving the convex optimization problem is analyzed.Assuming the sequence of the estimated unknown parameters is given as｛φk｝∞k=0,it should subject to the following condition:

whereλ0=1 andλk=∏k-1n=0（1-cn）,n represents the number of iteration up to k–1,when we choseγ0≥μ2,leading to the following condition.

If we letγ0=μ1and combine Eq.(31)with Eq.(32), then

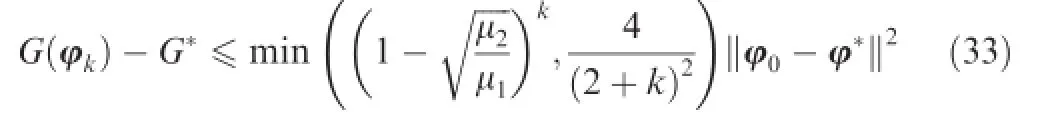
when the coeffcient c0is selected to be c0≥the estimated sequence obtained through fast gradient algorithm should satisfy the following condition:

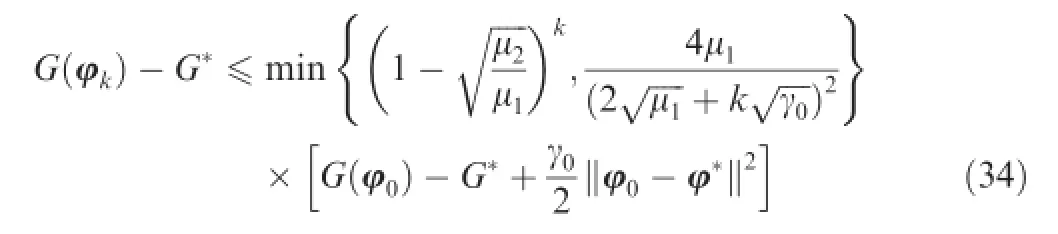
where

Since we have chosen that 1＞c0≥the frst term of the right hand side of Eq.(34)would approach to zero when the number of iteration k increases.Hence,the model parameters estimated from Algorithm 1 would converge to the global optimality of the convex function defned in Eq.(16).

4.Simulation results and analysis

In this section,we demonstrate the effciency and fexibility of the proposed anomaly detection and isolation method in terms of a series of simulation.The dynamics of the unmanned aircraft is modeled based on Beaver airframe in MATLAB,which allows for generation of inputs–outputs data pairs.The input and output vectors are defned as

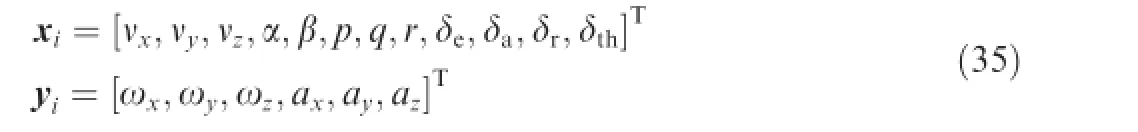
where x consists of three measured linear velocities of the aircraft along its body axes(vx,vy,vz),angle of attack（α）and slide slip(β),three angular speeds(ωx,ωy,ωz)as well as the four actuator positions,i.e.,the elevator(δe),ailerons(δa),rudders(δr)and the throttle(δth),a total number of twelve elements.The output vector y is defned by the rotationalvelocities and the three linear accelerations(ax,ay,az)along its body axes.The regression function is chosen as a linear affne function for simplify.A team of UAVs comprising of 10 identical UAVs are used throughout the experiments.

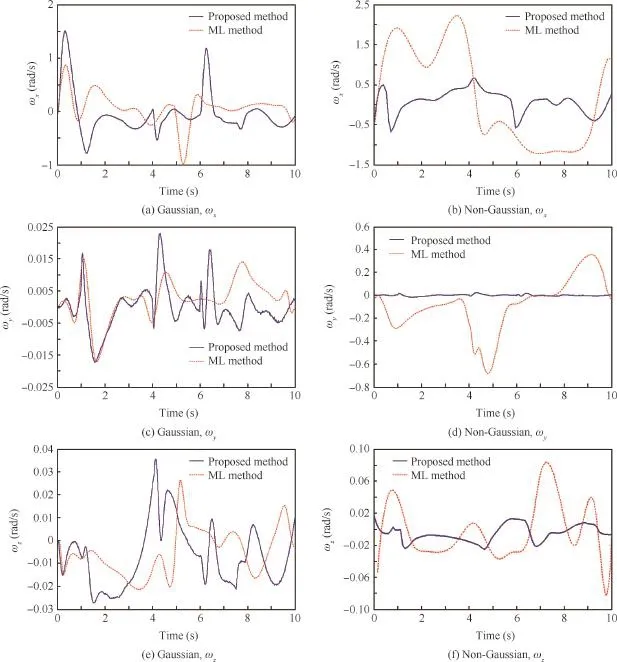
Fig.2 Diagram of model prediction error for output data with Gaussian and non-Gaussian disturbance.

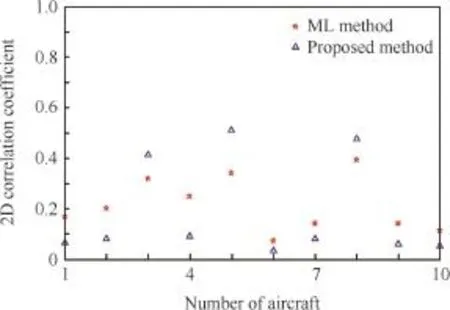
Fig.3 Inversed 2D correlation coeffcient metric between the estimated model of each aircraft and reference model.

The simulated fight path consists of three segments.The group of aircraft frstly climbs to 2000 m from their initialcursing altitude of 1500 m.Then they maintain their fight level at 2000 m for 20 s in the second segment of the planned route.In the last fight segment,these fights descend to 1500 m.The input–outputs data pairs are recorded by 10 s,with a sampling rate at 50 Hz,for each segment.Hence,for each fight segment the data contains a 500 samples in variables x and y,including 12 inputs and 6 outputs.The model parametersθiare determined based on Eq.(13)for each fight of the team,whereλ is set and fxed to 0.1 throughout the simulations.The ML based model estimation approach,described in Section 2.1,is also implemented.Both Gaussian and non-Gaussian noise(a mixed Gaussian model in this paper)are added to the measured data.

Fig.2 present the comparisons of the measured outputs and simulated outputs(based on the identifed model)errors with Gaussian and mixture Gaussian model for three output channels,i.e.,three angular velocities,respectively.It can be seen that both of the recognized models can accurately represent the dynamics of the fight given the input data with Gaussian disturbances(Fig.2(a),(c)and(e)).The proposed approach outperforms ML based method,in terms of model prediction error,in the case where unknown non-Gaussian disturbances are presented,as shown in Fig.2(b),(d)and(f).

To demonstrate the ability of the proposed scheme to detect and isolate the occurrence of abnormity in the aircraft,we randomly choose three aircraft(#3,#5 and#8)and set different types of system failures,i.e.,the non functional elevators, low engine power and angular sensory errors.To measure the similarity between identifed models,2D correlation coeffcient metric is used.It approaches to unity when two matrices are identical.Zero value of this metric,on the other hand,indicates that two matrices are entirely different.

Fig.3 depicts the inversed correlation coeffcient between the estimated model of each aircraft,the mean modelθiand the reference modelθ0.K-means algorithm23is then applied to determining the abnormal aircraft based on the correlation coeffcient metric.The classifcation results obtained through K-means algorithm is shown in Fig.4.

Fig.4(a)depicts the resulting classifcation(a team of aircraft is divided into two groups,i.e.,normal fights and abnormal fights)based on the dynamic model estimated using the proposed method,and Fig.4(b)shows the classifcation results obtained by using the dynamic model predicted by ML algorithm.It can be seen that K-means algorithm can successfully identify the abnormal behaviored aircraft using the model parameters estimated from the proposed method.On the other hand,erroneous classifcation is found when using the estimated model obtained from ML based approach(as shown in Fig.4(b)).This is due to the fact that ML based modelidentifcation methods can only deal with Gaussian noise(disturbance).In the case where the unknown noise/disturbance does not subject to Gaussian assumption,the optimality of the estimated model parameters cannot be guaranteed.Furthermore,the within-cluster sums of point to centroid distances calculated based on ML algorithm estimated model are found to be(0.0095,0.0105),which are signifcantly larger than the proposed method(0.0023,0.0049),indicating that the model parameters estimated by the proposed approach is insensitive to the unknown noise in the fight dynamics,and therefore improving the classifcation accuracy in the presence of dynamic disturbances and model uncertainties.

5.Conclusions

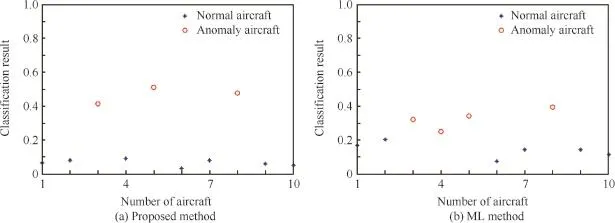
Fig.4 K-means classifcation results obtained based on correlation coeffcient calculated using different method.

In this paper,a novel two-stage algorithm is proposed to effciently detect and isolate the anomaly UAV in a formation feet.The dynamical model of each UAV is frstly identifedfrom a sequence of input–outputdata pairs using a sparse optimization based technique.An improved fast gradient based numerical scheme is developed to solve the associated optimization problem,and its convergence is analyzed.The anomalies of UAVs are determined at the second stage by fnding the changes of the model parameters,using K-means algorithm.Comparative studies have demonstrated the effciency and fexibility of the proposed approach.In terms of future research,we intend to develop an on-line scheme to estimate the dynamics of the aircraft,which would further improve the applicability of the proposed algorithm in real-world applications.

Acknowledgment

This research was supported by Fundamental Research Funds for Central Universities of China(No.NS2014090).

1.Venkatasubramanian V,Rengaswamy R,Kavuri SN,Yin K.A review of process fault detection and diagnosis Part I:Quantitative model-based methods.Comput Chem Eng 2003;27(3):293–311.

2.Castillo I,Edgar T.Model based fault detection and diagnosis. 2008.

3.Beard RV.Failure accommodation in linear systems through selfreorganization[dissertation].Masschusetts:Masschusetts Institute Technology;1971.

4.Chi C,Zhang W,Liu X.Application of analytic redundancybased fault diagnosis of sensors to onboard maintenance system. Chin J Aeronaut 2012;25(2):236–42.

5.Chen J,Patton RJ,Zhang H.Design of unknown input observers and robust fault detection flters.Int J Control 1996;63(1):85–105.

6.Zhu F,Feng C.Full-order observer-based actuator fault detection and reduced order observer-based fault reconstruction for a class of uncertain nonlinear systems.J Process Control 2010;20(10): 1141–9.

7.Watanabe K,Himmelblau DM.Instrument fault detection in system with uncertainties.Int J Syst Sci 1982;13(2):137–58.

8.Park TG.Designing fault detection observers for linear systems with mismatched unknown inputs.J Process Control 2013;23(8): 1185–96.

9.Zarei J,Poshtan J.Design of nonlinear unknown input observer for process fault detection.Ind Eng Chem Res 2010;49(22): 11443–52.

10.Duan H,Luo Q,Shi Y.Hybrid particle swarm optimization and genetic algorithm for multi-UAVs formation reconfguration. IEEE Comput Intell Mag 2013;8(3):16–27.

11.Erickson JW,Maybeck PS,Raquet JF.Racquet multipathadaptive GPS/INS receiver.IEEE Trans Aerosp Electron Syst 2005;41(2):645–57.

12.Lin R,Khalastchi E,Kaminka GA.Detecting anomalies in unmanned vehicles using the Mahalanobis distance.2010 IEEE internationalconference on robotics and automation;2010 May 3–7; Anchorage,AK;2010.p.3038–44.

13.Liu HM,Wang SP,Ouyang PC.Fault diagnosis in a hydraulic position servo system using RBF neuralnetwork.Chin J Aeronaut 2006;19(4):346–53.

14.Guo L,Wang H.Fault detection and diagnosis for general stochastic systems using B-spline expansions and nonlinear flters. IEEE Trans Circuits Syst 2005;52(8):1424–36.

15.Gao SL,Li R,Huang ZG.A fault-tolerance estimating method for ionosphere corrections in satellite navigation system.Chin J Aeronaut 2011;24(6):749–55.

16.Dunia R,Qin SJ.Jointdiagnosis of process and sensor faults using principal component analysis.Control Eng Pract 1998;6(4): 457–69.

17.Do VT,Chong UP.Signal model based fault detection and diagnosis for induction motors using features of vibration signalin two dimension domain.J Mech Eng 2011;27(9):665–6.

18.Fang R.Induction machine rotor diagnosis using support vector machines and rough set.Lect Notes Comput Sci 2006;4114:631–6. 19.Janik P,Lobos T.Automated classifcation of power-quality disturbances using SVM and RBF networks.IEEE Trans Power Delivery 2006;21(3):1663–9.

20.Picon A,Ghita O,Whelan PF,Iriondo PM.Fuzzy spectral and spatial feature integration for classifcation of nonferrous materials in hyperspectral data.IEEE Trans Ind Inf 2009;5(4):483–94.

21.Ribeiro RA.Fuzzy space monitoring and fault detection applications.J Decis Syst 2006;15(2–3):267–86.

22.Boyd S,Vandenberghe L.Convex optimization.Cambridge: Cambridge University Press;2004.

23.Snyder W,Bilbro G,Logenthiran A,Rajala S.Optimal thresholding––a new approach.Pattern Recogn Lett 1990;11(12):803–9.

WangYinreceived the B.S.degree in Electrical and Electronic Engineering from Nanjing University of Aeronautics and Astronautics in 2008.He received his Ph.D.degree in information engineering from City University London in 2011,and then became a lecturer in Nanjing University of Aeronautics and Astronautics.His main research interests are fight controland guidance,computer vision with aeronautical applications.

WangDaoboreceived B.S.and M.S.degrees in power engineering from Nanjing Aeronautical Institute in 1982 and 1985,respectively. Then he became a lecturer there,and now is a professor of Automation Engineering.His main research interests include unmanned aerial vehicle control,engine control and fault detection.

WangJianhongreceived PhD degree in automation engineering from Nanjing University of Aeronautics and Astronautics in 2011.He is now a post doctor within Research Institute of China Electronics Technology Group Corporation.His research interests are model identifcation and multiple agent coordination.

Received 25 July 2014;revised 27 August 2014;accepted 31 October 2014 Available online 24 December 2014

*Corresponding author.Tel.:+86 25 84892805.

E-mail address:yinwangee@nuaa.edu.cn(Y.Wang).

Peer review under responsibility of Editorial Committee of CJA.