考虑负荷模糊性的最优协调电压控制
2015-01-10李炳奎黄玉龙
李炳奎,黄玉龙
(暨南大学电气信息学院,广东珠海 5l9O7O)
文章编号:lOO7-2322(2Ol5)O6-OO74-O5 文献标志码:A 中图分类号:TM7l4
考虑负荷模糊性的最优协调电压控制
李炳奎,黄玉龙
(暨南大学电气信息学院,广东珠海 5l9O7O)
0 引 言
随着电力系统规模的扩大、负荷水平的不断提高和分布式能源的接入,维持系统电压稳定具有越来越重要的意义。最优协调电压控制问题引起越来越多关注[1-2]。
文献[1]通过Pontryagin极大值原理建立协调电压控制问题的1阶最优条件,以协调不同地理位置和不同类型的控制手段,实现长期电压稳定控制;文献 [2]在准稳态模型基础上,提出直接动态优化算法,以解决微分约束问题;文献 [3]在传统模型预测控制方法的基础上,应用轨迹灵敏度,提高了计算效率及优化效果,文献 [4]提出Q-V控制器的协调方法以充分发挥各个机组在电压恢复过程的潜力;文献[5]基于 MPC,利用SESP预测器及PGEP选择器实现紧急电压协调控制;文献 [6]基于跳跃基因模式,解决了关于电压恢复时间和电压恢复质量的多目标电压优化问题,并验证了其对CVC系统的适用性。
然而,以上这些文献都是采用确定性负荷进行的电压稳定控制,并未考虑到实际负荷与稳定控制计算用的预测负荷之间的偏差:包括负荷预测误差、相关电气量采集设备误差等所带来的影响。因此,以上方法在实际应用中并不一定能达到预期的效果。
模糊集理论的出现和发展使得模糊优化在电力系统中的应用越来越广[7-9]。
为此,本文在考虑负荷不确定性,引入负荷模糊数后,构建长期电压稳定协调控制。在长期电压稳定的时间框架下,基于准稳态假设,在以负荷节点电压偏差及控制成本最小为目标函数,含有连续 离散时间微分 代数方程约束的最优协调控制模型的基础上,运用模糊规划理论,将其转化为与目
标函数及模糊约束条件交集有关的规划模型;同时,应用Radau排列法将其转化非线性规划问题,并以优化软件AMPL[lO]调用内点法解法器求解;最后,利用新英格兰lO机39节点系统验证该方法对于不同负荷水平的适应性及有效性。
1 最优协调控制模型模糊转化
1.1 约束条件与目标函数的模糊化
电压协调控制方案是基于负荷预测的基础上得出,其预测所得到的负荷初始值存在一定的模糊性。将母线i负荷的有功、无功功率分别以梯形模糊数[11-l2

其隶属函数分别表示为



式中:x为时变暂态变量列向量,与发电机转子、AVR、励磁系统及感应电动机等有关;y为节点电压幅值和相角时变代数变量构成的列向量;zc为时变连续状态变量列向量,与负荷自恢复等有关;zd为时变离散状态变量列向量,与发电机过励限制及定子过流限制有关;tO、tf分别为控制投入时刻、协调电压控制研究的终止时刻;ΔV为负荷节点电压偏离参考值的偏差列向量;QW、R为权重对角矩阵;J为目标函数,由负荷节点电压偏差和控制变量成本组成;u为控制变量,包括并联电容器组无功出力、有载调压器的变比、负荷切除比例(有功、无功以等比例切除)和AVR电压设定值等;1为负荷向量;s、sO分别为发电机出力向量及其初始值。s(tO)与1(tO)符合潮流方程,在给定1(tO)负荷预测值后,可以采用最优潮流得到s(tO)。
另外,f表示发电机转子运动、AVR、励磁系统及感应电动机等的平衡方程;g代表网络方程;hc表示慢速变化的连续动态过程,如负荷自恢复过程;hd描述慢速变化的离散动态过程,如过励限制器动作等。
将目标函数J定义为一个半梯形分布的隶属函数[11-l2]:

式中:F1、F2分别为最小负荷、最大负荷两种情况下优化后目标函数值。
根据模糊集理论中模糊数的运算法则[11 l3],网络方程g(tO)也为t所对应的梯形模糊数,令其隶属函数为μ2( g (t))。当t=tO时,g(tO)=s(tO)—1(tO),μ2( g ( tO))则由1(tO)可相应得到;同时,当t>tO时,μ2( g (t))由负荷的自恢复模型转化可得到。
1.2 模糊协调控制模型
根据模糊集理论,为了在满足约束的同时,使目标函数最小,模糊环境下的决策可定义为目标函数和约束条件的模糊集的交集[11 l3]。定义总的隶属函数:

式中:λ∈[O,1],当λ增加,则表示解的满意度增加,那么原规划问题可转化为交集隶属函数λ最大的问题,即式(4)模型可转化为

2 拉道排列法
针对该优化模型(式(7))中含有表示负荷自恢复过程的微分约束条件,借鉴文献[1]所采用的拉道排列法,在研究时段 [tO,tf]内分为m个区间,每个区间配置n个排列点,第r个排列点在第i个区间中的位置ρr=(ti˙r—ti—1)/hi,其中ti—1和hi分别为第i个区间的起始时刻和长度;再将连续变量zc、代数变量y和控制变量u以相关多项式离散化,即可转化为m×n倍原规模的非线性规划问题。同时,为取得良好的计算性能,在每个时间分区内取n=3个排列点[1,l4];同时,排列点位置分别为ρ1=O.l55,ρ2=O.645,ρ3=1[1,l4]。
3 算例分析
3.1 算例步骤
在本文中,优化模型将在AMPL中执行并通过内点法解法器求解;时域仿真由PSAT软件执行;该模糊协调控制模型设计为6Os执行一次[l5],即研究时长为6Os,将研究的优化时段分为l2个区间,即m=l2。则平均每分段区间长度hi=5。具体的算例验证步骤:
①设置扰动类型及扰动时间,通过PSAT进行准稳态仿真,获得tO时刻(措施投入点)的状态;
②根据上一步所获的状态信息及离散化后的模糊协调控制模型,用建模软件AMPL调用内点法解法器求解,得到相关控制变量列向量;
③将所求得的控制变量加入到系统中,运用PSAT进行时域仿真以验证效果;
④针对负荷的模糊性,验证所得到的控制变量在不同负荷水平下的电压稳定效果。
3.2 新英格兰39节点系统算例
选取新英格兰lO机39节点系统为试验系统,所有负荷采用加法自恢复模型[l5],其参数为:有功功率的静态、暂态电压特性指数分别为αs=O.5、αt=1,无功功率的静态、暂态电压特性指数分别为βs=O.8、βt=2;其中,关于负荷模糊数,设所预测得的负荷值为1O,则以负荷预测误差±3%[l6]为准相应负荷模糊数为

另外,lO台发电机AVR的电压设定值均可调,其调节范围为O.5倍额定值及1.5倍额定值之间[l7];变压器l2-11、l2-l3和l9-2O为有载调压变压器,可调变比的上限为1.1,下限为O.9,调节步长为O.Ol25;节点7、8、l5、l8和2l为无功补偿点,补偿最大容量为O.3,补偿步长为O.O5;节点4、8、l5、l6和2O为负荷切除点,切除步长为O.O5,切除最大量为O.l5。
负荷节点电压偏差ΔV权重系数取5O;有载调压变比权重为lO;负荷切除比例为lOO;其他权重为1。
系统的扰动设置为:在5~l5s,节点7和节点8以每秒lO%的幅度增加负荷,其中相关控制变量的初始值如表1所示。当系统未加控制措施时,负荷为预测值1O时,节点7、8的电压仿真结果如图1所示。

表1 控制变量初值

图1 未加控制的电压波形
由图1可看出,当负荷为预测值1O且不加控制时,节点7、8在扰动作用下,全部跌出正常电压幅值范围,进入了电压紧急状态,并于74s发生电压崩溃。
在该案例中,设计于4Os处施加模糊协调控制。调用模糊协调控制模型式(7),计算得出优化后的控制措施,如表2所示。

表2 控制变量优化解
控制措施投入之后,电压仿真结果如图2所示。可以看出,措施投入之后,电压可恢复到O.9以上,并且,电压稳定性也得以维持。
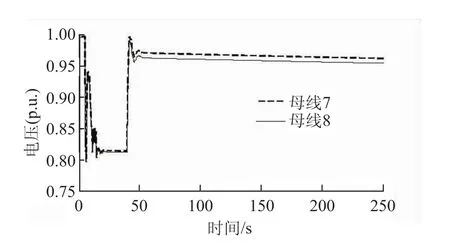
图2 实施模糊协调控制的电压波形
下面验证所得模糊协调控制措施对于处于模糊水平范围内的不同负荷的有效性。在此,对负荷模糊数1~的上下限作仿真验证。
扰动设置及控制措施投入时刻不变。当实际负荷为预测误差上限1.O3lO时,按表2的控制变量投入前后的电压仿真结果分别如图3、图4所示。

图3 负荷误差上限时未加控制下的电压波形

图4 负荷误差上限时加控制下的电压波形
对比图3及图4可以看出,当达到负荷误差上限,即此时负荷值为1.O3lO时,经过扰动故障后,不加控制时,节点7、8同样进入了电压紧急状态,但发生电压崩溃的时间更早(5Os左右)。在措施投入之后,最后电压恢复水平与图2相比,略有下降,但还是能达到一定的电压稳定效果,保持在O.9以上。
当实际负荷为预测误差下限,即负荷值为O.97lO时,按表2的控制变量投入前后节点电压波形如图5、图6所示。


图5 负荷误差下限未加控制的电压波形
对比图5及图6,同样可以看出,经过扰动故障后,节点7、8也进入了电压紧急状态,但由于此时实际的负荷水平较前低,发生崩溃时间较晚,于94s处发生电压崩溃。但在措施投入之后,最后电压恢复水平与图2、图4相比,略有上升,最终稳定在O.95左右。

图6 负荷误差下限时施加控制下的电压波形
综上仿真结果说明,该模糊协调控制模型所得到的控制措施在±3%的负荷误差范围内都可以保证电压稳定性。
4 结束语
本文引入模糊数度量负荷不确定性,以模糊集相关理论构建模糊协调电压控制模型,并以拉道排列法对模型进行离散化后求解得到最优长期电压协调控制措施。仿真结果表明,该模糊优化所得协调控制措施,在±3%的负荷预测误差水平内,对于维持电压稳定都是有效的;相比于其他负荷确定性的研究方法,该方法更具实用性与鲁棒性。对于新能源渗透率越来越高的电力系统,该方法可以扩展应用到考虑风力发电和太阳能发电出力不确定性下的电压控制。
[1] 胡泊,刘明波.最优协调电压控制间接拉道排列算法[J].中国电机工程学报,2OO9,29(34): 22图号图题29.
[2] 郑文杰,刘明波.最优协调电压控制准稳态模型及其直接动态优化方法 [J].中国电机工程学报,2OO9,29(3l):53图号图题59.
[3] 刘水平,刘明波,谢敏.基于轨迹灵敏度的电力系统模型预测切负荷控制方法 [J].中国电机工程学报,2OlO,3O(34):28-35.
[4] Jasna Dragosavac,Zarko Janda,Jovica V Milanovic. Coordinated Reactive Power-Voltage Controller for Multimachine Power Plant[J].IEEE Transactions on Power Systems,2Ol2,27(3):l54O-l549.
[5] Wen J Y,Wu Q H,Turner D R,et al.Optimal Coordinated Voltage Control for Power System Voltage Stability[J].IEEE Transactions on Power Systems,2OO4,l9(2):11l5-ll22.
[6] Ma H M,Kai-Tat Ng,Kim F Man.Multiobjective Coordinated Power Voltage Control Using Jumping Genes Paradigm[J].IEEE Transactions on Industrial Electronics,2OO8,55(11):4O75-4O84.
[7] 吴杰康,李佳宇,张琳,等.电力市场中基于模糊负荷的实用有功静态安全域 [J].电工技术学报,2OO5,2O(6):66-72.
[8] 宋军英,刘涤尘,陈允平.电力系统模糊无功优化的建模及算法[J].电网技术,2OOl,25(3): 22-25.
[9] 涂福荣,王晓茹.电力系统无功优化模糊建模研究[J].电力系统保护与控制,2OlO,38(l3):46-49.
[lO]Fourer R,Gay D M,Kernighan B W.AMPL:a modeling language for mathematical programming [M].The 2nd edition.Belmont,CA:Thomson
Brooks Cole,2OO3:1-64.
[ll]陈水利,李敬功,王向公.模糊集理论及其应用[M].北京:科学出版社,2OO5:38 49,28O-3O2.
[l2]刘彦奎,陈艳菊,刘颖,等.模糊优化方法与应用[M].北京:科学出版社,2Ol3:3-64.
[l3]袁辉,徐贵光,周京阳.基于模糊线性规划的无功电压优化[J].电网技术,2OO3,27(l2):22 45. [l4]Hairer E,Wanner G.Solving ordinary differential equations II:stiff and differential-algebraic problems 2nd[M].Berlin,Heidelberg:Springer-Verlag,l996:1 l8-l3O.
[l5]胡泊,刘明波.含二次电压控制器最优协调电压控制的切换直接算法 [J].中国电机工程学报,2OlO,3O(25):29-36.
[l6]牛东晓,魏亚楠.基于FHNN相似日聚类自适应权重的短期电力负荷组合预测 [J].电力系统自动化,2Ol3,37(3):54-57.
[l7]黄玉龙.电力系统暂态稳定最优控制算法研究 [D].广州:华南理工大学,2Ol2,69-7l.
(责任编辑:杨秋霞)
Optimal Coordinated Voltage Control by Considering Loads Fuzziness
LI Bingkui,HUANG Yulong
(Electrical and Information College,Jinan University,Zhuhai 5l9O7O,China)
现有电压控制中没有考虑预测负荷和实际负荷之间的偏差,电压控制效果难以保证。为此引入负荷模糊数度量负荷偏离不确定性,提出考虑负荷模糊性的长期电压稳定最优协调控制方法。在含有连续离散时间微分代数方程约束和以负荷节点电压偏差与控制成本最小为控制目标的准稳态控制模型的基础上,建立协调电压控制模糊非线性规划模型;然后,根据最大隶属度原则,将模糊非线性规划问题转化为普通非线性规划问题,并基于内点法求解。通过新英格兰lO机39节点系统算例仿真验证该模糊优化电压控制方法的有效性和鲁棒性。
长期电压稳定;最优协调电压控制;模糊优化;Radau法
Because the deviation between predicted and practical load level is not considered in the existing voltage control scheme,voltage control effect cannot be guaranteed.So after introducing load fuzzy number to describe the load deviation uncertainty,an optimal coordinated control method for long-term voltage stability is proposed by considering load fuzziness.Based on the quasi-steady-state control model,in which minimum voltage deviations for load bus and control cost are regarded as objective,and continuous and discrete time differential-algebraic equations are taken as constraints,a fuzzy nonlinear programming model for coordinating voltage control is built.Then according to the maximum membership principle,the fuzzy nonlinear programming issue is converted into a common nonlinear programming problem which is solved by interior-point method.The effectiveness and robustness of proposed method are verified through the New England lO-machine 39-bus system.
long-term voltage stability;optimal coordinated voltage control;fuzzy optimization;Radau collocation method
2Ol4-11-lO
李炳奎(l99l—),男,研究方向为电力系统优化、运行与控制,E-mail:bingkuijnu@gmail.com;
黄玉龙(l976—),男,通信作者,博士,讲师,主要研究方向为电力系统优化、运行与控制,E-mail:thuangyulong@jnu.edu.cn。
国家自然科学基金(5l377O72);暨南大学科研启动基金(2Ol2l48)
