供应商与零售商演化博弈系统动力学模型

蔡玲如，吴思俊，陈双

(1.汕头大学工学院，广东汕头515063；2.中国能源建设集团广东省电力设计研究院，广东广州510663)

供应商与零售商演化博弈系统动力学模型

蔡玲如1，吴思俊1，陈双2

(1.汕头大学工学院，广东汕头515063；2.中国能源建设集团广东省电力设计研究院，广东广州510663)

本文针对供应链管理中供应商与零售商之间演化博弈进行分析，讨论各种条件下演化稳定均衡的存在性，建立相应的系统动力学模型并对分析结果进行仿真验证.文章主要针对产品推广初期博弈双方不存在演化稳定均衡的情况提出了动态惩罚策略.仿真结果表明供应商采用动态惩罚策略改变了演化稳定均衡不存在的结果，并且能有效地促使零售商对产品销售采取积极态度.系统动力学为演化博弈理论在供应链管理的应用提供一个政策仿真实验平台.

供应链；演化博弈；系统动力学；动态惩罚策略

0 引言

在供应商和零售商之间如何建立良好的关系、形成有效的合约、以提高供应链整体的运作效率和效益并增强其竞争力是供应链管理中的重要的问题.博弈论作为一种对策论，已逐渐成为研究供应链管理问题的主要工具之一[1].

传统博弈论中的博弈双方“完全理性”的假设在实际应用中是难以满足的，博弈往往是一种长期的博弈，博弈双方通过在博弈过程中不停获取对方或者外界的信息不断学习，改变自己的策略.演化博弈理论突破了这种限制，将博弈参与者假设为有限理性的，具有一定的适应性学习能力[2].文献[2]应用演化博弈理论建立了单供应商和单零售商的动态监察模型并给出演化稳定策略（Evolutionary Stable Strategy，ESS）及其满足的条件[2].关于供应商和零售商行为研究除了可以建立推动式的监察模型之外，还可以从激励的角度构建拉动式的激励模型[2-5].目前所看到的大部分文献都仅仅是在静态惩罚（激励）机制的演化博弈模型上分析ESS的存在条件，没有进一步分析惩罚（激励）机制对演化博弈结果的影响.

供应链中影响供应商和零售商决策的很多因素是相互影响的，过分的简化模型很难得到有效的分析结果.随着博弈模型变量参数的不断细化，对演化博弈的定性分析就变得很困难，ESS存在条件的也难以判断和满足.文献[6]用系统动力学（System Dynamics，SD）建立了一个简单的混合战略博弈模型，仿真结果和定性分析表明其动态博弈过程存在波动性.文献[7]利用SD建立了一个双寡头博弈模型来描述两个竞争者之间的关系，其仿真结果表明模型在一定的参数变化条件下，系统会出现霍普夫分歧，系统收敛到一个有限循环，也可能出现类周期和混沌等复杂行为，并非出现常规的均衡收敛.SD为研究不完全信息条件下演化博弈的复杂动态演化过程提供了一种有效的辅助手段.

本文将演化博弈与系统动力学相结合，考虑有限理性和信息不确定的条件下，对供应商和零售商之间的一类二级供应链合作问题进行演化均衡稳定性分析，并建立相应的SD演化博弈模型以揭示供应商与零售商之间演化博弈的动态特性.

1 供应商与零售商的演化博弈模型

考虑一个供应商和一个零售商组成的委托代理关系之间的博弈问题，供应商是委托人，零售商是代理人.产品销售采用统一零售价，供应商以促销价格提供产品给零售商，零售商选择对产品采取各种促销手段来提高产品的销售量.由于单个零售商的促销手段，如广告、赠饮，可以提高产品的宣传效果，往往也能够促进其他零售商的销量，因此可能出现零售商在产品促销行为上的“搭便车”.最初采取促销手段的零售商往往由于促销费用而获得比其他零售商少的利益，最终也放弃促销.供应商无法预测到某个零售商是否会努力对产品进行促销，只能通过抽样检查的手法来判断，对消极销售的零售商采取一定的惩罚，零售商也无法预测供应商什么时候会对其进行销售方式的检查，其策略选择就是对产品进行促销销售或者不进行促销销售.

1.1.基本假设与记号

基本假设：

①供应商希望零售商能够根据具体市场情况对产品进行促销销售，提高产品知名度及其市场销售，因此供应商将部分市场推广费用作为促销让利，提供优惠的批发价格给零售商；零售商希望拿到产品的优惠批发价，从而获得产品利润最大化.

②供应商的策略选择可以是对零售商促销情况进行（检查，不检查），φ表示单位时间内零售商被抽查的概率（决策变量）；零售商从供应商进行订货销售，对产品可以采用促销销售或不采用促销销售，θ表示零售商在单位时间内采取促销销售产品的概率（决策变量）.

③以群体比例代表个体策略选择概率.模型假设演化博弈在供应商群体与零售商群体间进行，供应商每次随机与零售商群体中的个体进行博弈，供应商群体与零售商群体通过群内个体学习，采用动态复制方程来改变策略选择的比例.

④零售商在一个随机市场上销售产品，不考虑库存成本、时间延迟，并且供应商存储量足够大，可以随时满足零售商的订货需求，因此零售商的订货量与其销售量是相等的；记号：

c（0＜c＜ps）表示促销条件下供应商提供的产品优惠批发价；ps是非促销条件下供应商提供的正常批发价，p为产品零售价格，A=（ps-c）为单位产品促销费用，B=（p-ps）为零售商正常销售获益.

q表示单位时间内产品销售价格为p时，未采取任何促销措施时的市场需求.qi表示单位时间内零售商采取促销手段时的销售量增量.

Q表示零售商每次订货时的订货批量.

Cp表示零售商采取促销手段时，单位产品的促销费用.

Cs（Cs＞0）表示供应商对零售商销售情况进行检查的开销成本. P（P＞Cs）表示供应商对零售商消极销售产品采取的惩罚.

1.2.获益矩阵

假设供应商采用惩罚激励机制，则供应商与零售商之间的博弈获益矩阵如表1所示：

表1 供应商与零售商之间的博弈获益矩阵

对于零售商而言，采取促销策略的期望获益为：

采取“不促销”策略的期望获益为：

因此零售商的总体期望获益为：

对于供应商而言，采取抽查策略的期望获益为：

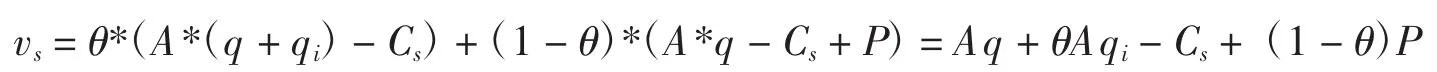
采取“不抽查”策略的期望获益为：

因此零售商的总体期望获益为：

1.3 模型求解与分析

零售商在与供应商进行博弈的同时，零售商之间并不是相互独立的.零售商的策略选择不仅仅考虑供应商的策略选择，同时还会受到其他零售商策略选择的影响.同样，供应商之间除了考虑零售商的订货情况，也会相互学习彼此的策略，取得较高的获益.考虑在两类有限理性的大群体中随机配对进行博弈的进化博弈问题.

根据生物进化复制动态的思想，采用收益较低策略的博弈方会改变自己的策略，模仿有较高收益策略的对手.采用促销策略的零售商的比例动态变化速度和供应商采取抽查策略的比例动态变化速度可以用如下的复制动态方程来表示[7-8]：

动态复制方程（3）的Jacobian矩阵为

求解：

①当Bqi-Cp＞0时，即零售商促销行为带来的产品利润获益大于促销费用，为演化博弈的ESS，即供应商不对零售商的促销情况进行抽查，零售商努力促销产品销售；

②当Bqi-Cp＜0时，即零售商促销行为的开销大于促销带来的产品销售获取的利润时，且供应商对零售商的消极销售的惩罚力度P小于促销行为带来的零售商获益损失，即P+（Bqi-Cp）＜0时，为演化博弈的ESS，即供应商对零售商的促销情况进行抽查，零售商不对产品进行任何促销行为；

③当Bqi-Cp＜0，且P+（Bqi-Cp）＞0时，为演化博弈的中心点，临界稳定，不存在ESS.故系统不存在演化稳定均衡.任何微小的变化都可能对系统的行为产生巨大影响.完全理性博弈的纳什均衡在进化博弈中并不一定是进化稳定策略[9].

2 SD博弈模型及其仿真结果

通过对供应商和零售商演化博弈模型的演化均衡的稳定性分析，得到了该博弈模型在某些条件下不存在演化稳定均衡的结论，也就是说系统不存在某一个状态使得博弈双方随着博弈次数的增加而逐渐靠近稳定.在关注系统演化均衡稳定性的同时，本文试图建立混合策略的演化博弈系统动力学模型来刻画博弈参与者之间的博弈关系的长期动力学行为趋势，为研究各种不确定因素和制定切实有效的政策提供一个仿真平台.

2.1 SD演化博弈模型

用Vensim PLE 5.6a建立供应商与零售商的演化博弈简化模型如图1所示：

图1

供应商零售商问题演化博弈的SD模型主要由四个流位、两个流率、八个中间变量和八个外部变量构成.四个流位分别用来表示供应商群体中采取抽查策略的供应商比例和不采取抽查的供应商比例，零售商群体中采取促销策略和不采取促销策略的比例；两个流率用来刻画供应商采取抽查策略的比例变化和采取促销策略的零售商比例的变化.八个外部变量分别对应表1博弈支付矩阵中的8个变量取值，如表2所示：

表2 SD模型中外部变量说明

SD模型中流率公式及其涉及到的中间变量主要是根据上一节中分析的演化博弈中的复制动力学方程（3）制定.

2.2.仿真结果

模型采用的仿真软件为vensimPLE 5.6a，假设供应商与零售商初始状态随机选择策略，双方两种策略选择比例各为50%，模型仿真参数设定为：INITIAL TIME=0，INITIAL TIME=3 000，TIME STEP=1，CHANG RATE=10，c=3，ps=4，p=5，q=300，qi=100，Cs=30.

①假设Cp=50，即Bqi-Cp＞0时，当零售商促销带来的产品销售利润大于促销费用时，无论供应商对零售商进行抽查时发现零售商没有促销行为的惩罚额度P＞（Bqi-Cp）还是P≤（Bqi-Cp），其仿真结果是一样的，仿真结果如图2，图3所示.供应商与零售商博弈演化结果是博弈双方均采取某种纯策略，供应商不对零售商进行抽查，而零售商对产品进行促销销售，结果与上一节分析一致.为演化博弈的ESS.

图2 当Bqi-Cp＞0时，供应商与零售商演化博弈结果（P＞（Bqi-Cp））

②假设Cp=50，即Bqi-Cp＞0，P=100

图3 当Bqi-Cp＞0时，供应商与零售商演化博弈结果（P＜（Bqi-Cp））

③假设Cp=150，即Bqi-Cp＜0，P=40，即P+（Bqi-Cp）＜0时，仿真结果如图4所示.供应商与零售商博弈演化结果是博弈双方均采取某种纯策略：供应商对零售商进行抽查，而零售商不对产品进行促销销售，结果与上一节分析一致.为演化博弈的ESS.

图4 当Bqi-Cp＜0，且P＜（Cp-Bqi）时，供应商与零售商演化博弈结果

④假设Cp=150，即Bqi-Cp＜0，P=100，即P+（Bqi-Cp）＞0时，零售商促销行为的开销大于促销带来的产品销售获取的利润时，但是一旦被供应商查获零售商的消极销售行为时，惩罚额度P远大于促销行为带来的零售商获益损失.当供应商抽查概率和零售商促销概率的以为初始状态时，得到如图5的仿真结果，供应商与零售商的演化博弈过程始终稳定在X5=（θ*φ*）T=（0.7 0.5）T.那么是否由此认为在Bqi-Cp＜0且P+（Bqi-Cp）＞0的条件下X5是演化稳定均衡呢？

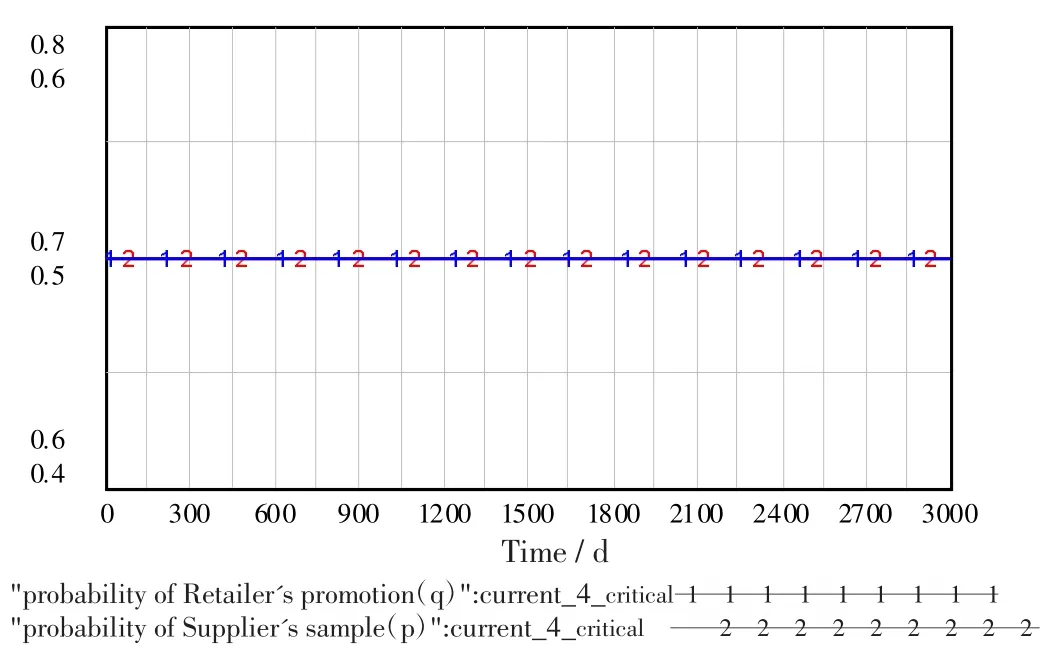
图5 当Bqi-Cp＜0，且P＞（Cp-Bqi）时演化博弈结果（θ=0.7 φ=0.5）

由分析可知X5为系统的中心点，临界稳定，也就是说任何小小的信息干扰都可能造成系统的不稳定.改变供应商与零售商的初始值，其仿真结果如图6所示.实际上，供应商为了增加产品销售量，往往会提供给零售商优惠的价格，并要求零售商对产品进行促销行为，然而产品的推广初期，促销投入的费用往往要高于短期的销售盈利，难以在短期内得到回报.在这种情况下，供应商与零售商的演化博弈结果就难以预测了.从图6可以看出，博弈双方策略选择概率都存在着波动，而且随着时间和博弈次数的增加，波动振幅逐渐增大，甚至达到最大振幅.

图6 当Bqi-Cp＜0，且P＞（Cp-Bqi）时演化博弈结果（θ=0.5 φ=0.5）

3 动态惩罚策略及其仿真结果

3.1 加大惩罚力度

最常见的控制策略就是加大惩罚力度，假设Cp=150，即Bqi-Cp＜0，Pmax=200，即Pmax+（Bqi-Cp）＞0时，得到如图7的仿真结果.也就是说单纯的增大惩罚力度，并不能从根本上改变供应商和零售商博弈过程的波动性，甚至可能由于双方选择策略选择的反复而造成合作关系的变换和中止.

图7 加倍惩罚力度供应商与零售商的动态演化过程

3.2 动态惩罚策略

在其他的应用领域里面，文献[9]提出动态惩罚策略可以稳定混合策略博弈的演化结果，使之稳定在混合策略的Nash均衡.在供应商和零售商演化博弈模型中，假设供应商对零售商采用动态的惩罚策略，也就是说供应商根据零售商群体的总体促销努力程度θ来决定对零售商的惩罚力度.假设Cp=150，即Bqi-Cp＜0，

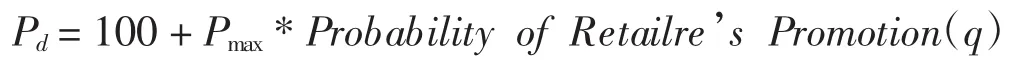
其他参数变量不变.得到如图8的仿真结果，曲线1表示零售商的演化博弈过程，曲线2表示供应商的演化博弈过程.在动态惩罚策略的影响下，演化博弈结果并不是如文献[9]中描述的稳定在混合策略的Nash均衡，而是在若干个波动后稳定在了（0，1），即是演化博弈模型的ESS稳定演化均衡.对于这样一类的二级供应链演化博弈模型中，供应商选择不对零售商的销售行为进行抽查，而零售商努力对产品的销售进行促销行为的纯策略.

图8 动态惩罚策略下供应商与零售商的动态演化过程

3.3 控制惩罚策略

假设Cp=150，即Bqi-Cp＜0，其他参数变量不变，

我们得到如图9的仿真结果，曲线1表示零售商的演化博弈过程，曲线2表示供应商的演化博弈过程.在控制惩罚策略的影响下，演化博弈结果最后同动态惩罚策略稳定在了（0，1），即是演化博弈模型的ESS稳定演化均衡，但是博弈过程中动态惩罚策略条件下出现的波动现象在控制惩罚策略条件下就得到了很好的抑制.

图9 控制惩罚策略下供应商与零售商的动态演化过程

4 结论

对于实际应用中的供应商与零售商之间这样一类两级供应链的合作博弈问题，并不是完全采用推动式的监控模型，也有拉动式的激励模型，甚至是两者结合.本文运用演化博弈和系统动力学在一系列的抽象及假设条件下建立供应商与零售商之间的合作博弈模型，系统动力学采用的数据仅仅是一种示例说明，以验证SD模型对演化博弈动态过程描述具有一定的有效性，与现实情况不可避免会存在一定的偏差.本文更主要的目的是提出了一种研究供应链博弈问题的思路，利用演化博弈分析建立供应链中的各个成员之间合作竞争关系，但是随着供应链的发展和问题研究的深入，各种不确定性因素造成了对演化博弈模型进行定性分析的困难，利用SD建立基本的演化博弈仿真模型可以考虑更多更复杂的因素对博弈结果和供应链性能的影响，同时也为供应链管理者提供了一个有效的政策仿真平台.

本文的演化博弈模型是一个推动式的监控模型，随后也将建立相应的拉动式激励模型以及推动式拉动式相结合的混合模型，分析各种策略的影响.在演化博弈的学习机制中，除了表示同类成员间学习的复制动态方程，如何在演化博弈中体现供应链中成员自身的强化学习、适应性学习等也是进一步研究的方向.

[1]Lippman S，McCardle K.The competitive news-boy[J].Operations Research，1997，45（1）：54-65.

[2]Zhou M，Deng F Q.Evolutionary dynamics of an asymmetric game between a supplier and a retailer[M]//Jiao L，Wang L，Gao X，et al.Lecture Notes in Computer Science：Advances in Natural Computation，Part II.Berlin：Springer-Verlag，2006，4222：466-469.

[3]单汩源，江黎明，吴炜炜.供应商与零售商的动态非对称演化博弈[J].商业研究，2008（07）：10-12.

[4]Chen F R.Sales-force incentives and inventory management[J].Manufacturing&Service Operations Management，2000，2（2）：186-202.

[5]黄祖庆，达庆利.基于一类两级供应链的激励机制策略研究[J].管理工程学报，2005，19（3）：28-31.

[6]Kim D H，Kim D H.A system dynamics model for a mixed-strategy game between police and driver[J].System Dynamics Review 1997，13（1）：33-52.

[7]Sice P，Mosekilde E，Moscardini A，et al.Using system dynamics to analyse interactions in duopoly competition[J].System Dynamics Review，2000，16（2）：113-133.

[8]Gintis H.Game theory evolving[M].Princeton：Princeton University Press，2000.

[9]蔡玲如，王红卫，曾伟.基于系统动力学的环境污染演化博弈问题研究[J].计算机科学，2009，36（08）：234-238+257.

[10]Wang H W，Cai L R，Zeng W.Research on the evolutionary game of environmental pollution in system dynamic model[J].Journal of Experimental Theoretical Artificial Intelligence，2011，23（1）：39-50.

A System Dynam ics M odel for Evolutionary Game Between Supp liers and Retailers

CAI Lingru，WU Sijun，CHEN Shuang
（1.College of Engineering，Shantou University，Shantou 515063，Guangdong，China；2.Institute of Electric Power Design，China Energy Construction Group，Guangzhou 510663，Guangdong，China）

In this paper,an evolutionary game between suppliers and retailers in supply chain is studied and a system dynamic（SD）model is built as simulation verification tool.The stability analysis and SD simulation result show that evolutionary equilibrium doesn’t exist under some conditions.A dynamic penalty is suggested in SD model for the equilibrium stabilization and the improvement in supply chain.Finally，the SD simulation shows that the dynamic penalty can change the evolutionary game from a critical stable state to a stable and desired state.SD provides a simulation and experiment platform for the evolutionary game theory’s development and application.

supply chain；evolutionary game；system dynamics；dynamic penalty

N 941.3

A

1001-4217（2015）01-0053-11

2014-08-25

蔡玲如（1979-），女，广东汕头人，汕头大学计算机科学与技术系副教授，博士.E-mali：lrcai@stu.edu.cn

广东省自然科学基金资助项目（S2012040007143）；汕头大学国家基金培育资助项目（NFC12003）