金星过境与和太阳系的大小

赵金荣

摘 要：金星过境是当金星与地球和太阳在一条直线上时，人们观察到的天文现象。在过去的400多年里，每次的金星过境都会让天文学家、探险家以及对天文知识感兴趣的大众感到兴奋。本文利用这样一个天文现象，说明平面三角学知识对天文学的发展所起的重要意义。

关键词：金星过境；平面三角学；直角三角形；正弦函数

David Sellers曾经说过，几乎所有的高中学生都知道太阳距地球96百万英里（或者150百万公里）。尽管这个数值与我们日常所用的尺度相比，会让人感觉巨大的无法想象，也可能因为—这类庞大的天文数据很难理解，所以被大多数受过教育的人不加思考地接受。很少人会停一下想一想怎样测量这样的一个距离。。。很少人会意识到最早对这些距离进行测量的人为之付出了什么样的努力。本文用这样的一个事例来帮助学生体会在科学上、数学上前人在测量方面曾经做过的努力，让大家体会知识不仅仅是智慧的结晶，也是汗水的浓缩。

金星过境是当金星与地球和太阳在一条直线上时，人们观察到的天文现象。在过去的400多年里，每次的金星过境都会让天文学家、探险家以及对天文知识感兴趣的大众感到兴奋。从十七世纪到二十一世纪，金星过境分别发生在1631、1639、1761、1769、1874和2004年。2012年发生的进行过境是本世纪中最后一次，在美国西部能够观察到。根据埃德蒙德。哈雷 （1656-1742）在1716年提交给皇家科学协会的一篇论文中，可以发现，探险家们到全球各地边远的地方去观察1761和1769年的金星过境。十八世纪，这些著名的探险家们和制图师们中，查尔斯。曼森和詹姆斯。库克上校在Tahiti观察到了1869年的过境现象。当观测数据进行处理时，太阳系的尺度也被确定为介于8。5和8。9角秒之间。现今的数据是8。794148角秒。

哈雷的方法用到了球面三角学的复杂工具。本文中，我们会看到一个金星过境观察和一些基础的平面三角学怎样用于求太阳系的视差，以及地球到太阳的距离。这样的课题可以让学过平面三角学知识，并对此感兴趣的学生单人或组成小组完成，小组进行会更有意思，更能让学生体会学习数学知识，并将知识用于实践的乐趣，感受团队精神。

2000多年前，埃拉托色尼计算了地球的周长大约是250，000stade（古希腊罗马的）赛跑场（长607英尺）。Stade的精确长度人们无法得知，估计大约是160米，由此给出地球周长大约是40，000公里。

练习2 设地球周长是40，000公里，证明地球的半径大约是6400公里。（现代的数据是6371公里。）

练习3 在1761年和1769年的观察数据被分析过后，太阳视差的最佳近似值是大约8。7角秒。设 是8。7角秒，使用公式（ⅰ）求地球到太阳的距离。（不要忘记把8。7角秒转换成度数。）这个计算值与现代数据149，600，000公里比较结果如何？

金星过境是指地球、金星和太阳位于同一条直线上时发生的现象。原因是因為两颗行星位于与太阳在内的同一个平面内，这样的景象非常少见，因为金星的轨道平面相对于地球的轨道平面，形成了3。4度的倾斜度。见图B。只有当三个天体沿如图B和图C所示的节线排成一条直线时才会发生金星过境现象。金星过境总是成对出现，大约相隔8年，每世纪大约一次。尽管地球和金星的轨道不是正圆，但在我们的讨论中，假设的运行轨道是以太阳为圆心的同心圆；做了这个假设后，三个天体的俯瞰图类似于图C。

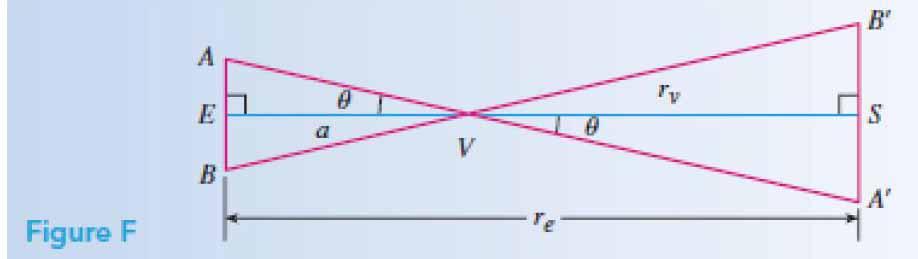
由于地球和太阳的半径与二者中心之间的距离相比都非常小，在进行计算时，需要把用于计算地球轨道半径的几何信息简化为图F中的三角图像，这里的点与图D中各点的意思相同。这个简化表示涉及到了地球和太阳的中心位置位于二者所在弦的中点处，而不是两个天体作为个体的中心。在计算过程中，误差的引入是不可避免地。

为了得到从几何学转到物理学的另一个等式。需要使用开普勒第三定律（首先发表于1616年，起初作为一个经验结果，后来使用牛顿的运动定律和引力定律推导得到）。利用假设的圆形轨道，对于两颗围绕太阳运行的行星，根据开普勒第三定律，行星运行轨道半径的比值的三次方等于轨道周期比值的平方。对于地球和金星，这里有

练习7 解方程组（ii）和（iii），比较得到的地球的轨道半径与练习3中的结果是否一致。

到此为止，利用金星过境观测数据确定地球和金星的轨道半径的工作就完成了。

这部分内容可以使用一个历史笔记总结。经过几个世纪的观测，太阳系内的六颗行星的轨道周期被叫做开普勒时间。遵循着等式（ii）的推导结果和开普勒第三定律，如果我们能发现太阳系内介于任意两颗行星之间的距离的值，那么就能够得到所有行星的轨道半径。首先测量到的行星间的距离，从地球到火星（不是到金星）是在早于本文中讨论的金星过境100多年进行的。基于1672年“火星视差”测量（以火星为顶点，以地球上相距相当远的观察位置为射线组成的角）是由巴黎的Cassini和Rocher在现在法国的Guiana进行的，Cassini确定了地球到太阳的距离是140，000，000公里。100多年后，探险家们对金星过境的观察极大地改进了这个结果。

参考文献

[1]Precalculus A Problem-Oriented Approach，Cohen，Lee，6ed，Thomson Learning，Inc。， 2005。