低氧环境下血氧序列的多尺度熵分析
2015-01-07王彬华杨军曹征涛王海涛俞梦孙
王彬华杨 军曹征涛王海涛俞梦孙
1(山东大学控制科学与工程学院 济南 250061)
2(空军航空医学研究所 北京 100142)
3(军事医学科学院卫生装备研究所 天津 300161)
低氧环境下血氧序列的多尺度熵分析
王彬华1杨 军2曹征涛2王海涛3俞梦孙2
1(山东大学控制科学与工程学院 济南 250061)
2(空军航空医学研究所 北京 100142)
3(军事医学科学院卫生装备研究所 天津 300161)
文章运用多尺度熵的方法,对低氧环境下血氧序列进行分析。研究发现,与传统的均值分析法相比,多尺度熵分析能反映机体适应低氧的动态过程;而与只在最小尺度上估计序列长度m与m+1 之间不同的样本熵相比,多尺度熵计算时间序列在多个尺度上的样本熵值,体现了时间序列在尺度上的无规则度,可以更全面的提取血氧信号的有效信息。研究结果表明,多尺度熵的血氧序列分析能对人的低氧耐力进行辨识,是一种研究机体低氧调节过程的可靠分析方法。研究还发现,多次的低氧刺激会对人体产生习服作用,机体表现出对低氧环境的记忆性。
低氧;多尺度熵;预测;记忆性
1 引 言
血氧饱和度通常用来评价人体在低氧环境下的缺氧程度,并广泛用于机体对低氧环境适应状况的监测指标[1,2]。目前对低氧环境下血氧序列的分析大都采取计算平均值的方法[3,4],此法能较好地反映机体的低氧耐受程度,但它是一静态指标,不能反映机体的低氧调节机制。
20 世纪 90 年代以来,非线性的概念和研究方法被广泛应用到生理信号的分析中,并取得了一定进展[5-9],其中比较有代表性的一类是基于熵的心率变异性分析[10-13]。熵是热力学中一种度量混乱与随机程度的测量。熵计算以其方法简单、运算快速、抗干扰能力强的优点为探测和捕捉时间序列中的有用信息提供了方便。
血氧序列是机体对低氧环境的应激反映,仅用计算平均值是远远不够的。血氧序列中蕴含了大量的内在信息,熵值则能够从一定程度上衡量这种时间前后的关联性。样本熵和基本尺度熵都是在一个最小的尺度上估计序列长度m和m+1 之间的不同,而忽略了其他尺度。我们基于多尺度熵(Multi-scale Entropy,MSE)的方法分析血氧序列信号,研究机体在低氧环境下的多尺度熵变化趋势,揭示低氧环境下不同机体的低氧适应机制。
作为开放的复杂系统的人体具有功能极强的自组织能力。机体与环境之间进行物质、能量、信息交换。当环境发生适度变化时,机体的自组织能力使机体从原来的平衡态调整到新的平衡态。而当机体经过多次低氧刺激后,机体的自组织能力使机体不断从原来的平衡态调整到新的平衡态,进而适应低氧环境,在此过程中机体表现出记性。
2 多尺度熵
多尺度熵方法首先由 Costa 等[14-16]提出,目前已经广泛应用于生理时间序列的分析。它基于样本熵,用来描述时间序列在不同时间尺度上的无规则程度。


3 低氧环境下血氧序列的 MSE 分析
3.1 实验设计
四名男性受试者(平均年龄为 22.8±2.99 岁)于实验开始前的十个月前在海拔 3800 米居住过三个月,记为 AG 组;另四名男性受试者(平均年龄 23.3±1.89 岁)在实验开始前 12 个月内未进入过海拔 1500 米以上的地区,记为 NAG 组。八名受试者的基础血氧、心率、血压无差别。
采用常压低氧舱对八名受试者进行间歇性低氧暴露,实验共进行七天,每天 150 分钟,高度为渐进型上升(3600 m、3900 m、4100 m、4300 m、4500 m、4600 m、4700 m),使用 Masimo 公司生产的 Radical-7 脉搏血氧仪对受试者进行连续血氧检测。
3.2 应用 MSE 分析血氧序列
Costa 等[19,20]认为:若熵值在尺度上单调递减,则序列在尺度上自相似性较低,结构简单,属于随机时间序列;若熵值在尺度上越大,序列自相似性大,复杂度大;若一个时间序列的熵值在绝大部分尺度上大于另一个时间序列的熵值,则说明前者要比后者复杂。基于此结论,我们对原始血氧序列(N=9000),进行=20 的多尺度熵分析。

图 1 两组受试者血氧均值比较Fig. 1 Comparison of the mean of SaO2of two groups
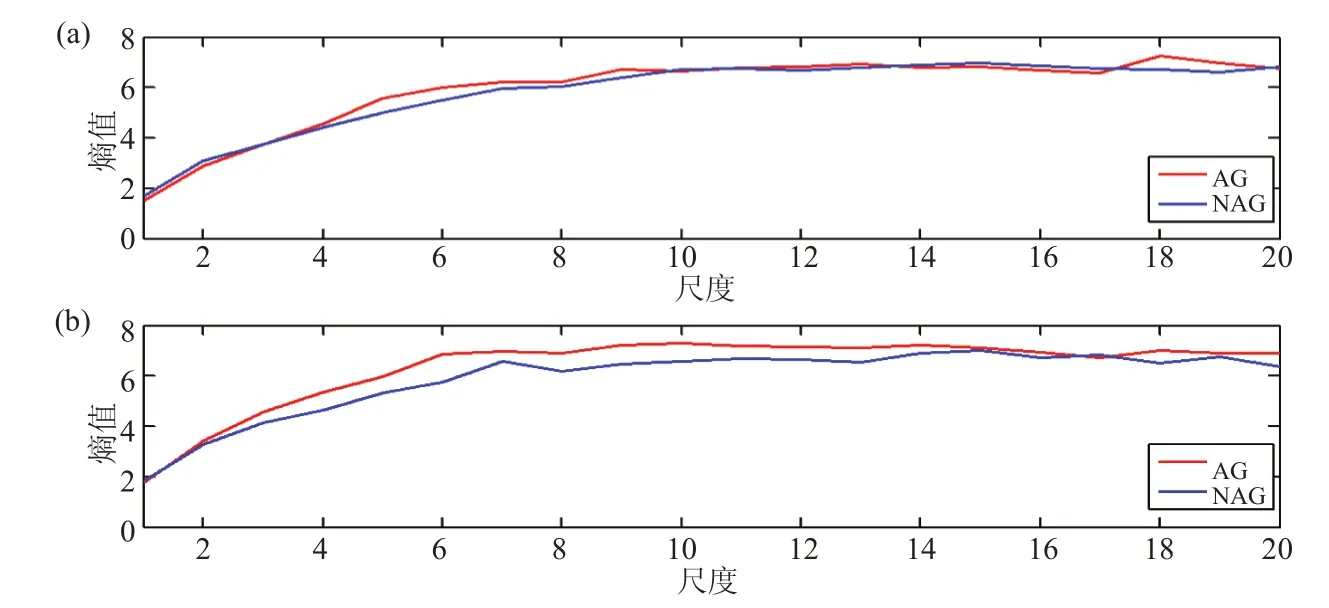
图 2 海拔高度分别为 (a) 3600 m 和 (b) 3900 m 时的血氧序列的多尺度熵分析Fig. 2 Multi-scale entropy analysis of blood oxygen sequence at (a) 3600 m and (b) 3900 m

图 3 海拔高度分别为 (a) 4100 m 和 (b) 4300 m 时的血氧序列的多尺度熵分析Fig. 3 Multi-scale entropy analysis of blood oxygen sequence at (a) 4100 m and (b) 4300 m
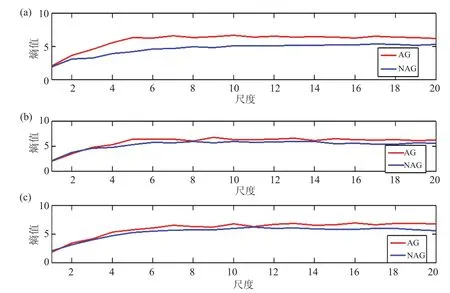
图 4 海拔高度分别为 (a) 4500 m、(b) 4600 m 和 (c) 4700 m 时的血氧序列的多尺度熵分析Fig. 4 Multi-scale entropy analysis of blood oxygen sequence at (a) 4500m, (b) 4600 m and (c) 4700 m
由图 1 可知,虽然 AG 组的血氧均值高于NAG 组,但不能反映机体的动态低氧调节机制。样本熵只是在最小尺度上估计序列长度m和m+1 之间的不同,而忽略了其他尺度,不能全面地提取有效信息。从图 2~图 4 可以看出,在模拟海拔渐进型上升阶段,AG 组与 NAG 组的样本熵(尺度=1 时)区别不大,很难达到对两组进行有效识别的目的。在海拔 3600 m、3900 m、4500 m、4600 m、4700 m 时,AG 组的血氧序列的多尺度熵曲线高于 NAG 组的血氧序列的多尺度熵曲线;海拔 4100 m、4300 m 时,AG 组的血氧序列的多尺度熵曲线低于 NAG 组的血氧序列的多尺度熵曲线。因此,采用多尺度熵可以对低氧环境下机体的低氧调节过程进行分析。
在充足的负熵流输入前提下,人对高原低氧环境的适应能力一方面表现为强大的维持自身健康的能力,另一方面,当环境氧分压下降时,只要其变化率不超过系统自适应时间常数条件,则人的各系统的功能和结构将会协同地调整到与低氧环境相适应的状态,即新环境下的健康状态。相反,如果低氧环境变化速率明显超过人体自组织时间常数时,不仅自适应时间会大大延长,甚至会使整个人体系统失去稳态,走向长期不适应状态,即慢性高原病状态。
AG 组已在海拔 3800 m 的高原居住三个月,机体通过自我调节,已逐步适应高原低氧环境。所以当 AG 组机体再次暴露在海拔 3900 m 环境时,机体能够尽量保持组织氧化作用,最大限度地运用可利用的氧气,产生尽可能多的能量来适应高原环境;而当 NAG 组第一次暴露在海拔 3900 m 的环境中,巨大的环境变化导致其需要一定的时间去适应此环境。此时 AG 组的多尺度熵值曲线高于 NAG 组的多尺度熵值曲线。在海拔 4300 m 时,AG 组本身具备一定的低氧储备,加之 3900 m 时的低氧调节,已经能完全适应一定海拔高度的高原环境,当机体暴露在 4300 m 时,不需要过多的机体调节就能适应此环境;NAG 组则需要积极调动自身的低氧调节机制,以达到适应低氧环境的目的。此阶段NAG 组的血氧多尺度熵值曲线高于 AG 组。海拔 4500 m 时的氧分压只有平原的 60%,在此阶段机体的低氧调节是一方面,更多的是对机体自身潜能的考验。此阶段,AG 组的多尺度熵值曲线高于 NAG 组的多尺度熵值曲线。
4 人体的低氧记忆性
分别计算两组受试者 MSE 曲线面积并求其均值,结果如图 5 所示。由图可知,八名受试者经过适度的低氧刺激,机体产生低氧预适应效果,提高了机体适应低氧应激的能力,达到了一个新的自稳态。另一方面,NAG 曲线近似为 AG曲线的右移结果。AG 组由于自身机体已产生一定的低氧记忆性,机体的低氧调节机制启动更快,具有更敏感的预判能力,更能适应高海拔高原环境;NAG 组没有前期的低氧储备,只能通过自身机体调节去适应低氧环境,当海拔较高,环境低氧刺激量超过机体的低氧承受能力时,机体适应低氧环境的能力会下降。因此,NAG 自稳态值低于 AG 自稳态值。两组实验对象低氧调节机制的差别,正是人体自组织低氧记忆性的体现。
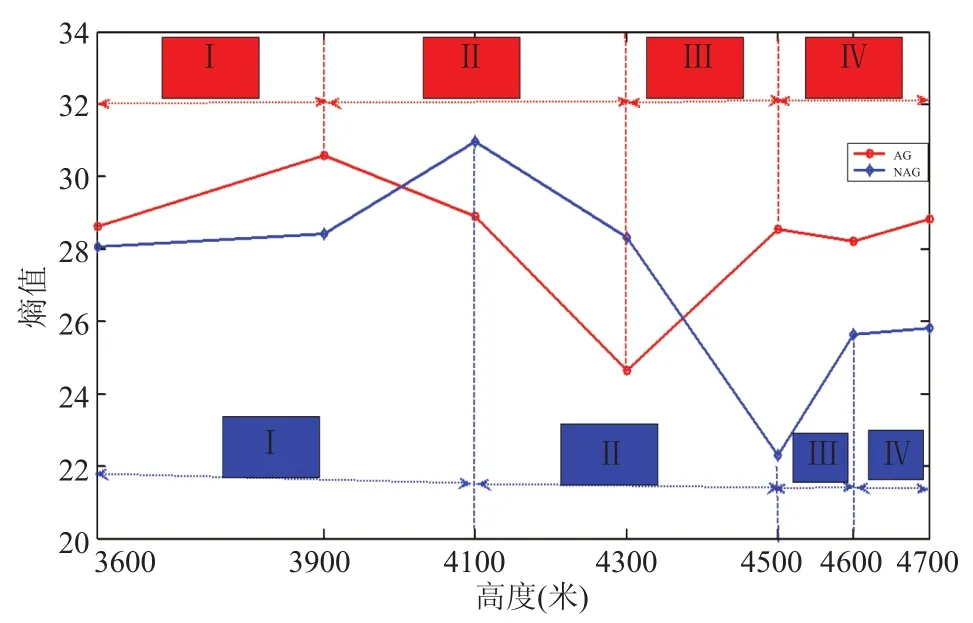
图 5 基于多尺度熵的低氧调节过程Fig. 5 The adjustment process of hypoxia based on multiscale entropy
大量事实与研究表明,预适应是机体在低于生理阂值的各种应激刺激下,不断提高其自稳态或抗损伤能力以求生存的过程[21]。机体在应激刺激后的生理反应规律可归纳为:应激打破生物体内环境的自稳态,引起机体警觉性的预适应反应,使机体抗应激能力提高,随后达到新的动态平衡(即新的自稳态),以实现进化或者在机体抗应激能力不能对付应激时,启动细胞凋亡完成优胜劣汰,即:应激→自稳态→预适应→新的自稳态或细胞凋亡的过程。
低氧预适应是指 1 次或多次短暂、非致死性低氧刺激后,机体获得的对更严重甚至致死性缺氧的耐受性。预适应是机体抗缺氧的一种内源性保护现象,预适应可以提高机体对进一步低氧的耐受能力,也称为低氧耐受性。适度的低氧应激刺激对机体产生低氧预适应效应,提高了机体适应此类应激的能力,可达到一个新的自稳态;而过强或延长的应激则可损伤组织细胞,诱导死亡。上述过程可以归纳为:低氧应激→自稳态→低氧预适应→新的自稳态或细胞凋亡。
结合实验结果和上述分析,我们把人体在低氧环境中的调节适应分为四个阶段。
(1)低氧应激阶段:在低氧刺激作用下,机体打破体内原有的自稳态。
(2)低氧适应性调节阶段:在低氧刺激作用下,机体调动自身机能,引起机体警觉性的预适应反应为向更高海拔适应做准备。此时预习服组比未预习服组,表现出调节机制启动快,适应能力强的特性。
(3)低氧预测阶段:此时预习服组比未预习服组,表现出更敏锐的低氧判断力。
(4)新的自稳态阶段:两组受试者进过自身的低氧适应与调节后,以各自的习服速率向各自的目的点迁移已达到各自新的自稳态。此时,预习服组比未预习组,具有更强的自稳态平台,更适应高海拔环境。两组受试者低氧调节过程的差异都是人的低氧记忆性的体现。
由图 5 可知,八名受试者经过适度的低氧刺激,机体产生低氧预适应效果,提高了机体适应低氧应激的能力,达到了一个新的自稳态。AG组由于实验前已经在海拔 3800 m 的高原居住三个月,自身机体已产生一定的低氧记忆,因此机体的低氧调节机制启动更快,具有更敏感的预判能力,更能适应高海拔高原环境;NAG 组没有前期的低氧储备,只能通过自身机体调节去适应低氧环境,当海拔较高,环境低氧刺激量超过机体的低氧承受能力时,机体适应低氧环境的能力会下降。因此,NAG 自稳态值低于 AG 自稳态值。两组实验对象低氧调节机制的差别,正是人体自组织低氧记忆性的体现。
5 结果与讨论
目前,低氧环境下的血氧序列分析大多采用均值法或拟合法[22-24]。图 1 为均值法分析的结果,只能反映在低氧环境下,低氧训练组与对照组血氧与海拔高度的关系,并不能真实反映在低氧环境下不同机体的低氧调节过程。此外,拟合法也只是对血氧与海拔的关系进行公式表达。由于机体的差异较大,这两种方法均不具有普遍意义,也不能很好地分析机体的低氧调节机制。
相关研究表明,非线性分析方法已成为重要的生理信号分析工具。低氧环境下基于多尺度样本熵的血氧序列分析,是一个能揭示机体低氧调节机制的动态衡量指标,可从本质上揭示不同机体应对低氧环境的调节机制。通过对不同机体的低氧调节过程的分析发现,经过一定时间低氧习服的机体再次经历一定量的低氧刺激时会启动自身已形成的低氧机制,能够快速适应低氧环境,说明机体对低氧刺激有一定的记忆性。同时也表明本文介绍的方法是一种分析人的低氧调节机制的有效方法,为相关的低氧调节机制的研究提供了一种新思路。
[1] Karinen HM, Peltonen JE, Kahonen M, et al. Prediction of acute mountain sickness by monitoring arterial oxygen saturation during ascent [J]. High Altitude Medicine & Biology, 2011, 11(4): 325-332.
[2] Muza SR, Beidleman BA, Fulco CS. Altitude pre-exposure recommendations for inducing acclimatization [J]. High Altitude Medicine & Biology, 2010, 11(2): 87-91.
[3] Jones JE, Muza SR, Fulco CS, et al. Intermittent hypoxic exposure does not improve sleep at 4300 m [J]. High Altitude Medicine & Biology, 2008, 9(4): 281-287.
[4] Insalaco G, Romano S, Salvaggio A. Periodic breathing, arterial oxyhemoglobin saturation, and heart rate during sleep at high altitude [J]. High Altitude Medicine & Biology, 2012, 13(4): 258-262.
[5] Thuraisingham RA, Gottwald GA. On multi-scale entropy analysis for physiological data [J]. Physica A, 2006, 366: 323-332.
[6] Ouyang G, Li J, Liu X, et al. Dynamic characteristics of absence EEG recordings with multi-scale permutation entropy analysis [J]. Epilepsy Research, 2013, 104(3): 246-252.
[7] 李鹏, 刘澄玉, 李丽萍, 等. 多尺度多变量模糊熵分析 [J]. 物理学报, 2013, 62(12): 12051201-12051208.
[8] Faust O, Bairy MG. Nonlinear analysis of physiological signals: a review [J]. Journal of Mechanics in Medicine and Biology, 2012,12(04), doi: 10.1142/S0219519412400155.
[9] Begum S, Barua S, Filla R, et al. Classification of physiological signals for wheel loader operators using multi-scale entropy analysis and case-based reasoning [J]. Expert Systems with Applications, 2014, 41(2): 295-305.
[10] Huo C, Huang X, Zhuang J, et al. Quadrantal multiscale distribution entropy analysis of heartbeat interval series based on a modified Poincaré plot [J]. Physica A, 2013, 392(17): 3601-3609.
[11] Aktaruzzaman M, Sassi R. Parametric estimation of sample entropy in heart rate variability analysis [J]. Biomedical Signal Processing and Control, 2014, 14: 141-147.
[12] Lim J, Kwon JY, Song J, et al. Quantitative comparison of entropy analysis of fetal heart rate variability related to the different stages of labor[J]. Early Human Development, 2014, 90(2): 81-85.
[13] Takahashi ACM, Porta A, Melo RC, et al. Aging reduces complexity of heart rate variability assessed by conditional entropy and symbolic analysis [J]. Internal and Emergency Medicine, 2012, 7(3): 229-235.
[14] Ranjit AT, Georg A, Onmultiscale entropy analysis for physiological data [J]. Physica, 2006, 366: 323-332.
[15] Anne H, Benjamin B, Guillaume M. Multiscale entropy of laser Doppler flowmetry signals in healthy human subjects [J]. Medical Physics, 2010, 37(12): 6142-6146.
[16] Soltysiński T, Golnik A, Pałko T. A multiscale entropy analysis of physiological and malignant breast tissues imaged by an optical polarimeter [J]. Polish Journal of Medical Physics and Engineering, 2007, 13(2): 65-78.
[17] 刘晓婷. 基于加速度的人体步态信息多尺度熵研究 [D]. 天津: 天津大学, 2008.
[18] Manikandan MS, Dandapat S. Multiscale entropybased weighted distortion measure for ECG coding [J]. IEEE Signal Processing Letters, 2008, 15: 829-832.
[19] Costa M, Goldberger AL, Peng C. Multiscale entropy analysis of biological signals [J]. Physical Reviewe E, 2005, 71(2): 190601-190618.
[20] Costa M, Goldberger AL, Peng CK. Multiscale entropy analysis of complex physiologic time series [J]. Physical Review Letters, 2002, 89: 068102.
[21] Yu M. Human-performance engineering at high altitude [J]. Science: Advances in High-Altitude Medicine and Hypoxic Physiology in China, 2012, 338(6113), doi: 10.1126/science.338.6113.1485-c.
[22] Burtscher M,Flatz M, Faulhaber M. Prediction of susceptibility to acute mountain sicknessby SaO2values during short-term exposure to hypoxia [J]. High Altitude Medicine & Biology, 2004, 5(3): 335-340.
[23] Huang S, Wong M, Wang J. Systemic hypoxia affects cardiac autonomic activity and vascular hemodynamic control modulated by physical stimulation [J]. European Journal of Applied Physiology, 2009, 106(1): 31-40.
[24] Brito J, Siqves P, Fabiola L, et al. Chronic intermittent hypoxia at high altitude exposure for over 12 years: assessment of hematological, cardiovascular, and renal effects [J]. High Altitude Medicine & Biology, 2007, 8(3): 236-244.
Multiscale Entropy Analysis of Blood Oxygen Sequence in Hypoxic Environment
WANG Binhua1YANG Jun2CAO Zhengtao2WANG Haitao3YU Mengsun2
1(College of Control Science and Engineering,Shandong University,Jinan250061,China)
2(Air Force Institute of Aviation Medicine,Beijing100142,China)
3(Institute of Medical Equipment Research,Academy of Military Medical Sciences,Tianjin300161,China)
Multi-scale entropy was introduced to analyze the blood oxygen sequence under hypoxic environment. Compared with mean analytical method, blood oxygen sequence analysis based on multi-scale entropy can reflect the dynamic adjustment mechanism of body hypoxia better. Multi-scale entropy, which is different from sample entropy that just estimates the difference between sequence lengthmandm+1 on the smallest scale and ignores other scales, calculates sample entropy of time series on multiple scales and reflects the irregular degree of time series on scales. The result shows that blood oxygen sequence analysis based on multi-scale entropy can identify human hypoxia endurance. This method is a reliable analytical method for studying the mechanism of hypoxic regulation of human body. The result also shows that repeated hypoxic stimulation will produce acclimatization effects on the human body which shows memory of hypoxia environment.
hypoxia; multi-scale entropy; forecast; memory
R 318.04
A
2015-03-17
:2015-03-18
国家重点基础研究发展计划(973 计划)(2012CB518200)
王彬华,博士研究生,研究方向为信号处理与数据挖掘;杨军,博士,副研究员,研究方向为睡眠分析与中医研究;曹征涛,博士,助理研究员,研究方向为生理信号分析及建模;王海涛,博士,工程师,研究方向为可穿戴医疗设备研制;俞梦孙(通讯作者),工程院院士,研究方向为航空医学工程,E-mail:yumengsun@263.net。
