子波分解重构与EEMD在火山机构地震精细刻画中的应用研究

谢兴隆，刘学清，查恩来

（1.中国地质调查局水文地质环境地质调查中心，保定 071051；2.中国地质大学 地球物理与信息技术学院，北京 100083）

子波分解重构与EEMD在火山机构地震精细刻画中的应用研究

谢兴隆1，刘学清2，查恩来1

（1.中国地质调查局水文地质环境地质调查中心，保定 071051；2.中国地质大学 地球物理与信息技术学院，北京 100083）

火山岩体有利相带的分布受火山机构主体控制，也是油气高产区和有利储层发育区，因此刻画火山机构很有意义。由于火山岩的形态多样，非均质强，地震资料一般信噪比低，反射能量弱，反射波连续性差，直接使用地震资料进行火山机构刻画存在着相当大的难度。集总经验模态分解（EEMD）和子波分解重构是当前研究较热的两种技术算法，其主要特点都是突出有效信号。这里尝试使用这两种方法分别对火山机构的地震数据进行分解研究，两种方法虽然本质不一，但效果类似，为火山机构的刻画提供了较为可靠的依据。

火山机构刻画；集中经验模态分解；子波分解重构

0 引言

火山岩作为岩性油气藏中重要的一员，正越来越受到国际石油界的广泛重视，火山岩油气藏已经成为勘探开发的新领域［1］。火山岩气藏主要由气源岩、火山圈闭以及断裂疏导通道控制［2］，其产能与火山机构有着直接关系。火山机构的识别在火山油气藏勘探和开发具有十分重要的作用，火山机构的主体分布，一直都是国、内外油气勘探的重点。火山机构主体控制着火山岩体相带的分布，而且也是油气高产区、火山岩有利储层的发育区。但是由于火山岩的形态多样，非均质强，地震资料一般信噪比低，反射能量弱，反射波连续性差，直接使用地震资料进行火山机构刻画存在着相当大的难度。

集总经验模态分解（EEMD）和子波分解重构是当前研究较热的两种技术算法，两种算法原理不同，侧重点不一，但其方法的主要特点都是可以在信息丰富的地震数据中分解突出有效信号。近年来，针对经验模态分解的研究主要在时频分析、地震信号去噪、地震相、地震属性等方面［3－5］；子波分解重构技术主要被应用在油气性检测、识别薄互层、储层预测等方面［6－10］。作者尝试使用两种方法进行分解，得到了刻画火山结构边界的地震依据，取得了一定效果。

1 方法原理

1.1 集总经验模态分解（EEMD）

集总经验模态分解（ensemble empirical mode decomposition，简称EEMD）［11］是针对经验模态分解（empirical mode decomposition，简称EMD）［12－13］中的模态混叠现象，由Wu等［11］提出的改进算法。经验模态分解适合于分析非线性、非平稳信号序列，具有很高的信噪比。该方法是对信号的一种自适应分解，可以分解出代表某种特定意义的固有模态函数（intrinsic mode function，简称IMF）。

EEMD是一种噪声辅助数据处理技术，主要是依据正态分布白噪声在EMD中具有二阶时间尺度分解特性及不同白噪声序列对应IMF之间的无关性［14］，一方面提供了均匀分布的分解尺度，有效避免模态混叠，另一方面平滑了其他干扰，很大程度上抑制了干扰信号。EEMD的算法流程如下：

1）将一定比例白噪声附加在原始信号中。

2）将附加了白噪声的信号进行EMD分解，得到若干固有模态函数IMF。

3）分别对信号附加不同的白噪声，循环进行以上两步操作。

4）将多次分解得出的相应IMF取平均作为最后的结果。

最后得到集总平均结果用公式表示为式（1）。

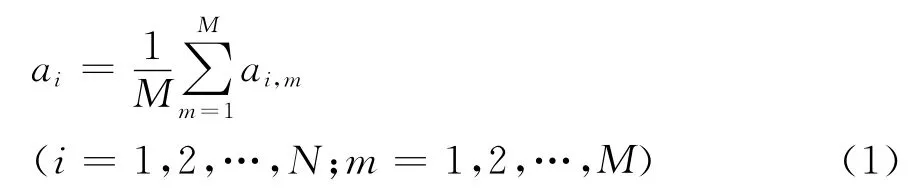
其中：ai，m为第m次加白噪声分解的第i个IMF分量；N为IMF分量个数；M为集总模式总次数。

需要指出的是，由于每次EMD分解添加不同白噪声，噪声之间不相关，因此对所有EMD分解后的IMF取平均后，人为添加的白噪声被抵消，多次分解就是为了消除附加的噪声。

1.2 多子波分解重构

Lilly等［15］提出了多子波变化的新技术，目前运用的多子波分解技术基本上是基于这个原理上的改进。通常在地震资料处理解释中，使用的是传统地震道模型，即地震道被定义为地震子波与地层反射系数的褶积［16］，数学公式表达为式（2）。

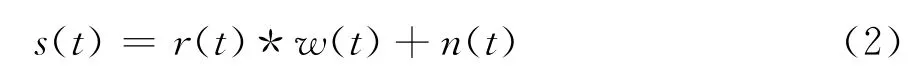
式中：r（t）为地层的反射系数序列；w（t）为地震子波；n（t）为噪声项。

由于地震子波在实际情况下随时空而变化，采用传统地震道模型处理或解释，就可能丢失一些反映地层或岩性特征及变化的有效信息，甚至会造成一些假象。如果要提高地震处理解释的准确度，需要从根本上改进地震道模型，多子波地震道模型应运而生。多子波地震道模型的数学表达式为式（3）。

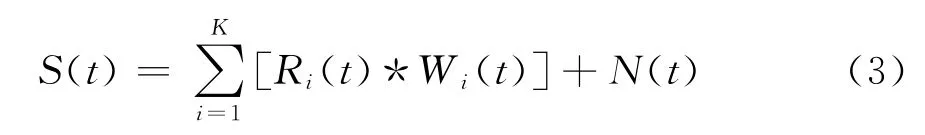
其中：Ri（t）为第i个地层对应的反射系数；Wi（t）为对应的地震子波；N（t）为噪声项。

多子波分解可以将地震数据分解成一系列不同振幅、频率的子波，子波的类型可以是Gabor，Morlet，Rick等子波，然后根据已知研究目标的子波特征进行重构得到新的重构数据体，从而找出规律性的变化。实现多子波重构分解的数学方法也很多，如小波变换、S变换、希尔伯特－黄变换、匹配追踪等算法［17］。由于分解是线性的，将分解后的子波重新叠加，就可以得到被分解的地震道。

地震子波分解重构本质上与滤波不同，滤波一方面消弱了干扰波的能量，但同时也使有效波受到一定的损害，主要体现在能量与频率上；而子波分解重构先将噪声剔除，再将剩下的部分重构，不仅去除了噪声，而且没有造成有效信号的伤害。

2 应用实例分析

不同的喷发方式和地下物源特征决定了火山的形态和岩性特征，在地震剖面上产生不同的反射特点，以反射特征划分，一般可以分为杂乱状反射火山机构和层状反射火山机构两大类，①杂乱状反射火山机构喷发强度大，形成的火山锥体非常明显，地震反射外形呈楔状，倾角大；②层状反射火山机构火山喷发强度相对较小，火山碎屑物从空中坠落堆集成火山碎屑岩，或者热碎屑流堆积而成，多期喷发叠置构成了层状反射火山机构，火山机构边界不清晰。这里主要是以这两种类型的火山机构为例进行说明，选用的地震资料来自松辽盆地北部某处油田。

2.1 地震数据分解效果分析

2.1.1 EEMD分解效果分析

本次所使用的EEMD分解添加的白噪声比例为10%，计算次数选择为120次。使用EEMD对原始地震数据进行分解，共得到了11个IMF分量。如图1所示为850线277道的地震数据分解图，在图1中纵坐标均为振幅，横坐标为时间。从图1中可以看出IMF1分量道IMF11分量频率依次下降，从第6个IMF分量开始，从分量可以看到的有效信息越来越少，分量形态、振幅均和原始数据有着巨大差异。必须要说明的是，IMF1分量主要是由附加噪声残余量以及原始数据中噪声组成。

如表1所示，IMF各分量的相关系数和方差贡献率差别较大，从IMF6开始，相似系数均在在0.1以下，方差贡献率均在0.5%以下，可以说从分量IMF6开始的其他分量所含有的有效信息较少，研究意义不大。

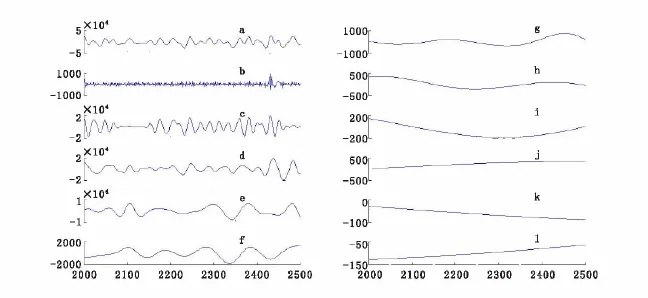
图1 由EEMD分解的各个地震道分量Fig.1 The seismic components decomposed by EEMD

表1 IMF地震分量相关系数及方差贡献率Tab.1 The correlation coefficients and contribution rates of IMF components

2.1.2 子波分解重构效果分析

本次子波分解重构的子波范围设定在1Hz～80Hz，选用的子波类型为Rick子波。为了验证子波分解重构的合理性，特重构出了全子波地震数据，即重构数据子波范围为1Hz～80Hz。图2展现的是686线277道原始数据与全子波数据对比图，由图2可以看出两者形态基本一致。使用子波重构数据减去原始地震数据即得到子波重构数据的误差，误差曲线如图3所示，总体来说误差曲线的形态和原始地震数据形态一致。经过计算子波重构数据的相对误差不足3.8%，计算公式为式（4）。

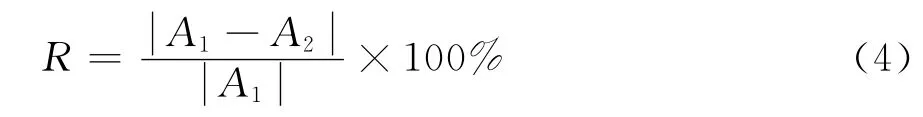
式中：R为相对误差系数；A1为原始信号振幅；A2为全子波重构后的信号振幅。说明此处地震数据使用子波分解重构是合理的。

由于本区所要研究的对象是火山机构，反射规律复杂，信号变化快，故不能以沉积岩重构标准进行，频率范围很小的重构对整个火山机构的刻画是不利的。因此为了刻画的整体效果，本次子波重构数据的子波频率范围选的较大。

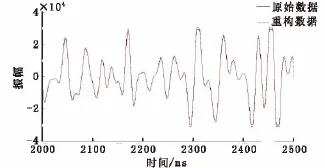
图2 原始数据与全子波重构数据波形图Fig.2 The waveform of original data and full－wavelets reconstruction data

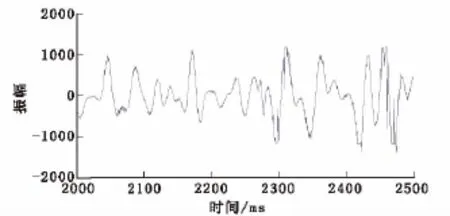
图3 全子波误差曲线Fig.3 The error curve of full－wavelets reconstruction

2.2 杂乱反射火山机构

以A井附近的火山机构为例，首先分析低频分量剖面（图4）。在原始剖面中，火山机构的上凸特征非常明显，但火山机构的外部轮廓能量不一，时断时续，尤其是内部反射杂乱，难以看出具体规律；IMF4分量剖面的频率较低，但反应大的地质背景效果较好，结合钻井地质分层，可以看出外部丘状反射轮廓，另外内部反射也表现出了一定的规律性，大致描述了火山岩层的展布状态，反映出了火山岩石流的流动方向和下超趋势；子波重构的低频剖面反映内容类似，但效果稍差些。

图4 过A井火山机构原始地震剖面与低频分量对比图Fig.4 The comparison of original data and low frequency component in through－A well seismic section

高频分量有着较高的分辨率，但是和原始剖面相比，缺少宏观的地层背景。高频分量主要反映了一些细节，为了便于说明在剖面中画了A与B两个区（图5）。F1断裂是本区一条重要的断层，如红色圈内所示，在原始地震剖面中断裂两端的同相轴强度相似，有一定的连续性，而在IMF2分量剖面和子波重构的高频剖面中F1断裂上盘的原强同相轴变为了两个弱同相轴，明显反应出貌似连续的同相轴不是同一地层，这和层位解释结果一致。对比B框中的剖面细节图可以看出，IMF2分量与子波重构的高频分量分辨率较高高，IMF2分量效果更好些，原来较为杂乱的地方也表现出较好的成层性。

在解释中我们将火山机构的下超终止作为火山机构的边界，但是火山机构究竟在何处下超终止，在原始剖面中只能根据大体趋势加上解释员的经验来划分，缺少剖面特征的依据。图6为A框内的地震剖面细节图，图6中蓝线为一地层顶面的解释层位，也相当于火山岩旋回的底面，可以肯定的是火山机构便是下超终止于该层面的。IMF2剖面与子波重构剖面都反映出了火山岩层的下超趋势，如图6中红色虚线所示，明确指示了火山岩层的下超方向，根据这个方向可以将火山机构的终止位置确定在第400道附近。

2.3 层状反射火山机构

本次以B井附近火山机构为例，由钻井资料可知，B井处发育有两期火山机构，C井处发育有一期火山机构。由于火山机构规模并不是很大，频率较低展现大背景的IMF4分量与低频子波重构分量在此处作用不大。

作者重点分析高频分量，由图7可知，高频分量的分辨率明显高于原始数据，两种方法的高频剖面显示效果类似，这也相互说明提供的刻画依据是合理的。从合成记录可以看到第一期次火山岩底面有一波峰，如图7中蓝色箭头指向所示，而原始地震记录上却很难找到与此对应的同相轴，在IMF2剖面与子波重构的高频分量中都可以清楚地看到与此合成记录波峰对应的同相轴，这为解释火山机构底界面提供了直接证据。而且该层发育的火山机构边界在高频分量中也存在着明显的下超终止、同相轴变弱等特点。最后根据高频分量剖面的分析结果，结合原始地震记录，在钻井地质分层及解释层位的约束下对B井附近的火山机构进行精细刻画，两期次火山机构的大致形态如图7（b）中虚线包围部分所示。

3 结论

根据研究内容，结论主要有以下几点：

1）EEMD是自适应分解，分解完成后高频和低频分量就已经确定；子波分解重构可以按照频率范围重构出多个高频、低频分量。

图5 过A井火山机构原始地震剖面与高频分量对比图Fig.5 The comparison of original data and high frequency component in through－A well seismic section

图6 方框A内地震剖面细节对比图Fig.6 The detail comparison of seismic section in box A

2）两种方法得到的低频分量表现出了火山机构的宏观趋势，主要体现在杂乱反射火山机构；两种方法得到的高频分量都突出了火山机构在原始剖面没有的细节，为火山机构的刻画提供了地震依据，尤其在层状反射火山机构的刻画上表现较好。

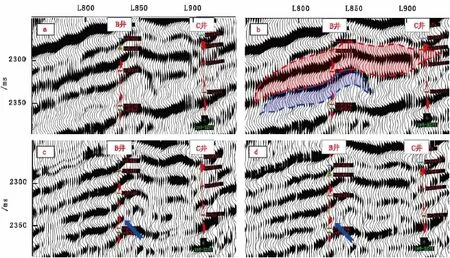
图7 过B井火山机构原始剖面与高频分量剖面对比图Fig.7 The comparison of original data and high frequency component in through－B well seismic section

3）EEMD与子波分解重构有着本质的区别，地震剖面也不尽相同，但表现效果类似，这两种方法的相互验证从侧面也说明为火山机构刻画提供的地震依据可信度较高。

［1］ 姜洪福，师永民，张玉广，等.全球火山岩油气资源前景分析［J］.资源与产业，2009（03）：20－22.

JIANG H F，SHI Y M，ZHANG Y G，et al.Potential of global volcanics－hosted oil－gas resoruces［J］.Resources and Industries，2009（03）：20－22.（In Chinese）

［2］ 唐华风，王璞珺，李瑞磊，等.松辽盆地断陷层火山机构类型及其气藏特征［J］.吉林大学学报：地球科学版，2012（03）：583－589.

TANG H F，WANG P J，LI R L，et al.Classification of volcanic edifices and its characteristics of gas pool in faulted sequence of the songliao basin，NE china［J］.Journal of Jilin University：Earth Science Edition，2012（03）：583－589.（In Chinese）

［3］ 刘庆敏，杨午阳，田连玉，等.基于经验模态分解的地震相分析技术［J］.石油地球物理勘探，2010（S1）：145 －149.

LIU Q M，YANG W Y，TIAN L Y，et al.Seismic facies analysis technique based on the empirical mode decompositon［J］.Oil Geophysical Prospecting，2010 （S1）：145－149.（In Chinese）

［4］ HUANG Y P，GENG J H，ZHONG G F，et al.Seismic attribute extraction based on HHT and its application in a marine cabonate area［J］.Applied Geophysics，2011（02）：125－133.

［5］ 陈伟，王尚旭，啜晓宇.基于经验模态分解的属性优化方法［J］.石油地球物理勘探，2013（01）：121－127.

CHEN W，WANG SH X，CHUAI X Y.Seismic attributes optimization based on the empiri－cal mode decompostion［J］.Oil Geophysical Prospecting，2013 （01）：121－127.（In Chinese）

［6］ AN P.Application of multi－wavelets seismic trace decomposition and reconstruction to seismic data interpretation and reservoir characterization［J］.SEG

Technical Program Expanded Abstract，2006（25）：973－976.

［7］ AN PING.Case studies on stratigraphic interpretation and sand mapping using volume－based seismic waveform decomposition［J］.SEG Technical Program Expanded Abstract，2006（25）：496－498.

［8］ 黄跃，许多，文雪康.多子波分解与重构中子波的优选［J］.石油物探，2013（01）：17－22.

HUANG Y，XU D，WEN X K.Optimization of wavelets in multi－wavelet decomposition and recon－struction method［J］.Geophysical Prospecting for Petroleum，2013（01）：17－22.（In Chinese）

［9］ 佘刚，周小鹰，王箭波.多子波分解与重构法砂岩储层预测［J］.西南石油大学学报：自然科学版，2013（01）：19－27.

SHE G，ZHOU X Y，WANG J B，Prediction of sand reservoir with multi－wavelet seismic trace decomposition and reconstruction［J］.Journal of Southwest Petroleum University：Science and Technology Edition，2013（01）：19－27.（In Chinese）

［10］代双和，陈志刚，于京波，等.多子波分解与重构技术在阿尔及利亚TKT—NGS油田储层描述中的应用［J］.石油地球物理勘探，2011（01）：103－109.

DAI SH H，CHEN ZH G，YU J B，et al.Application of multi－wavelet decomposition and reconstruction technique in reservoir characterization in TKT－NGS oilfield，Algeria［J］.Oil Geophysical Prospecting，2011（01）：103－109.（In Chinese）

［11］WU Z，HUANG N E.Ensemble empirical mode decomposition：a noise－assisted data analysis method ［J］.Advances in Adaptive Data Analysis，2009，1 （1）：1－41.

［12］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－station time series analysis［J］.Proceeding of the Royal Society of London A，1998，454：903－995.

［13］HUANG N E，SHEN Z，LONG S R.A new view of nonlinear water waves：the Hilbert spectrum［J］.Annual Review of Fluid Mechanics.1999，31：417－457.

［14］WU Z，HUANG N E.A study of the characteristics of white noise using the empirical mode decomposition method［J］.Proceedings Of The Royal Society.A 2004，460：1597－1611.

［15］JONATHAN M，LILLY JEFFREY PARK.Multiwavelet spectral and polarization analyses of seismic records［J］.Geophysical Journal International，1995，122（3）：1001－1021.

［16］陆基孟.地震勘探原理［M］.北京：石油工业出版社，1993.

LU J M，The principle of seismic exploration［M］.Beijing：Petroleum industry press，1993.（In Chinese）

［17］徐天吉，沈忠民，文雪康.多子波分解与重构技术应用研究［J］.成都理工大学学报：自然科学版，2010，37 （6）：660－665.

XU T J，SHEN ZH M，WEN X K.Research and application of multi－wavelet decomposition and reconstructing technology［J］.Journal of Chengdu University of Technology：Science and Technology Edition，2010，37（6）：660－665.（In Chinese）

Application research of wavelet decomposition and reconstruction and EEMD on volcanic edifice seismic depiction

XIE Xing－long1，LIU Xue－qing2，ZHA En－lai1
（1.Center for Hydrogeology and Environmental Geology Survey，CGS，Baoding 071051，China；2.China University of Geosciences，Geophysics and Information Technology Institute，Beijing 10083，China）

Depiction of volcanic edifice is very important because it controls the distribution of volcanic lithofacies and is usually fine reservoir development region.However，it is very hard to depict volcanic edifice directly using seismic data due to obvious heterogeneity of volcanic rock and low SNR of seismic data.Ensemble empirical mode decomposition（EEMD）and seismic wavelet decomposition and reconstruction are hotspots in current study，these two methods can have good results in getting effective signal.This paper attempts to decompose seismic data of volcanic edifice by these two methods.These two methods have similar effects despite of different starting point，which provides basis for volcanic edifice depiction.

depiction of volcanic edifice；ensemble empirical mode decomposition；wavelet decomposition and reconstruction

P 631.4

：A

10.3969／j.issn.1001－1749.2015.06.14

1001－1749（2015）06－0754－07

2014－12－08改回日期：2015－04－11

重要矿产资源调查计划（12120115037401）

谢兴隆（1989－），男，硕士，主要从事地球物理勘探与方法研究工作，E－mail：xxl0306＠126.com。