基于Doppler辅助的飞行器惯导系统空中对准研究

于德新，潘爽，岳昆

(1.海军潜艇学院训练部，山东 青岛 266043；2.海军潜艇学院战略导弹与水下兵器系，山东 青岛 266043)

基于Doppler辅助的飞行器惯导系统空中对准研究

于德新1，潘爽2，岳昆2

(1.海军潜艇学院训练部，山东 青岛 266043；2.海军潜艇学院战略导弹与水下兵器系，山东 青岛 266043)

针对Doppler/SINS组合导航系统在飞行状态下的导航精度较差的问题，提出了利用载体作匀速圆周运动的初始对准方法. 该方法可以快速估计出SINS的平台失准角并能提高对平台失准角的估计精度，可以较大幅度地缩小对平台失准角估计的稳态极限值。模拟试验验证了该方法的可行性和有效性，具有较好的工程应用前景。

Doppler/SINS；空中对准；EKF；匀速圆周运动

0 引言

由于惯导装备现状及理论研究水平的影响，现有的飞行器惯导设备还不足以依靠自身解算完成空中对准的任务。多数学者倾向于立足现有装备，通过借助其他任务设备(如Doppler测速仪、高度表、测速雷达、航姿系统等)的辅助改善惯导的解算性能，或是以GPS、Glonass等成熟卫星定位系统，或者是我国北斗系统的辅助信息为基准完成姿态失准角的估计与补偿，这种基于自身设备(包括机载导航设备、任务设备等)辅助的SINS空中对准方式也称为空中组合对准，或称为单机辅助对准。

Doppler测速雷达有测速精度高的优点，所以可以用它测出的速度信息进行辅助动基座对准。多普勒装置一般被认为是与飞行器固连的(也有一些通过机械平台稳定并与载体的运动隔离的多普勒装置)。多普勒速度误差包括装置固有的误差，例如刻度误差、偏置和噪声，还有来自装置的安装误差如结构未对准(视轴)。偏置和比例因子/视轴误差可认为是随机常数。对于基于雷达原理的多普勒装置，噪声可能是载体速度的函数并且通常被看作是“起伏”噪声。

1 Doppler及组合系统误差模型

多普勒测速雷达的测速原理是利用电磁波在空间传播时遇到运动目标时产生多普勒效应来进行的。即当雷达发送的电磁波(频率为f0)遇到运动目标时所产生的回波信号频率为f0± fd，fd为多普勒频移，它与目标到雷达的径向距离Vr的关系为：fd= 2f0×Vr/(c + Vr)。其中，c为光速，一般情况下c＞＞Vr。由此得Vr= fd×(λ0/2)，其中，λ0= c/f0为发射电磁波的波长。所以只要测得fd(f0和c已知)即可求出径向速度Vr。

多普勒雷达的测速误差主要由以下几方面组成：① 发射机频率变化造成的误差(0.0048%)；② 光速在空气中的变化造成的误差(0.023%)；③ 测量方法造成的误差(0.0002%)；④ 时钟频率的不稳定性造成的误差(0.005%)；⑤ 信号经过接收机、输入放大器和带通滤波器时相位发生变化引起的误差(0.02%)；⑥ 在数据处理装置中设有磁带记录仪，当信号经过记录仪进行重放测量时，由于磁带记录仪的时间基准误差引起的测量误差(0.1%)。综合上述各种误差，测速雷达的测速误差约为0.1031%，满足导航的精度要求[1]。

多普勒速度传感器的一个通用误差模型为：

在这个模型中，离轴、速度相关的项代表未对准误差或者视轴误差。dBSyz和dBSzx项分别代表方位和俯仰视轴误差。对于固定翼飞行器的应用，多普勒装置的误差与飞行器速度分量和的乘积，相对多普勒装置的偏置项来说，通常是非常小以至于可以忽略不计。

将多普勒速度传感器的输出与惯性导航系统的速度结合起来，组成一个测量值用于机上Kalman滤波算法的处理。多普勒速度与惯性导航系统的速度之差称为多普勒偏差，可表示为[1,38]：

图1 SINS雷达对准程序Fig.1 Alignment procedure of SINS with aid of radar

2 数学模型与对准方案设计

首先，惯导系统利用地球自转角速率和重力加速度进行自主式粗对准，然后把测速雷达测量的速度与惯导的速度匹配，利用Kalman滤波器对状态进行估计，并根据状态估计值对惯导系统进行修正，完成惯导系统的初始对准，其原理图设计如图1所示。

通过Kalman滤波器进行信息融合，并利用其输出的参数误差估计值直接校正系统输出的导航参数，在校正方式上采取输出校正与反馈校正相结合的方法。估计过程中首先采用输出校正，等滤波器稳定(即估计误差稳定)后进行反馈校正，并以校正后的导航参数作为导航参数输出。导航解算流程如图2所示。

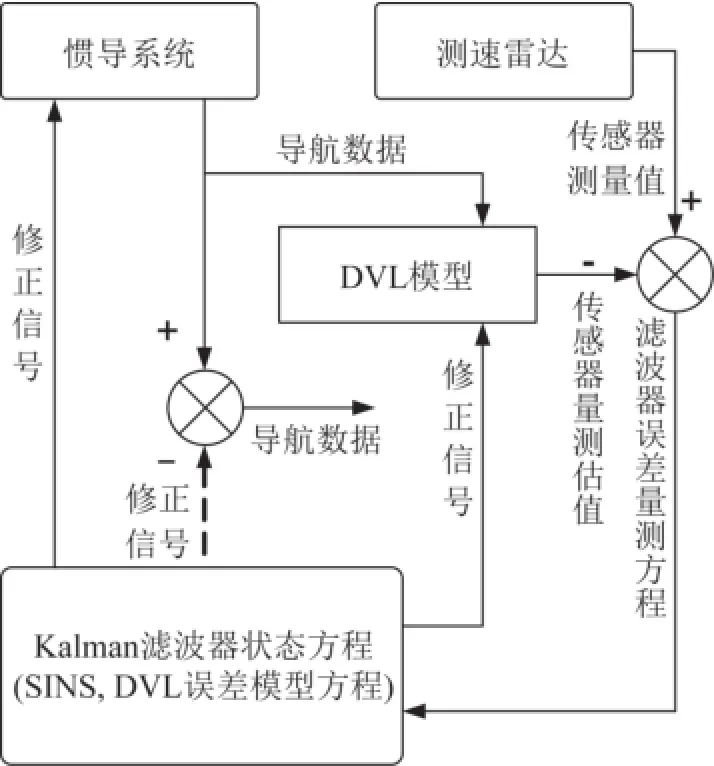
图2 SINS雷达导航程序结算流程Fig. 2 Navigation procedure of SINS with aid of radar

2.1 Doppler/SINS空中对准数学模型

A. 系统状态方程

对准过程中，飞行器在水平面作缓慢的回转运动，高度通道与水平通道的耦合影响较弱，且高度通道采用气压高度表等辅助测高设备进行阻尼，所以在近似水平回转中，高度通道参数变化微小，可以忽略高度通道的影响。导航系采用东北天地理坐标系，选取系统初始对准的状态向量为：

其中，φE，φN和φU为姿态失准角；δVx和δVy为东向、北向速度误差；δλ和δL为经度、纬度误差；εx，εy和εz为侧向、纵向和垂向陀螺的漂移；δVd为速度偏移误差；ε⊿为偏流角误差；δC为刻度系数误差。

系统状态方程如下：

其中，fE，fN和fU分别为加速度计所测比力在导航系上的分量；VE，VN，L和λ为导航系统参数输出；和为加速度计的随机噪声，服从零均值正态分布。

B. 系统量测方程

取SINS解算速度和Doppler雷达测量速度之差作为观测量，系统观测向量为：

2.2 滤波器设计

上述的状态方程和观测方程可以表示成：

式中，kd表示考虑偏流角的航迹方向。

系统的状态方程为连续线性，观测方程是离散线性的。将状态方程离散化为

离散Kalman滤波方程如下：

3 仿真与结果分析

3.1 仿真环境设置

在仿真试验中，由于对准时飞行器主要做短时间的圆周运动，因此可以简化之前建立的惯导误差模型，初始仿真参数设定为：

(1)初始位置为30°N，120°E；初始方位、俯仰和横滚角分别为0°、0°和0°；初始水平姿态失准角为6角分、方位姿态失准角为10角分；

(2)飞行轨迹设计：飞行器以60m/s的速度在前50s做爬升运动，其后50s以60m/s速度作匀速直线飞行，此后300s做盘旋机动，盘旋角速度10°/s，盘旋中飞行器滚转角为30°，盘旋结束后作匀速平飞，仿真总时间为400s；

(3)SINS采用中等精度(1n mile/s)系统，陀螺漂移相关时间为=10800s，陀螺常值漂移和随机漂移分别为0.02(°)/h和0.01(°)/h(1σ)，随机常数均方根为4.8×10-8rad；加速度计零偏相关时间为10800s，常值偏置和随机偏置分别为10-4g和 5×10-5g(1σ)，常数均方根为4.8×10-8rad。

3.2 实验结果及分析

飞行器作机动飞行，轨迹包括爬升、变速、平飞、盘旋等各种飞行状态。仿真总时间为400s，对准在圆周盘旋中完成，其间Doppler/ SINS的解算数据与GPS测量的位置、速度信息进行融合，完成对准过程。图3-图5给出了初始对准时位置误差、速度误差及失准角估计误差。

图3 对准定位误差Fig. 3 Localization error in alignment

图4 飞机对准速度误差Fig. 4 Velocity error of airplane in alignment

图5 捷联惯导系统的对准误差Fig. 5 Misalignment error of SINS in alignment

仿真图3～5表明，基于Doppler雷达的SINS动基座对准方案，在经过不大于30秒的滤波解算后，滤波误差趋于稳定，姿态失准角估计误差分别为：ΔφE= 25.7″、ΔφN= 26.4″、ΔφU= 3.24′；速度误差分别为：ΔVE= 0.46m/s、ΔVN= 0.39m/s。此外，飞行中由GPS辅助SINS的位置匹配定位误差为：ΔL = 12.7m、Δλ= 15.3m。

仿真结果验证了Doppler/SINS组合对准方案的可行性，并在很短的时间内得到了比较精确的对准结果。此外，仿真表明EKF滤波算法有效解决了观测噪声的不确定性问题，提高了收敛速度。与相关文献所说的3个失准角的稳态误差是对准的“极限精度”且“无法消除”的理论相比，该方法的确是抑制陀螺和加速度计随机误差的一种有效方法。另外，为了得到精确的三维速度信息，·综合多种因素得到最优的雷达输出就显得很重要。

4 结论

本文针对SINS/GPS组合导航系统地面静基座对准影响飞行器响应时间的问题，提出了一种基于Doppler观测量和圆周运动对准过程的SINS/Doppler空中应急对准方法。

通过理论分析，建立了系统的状态方程和量测方程 ,跑车试验验证了该方法的可行性和有效性。该方法可较大程度地提高系统的初始对准速度和精度。与相关文献中所说的3个失准角的稳态误差是对准的“极限精度”且“无法消除”的理论相比，该方法的确是抑制陀螺和加速度计随机误差的一种好方法。可以指出，将一个高精度的单轴速率转台与SINS组合成一个系统是一种工程实现的有效途径。

[1] NOAA. Measured Values of Global Positioning System(GPS) time[S]. www.noss.gov. 2008.06.

[2] Jamshaid Ali, Muhammad Ushaq. A consistent and robust Kalman filter design for in-motion alignment of inertial navigation system[J]. Measurement, 2008, 10(2): 1-6.

[3] Wang Xinlong, Guo Longhua. An intelligentized and fast calibration method of SINS on moving base for planed missiles[J]. Aerospace Science and Technology, 2009, 4(4): 1-8.

[4] Wang Xinlong. Fast alignment and calibration algorithms for inertial navigation system[J]. Aerospace Science and Technology, 2009, 04(02): 1-6.

[5] Joon Goo Park, Jinwon Kim,and Jang Gyu Lee. The Enhancement of INS Alignment Using GPS Measurements, IEEE Position,Location and Navigation Symposium, 1998.01: 534-540.

[6] Dr.Min-James Chang. Rapid-fight/Transfer Alignment Filter for GPS/INS/DVS Navigation System, Proceedings of the ION, National technical meeting, Santn Monica, CA, 1997, 01: 14-16.

[7] Chan Gook Park, Kwangjin Kim. UKF based In-flight Alignment using Low Cost IMU[J]. AIAA GNCCE. 2006,08: 1-12.

A study of the Flight Alignment of Aircraft Inertial Navigation System with the Aid of Doppler

YU Dexin1, PAN Shuang2, YUE Kun2
(1. The training department, Navy submarine academy, Qingdao 266043, China; 2. Strategic missile and underwater weapon system, Navy submarine academy, Qingdao 266043, China)

An in-flight alignment algorithm was proposed by utilizing a uniform circular motion of the aircraft to improve the accuracy of Doppler/SINS integrated navigation system in flight condition. With the proposed theory, the platform error-angles of the SINS can be estimated quickly, the estimation accuracy can be improved and the steady-state limit of platform error-angles can be greatly narrowed down. Simulation experiment verifies the feasibility and effectiveness of this theory which has a prospect engineering application value.

Doppler/SINS; in-flight alignment; EKF; uniform circular motion

10.3969/j.issn.2095-6649.2015.02.07

本论文受国家自然基金项目(基金号：61473306)资助

于德新(1980-), 男, 硕士, 讲师, 研究方向: 兵种战术的研究; 潘爽(1981-), 女, 博士生, 研究方向: 导航系统初始对准、鲁棒滤波理论的研究。

于德新，潘爽，岳昆．基于Doppler辅助的飞行器惯导系统空中对准研究[J]．新型工业化，2015，5(2)：38-43