中国服务业增长、要素投入与技术效率的动态关系分析——基于脉冲响应函数的实证研究

王铁山

（1.西安工程大学管理学院，陕西西安710048；2.西安工业大学经济管理学院，陕西西安710032）

中国服务业增长、要素投入与技术效率的动态关系分析
——基于脉冲响应函数的实证研究

王铁山1、2

（1.西安工程大学管理学院，陕西西安710048；2.西安工业大学经济管理学院，陕西西安710032）

本文基于向量自回归（VAR）模型，运用脉冲响应函数、方差分解等方法，对改革开放以来（1978—2012年）中国服务业增长、劳动力和资本投入、技术效率之间的关系进行了研究，结果表明这四者之间存在着长期稳定的动态关系，彼此之间互相作用、互相影响。其中，服务业增长对技术效率有正向影响作用，服务业劳动力和资本投入对技术效率有负向影响作用，这种动态效应的积累是形成当前中国服务业技术效率现状及地区差异的内在原因。

服务业；技术效率；脉冲响应函数

一、引言

改革开放以来，随着中国对服务业的重视程度不断提高，对服务业的劳动力和资本要素投入不断增加，服务业得到了持续发展。随之而来的是服务业的技术效率不断变化，这与服务业的增长以及劳动力和资本要素的投入变化密不可分。技术效率是用来衡量经济系统的产出、劳动力和资本等要素投入变量之间的投入产出比例关系即水平高低的指标，这些因素之间的相互作用及变化会导致技术效率的变化。然而，目前还没有学者对这四者之间的相互影响关系进行研究，只有部分学者探讨了不同影响因素对服务业技术效率的影响效应。

顾乃华和李江帆[1]认为，影响服务业技术效率的因素主要有市场化程度、劳动力素质、起点因素、资本密集度。之后，顾乃华[2]进一步认为，服务业技术效率主要受起点因素、就业人员教育水平的变化、市场化推进程度以及资本密集度变化的影响。任英华和王耀中[3]认为，工资、劳动者素质、信息技术等对服务业技术效率有影响。杨青青等人[4]认为，人力资本、信息化水平、市场化水平、社会资本对服务业技术效率有重要作用。徐盈之和赵玥[5]发现，信息化水平、研发投入和城市化水平是影响信息服务业区域差异的因素。谷彬[6]发现，市场化程度、对外贸易、外商直接投资、政府行为、工业化水平是影响服务业技术效率的重要因素。黄莉芳、黄良文和洪琳琳[7]认为，专业化水平、规模经济和市场化水平是影响生产性服务业技术效率的重要因素。许建平和任燕[8]发现，各区域在经济发展程度、经济开放程度、城市化水平、工业化程度、收入与消费水平、科技水平、人力资本要素水平、基础设施水平等方面的差异是服务业区域发展差异形成的重要影响因素。刘中艳[9]发现，人力资本、产业融合、产业集聚度、市场化水平对现代服务业的发展皆具有不同程度的影响作用。邵金菊和王培[10]发现，科技创新能力、基础设施水平和城市化水平对软件服务业投入产出效率有显著影响。殷凤和张云翼[11]发现，市场化程度、劳动投入质量、城镇化、对外贸易、外商直接投资对服务业技术效率有影响。

可见，当前有关研究都没有关注服务业技术效率与服务业增长、要素投入之间互动作用的动态关系，研究这四者之间的关系具有一定的理论和现实意义。因此，本文分析这四者之间的联动关系，在此基础上探讨中国服务业技术效率现状及区域差异形成的原因，并为提升中国服务业的技术效率提出相应的对策建议。

二、研究模型、变量选取与数据说明

1.研究模型

本文利用向量自回归（Vector Auto-regresion Model，VAR）模型以及在此基础上的脉冲响应函数和方差分解方法，分析改革开放30余年来中国服务业技术效率、服务业增长、劳动力投入和资本投入四者之间的相互作用及动态关系。

（1）向量自回归（VAR）模型

向量自回归模型（VAR）把系统中每一个内生变量作为系统中所有内生变量滞后项的函数来构造模型，从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型，是处理多个相关经济指标的分析方法。VAR模型的一般表达式为：

式（1）中，Yt是k维的内生变量，Yt-i（i=1，2，…，n）是滞后内生变量，Xt是d维外生变量，p、r分别是内生变量和外生变量的滞后阶数。Ai是k×k维系数矩阵，Bi是k×d系数矩阵，这些矩阵都是待估计的参数矩阵。εt是由k维随机误差项构成的扰动向量，它们相互之间可以同期相关，但不能与各自的滞后值相关，也不能与等式右边的变量相关。

（2）基于VAR模型的单位根检验与约翰森（Jo⁃hansen）协整检验

在对变量的数据进行分析前，首先对数据进行平稳性检验。本文采用单位根检验，非平稳的变量序列如果存在单位根，一般都显示出明显的记忆性和波动的持续性，可以通过差分方法消除单位根而得到平稳序列。对多个变量之间协整关系的检验采用约翰森协整检验方法，这是一种以VAR模型为基础的检验回归系数的方法。考虑如式（1）所示的VAR模型，其中，Yt是k维的非平稳的I（1）变量，Xt是d维的确定的外生变量。将式（1）改写为以下形式：

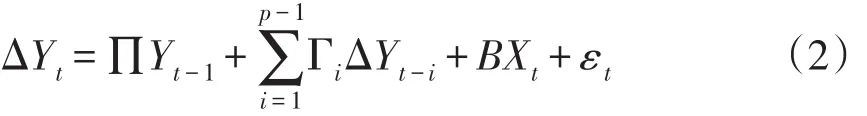
（3）基于VAR模型的脉冲响应函数

脉冲响应函数（Impulse Response Function，IRF）是衡量来自某个内生变量随机扰动项的一个标准差冲击（称之为脉冲）对VAR模型中所有内生变量当前值和未来取值的影响。脉冲响应函数的分析结果可以刻画不同影响因素引起的服务业技术效率变动的动态过程。这里以包含两个内生变量的VAR模型为例来说明脉冲响应函数的基本步骤。

假定上述系统从t=0开始活动。设X1=X2= Y1=Y2=0，于第0期设扰动项ε10=0，ε20=0，其他均为0。那么，初期给予的扰动将在系统中不断传递，通过迭代计算可以得到X0，X1，X2,…，称为由X的脉冲引起的Y的响应函数，同样可以求得Y0，Y1，Y2，…，称为由X的脉冲引起的Y的响应函数。当第0期脉冲为ε10=0，ε20=1，可以求得Yt的脉冲引起的X和Y的响应函数。

（4）基于VAR模型的方差分解

方差分解（Variance Decomposition）是将VAR模型中每个外生变量预测误差的方差按其成因分解为与各个内生变量相关联的组成部分，通过分析每一个新息冲击对内生变量变化（通常用方差来度量）的贡献度来评价不同新息冲击的重要性。

随着时间的推移，脉冲响应函数可观察模型中各变量对于冲击的反应，然后根据VMA（∞）的表示形式，提出方差分解方法，定量但是相当粗糙地把握变量间的影响关系。西姆（Sims）依据VMA（∞）的表示形式，提出了定量把握变量间影响关系的方差分解方法：

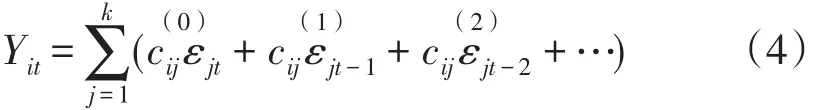
式（4）中各个括号内的是第j个扰动项εj从无限过去直到现在对Yi影响的总和。

2.变量选取与数据说明

由于各变量数据来源及存续期间不同，为了使各变量数据都具有尽可能长的相同时间跨度，本文将研究期间确定为改革开放以来的1978—2012年（因统计资料等原因，未包括我国港、澳、台地区）。因为海南和西藏的历史数据缺失年份较多，为了研究方便，本文如多数相关文献一样在分省市区数据中不包括这两个省区。同时，由于历史数据无法拆分的原故，本文对四川、重庆的数据进行合并，将数据合并后的四川、重庆合称为“川渝”以示区别。因此，基本变量是28个省市区的服务业增长、劳动力投入、资本投入和技术效率。各变量的数据来自《中国国内生产总值核算历史资料（1952—1995）》《中国国内生产总值核算历史资料（1996—2002）》《中国国内生产总值核算历史资料（1952—2004）》《新中国六十年统计资料汇编》及历年《中国统计年鉴》。各变量的定义及数据说明如下：

（1）服务业增长（Y）

即服务业产出，表示历年中国服务业的实际产出，以历年中国各省市区服务业（第三产业）的国内生产总值（GDP）代表相应的服务业产出。为了保持产出数据的可比性，利用各省市区历年第三产业GDP指数（1978年=100）折算出各省市区历年的以1978年不变价计算的GDP。

（2）服务业劳动力投入（L）

表示历年中国服务业的劳动力数量投入，以历年中国服务业从业人员数量代表服务业劳动力投入。

（3）服务业资本投入（K）

表示历年中国服务业的资本投入，以历年中国各省市区服务业的资本存量代表服务业资本投入。由于中国现有统计资料中只有历年资本形成总额的数据，没有资本存量的数据，本文采用永续盘存法对中国各省市区服务业的资本存量进行了测度。

（4）服务业技术效率（TE）

表示中国服务业技术效率，其数据根据服务业产出、服务业劳动力投入、服务业资本投入通过随机前沿分析（SFA）方法计算求得。

三、实证分析

在不改变时间序列数据特征的前提下，为了消除数据中潜在的异方差现象以得到平稳的数据序列，本文对服务业产出、服务业劳动力投入和服务业资本投入的变量序列取自然对数，分别记为LNY、LNL和LNK。继而对服务业技术效率TE、LNY、LNL和LNK取一阶差分，可以推断出LNY、LNL和LNK三个变量可能存在一阶单整。

1.平稳性检验

本文采用ADF检验法对数据进行单位根检验，得到结果如表1所示。可知，ΔTE、LNY、LNL和LNK序列是非平稳序列，而其一阶差分则是平稳序列，因此四者都是一阶单整I（1）序列，满足协整检验的条件。采用约翰森协整检验法，由检验结果可知TE、LNY、LNL和LNK四个变量之间理论上存在着协整关系。

2.向量自回归模型的建立

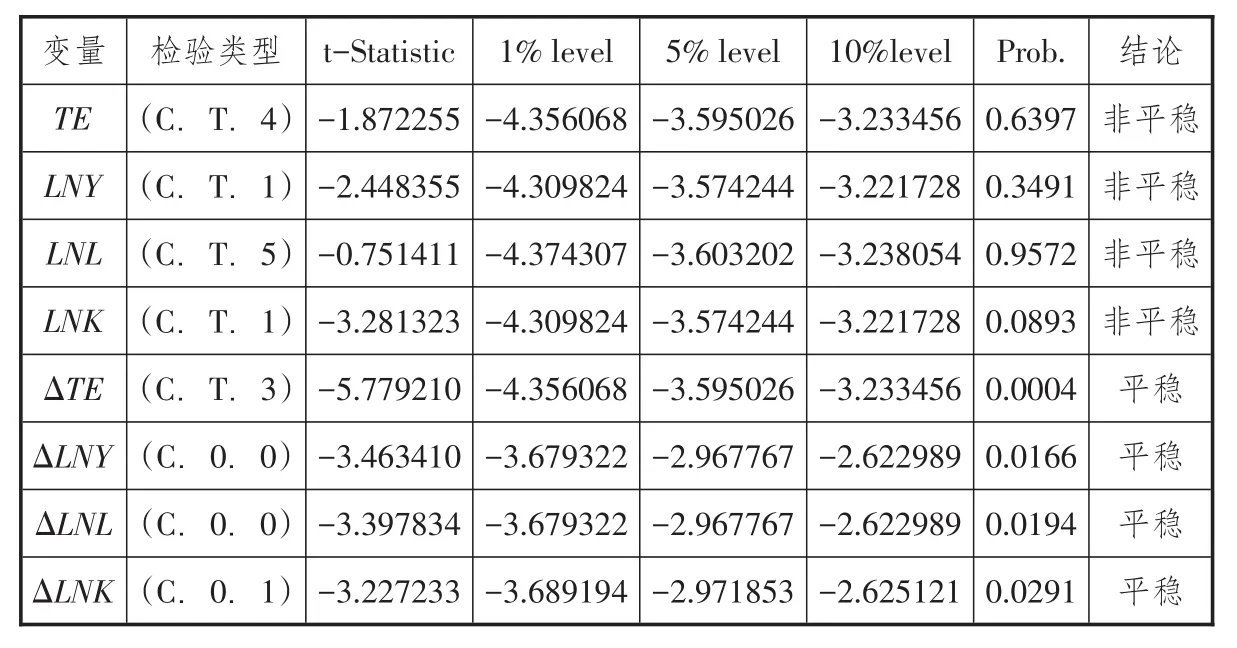
表1 各内生变量的单位根（ADF）检验结果

需要利用向量自回归（VAR）模型进一步对TE、LNY、LNL和LNK之间的系统关系做脉冲响应分析，在（1）式的基础上，以时间序列TE、LNY、LNL和LNK建立VAR模型。准确建立VAR模型的关键是正确确定滞后阶数p。应在滞后期与自由度间寻求一种均衡状态，一般根据AIC和SC信息量取值最小的原则确定模型的阶数。最后确定滞后阶数为5，模型设定为VAR（5），得到估计式如（5）式所示。其中，可决性残差协方差为6.15E-23，对数似然值为603.02，AIC值为-39.92，SC值为-35.86。

3.脉冲响应函数分析

在VAR模型基础上采用脉冲响应函数方法对模型进一步研究，分析TE、LNY、LNL和LNK对各变量脉冲扰动的动态响应及其累计响应。

（1）TE对各变量脉冲扰动的动态响应

第一，TE对自身的一个标准差新息的冲击具有明显的正向响应，所有时期都为正向响应。TE的累计响应为正，表明长期内TE对自身响应有显著的正向影响效应。第二，TE对于LNY的一个标准差新息的冲击具有明显的正向响应，所有时期都为正向响应。在整个观察期内，TE对LNY的一个标准差新息冲击的累计响应为正，表明长期内LNY对TE有正向影响效应。第三，TE对于LNL的一个标准差新息的冲击具有明显的负向响应，在各个时期都为负向响应。整个观察期内，TE对LNL的一个标准差新息冲击的累计响应为负，表明长期内LNL对TE有负向影响效应。第四，TE对LNK的一个标准差新息的冲击具有明显的负向响应，在各个时期都为负向响应。在整个观察期内，TE对LNK的一个标准差新息冲击的累计响应为负，表明长期内LNK对TE有较显著的负向影响效应。

（2）LNY对各变量脉冲扰动的动态响应。第一，LNY对自身的一个标准差新息的冲击在第1期为显著的正向响应，在第2期达到顶峰之后迅速降低，直到第5期转为负向响应，在第7期达到最低值后逐渐回升，整个过程呈现巨大的波动性。LNY对自身的累计响应为正，表明长期内LNY对自身响应有显著的正向影响效应。第二，LNY对TE的一个标准差新息的冲击在第1期便为正向响应，在第2期达到顶峰之后迅速降低，直到第5期转为负向响应，在第7期达到最低值后逐渐回升，整个过程呈现波动性。LNY对TE的累计响应为正，表明长期内TE对LNY响应有正向影响效应。以上分析表明，TE和LNY之间的互相影响具有相似性和同步性，这是因为它们都作为LNL、LNK相互作用的产物，只是表现方式不同。第三，LNY对于LNL的一个标准差新息的冲击在第1期为0，第2期达到正向最大值，之后逐渐降低，在第5期为0，在第6期转为负值，在第7期达到负向最低值后逐渐回升。整个过程呈现出波动性，但LNY对LNL的累计响应为正，表明长期内LNL对LNY响应有正向影响效应。第四，LNY对LNK的一个标准差新息的冲击在第1期为0，在第3期达到正向最大值之后逐渐降低，在第7期为0，在第8期转为负值，在第9期达到负向的最低值后逐渐回升。整个过程呈现出波动性，但LNY对LNK的累计响应为正，表明长期内LNK对LNY响应有正向影响效应。以上分析表明，LNL、LNK对LNY的影响具有相似性，只是LNK的影响比LNL的影响滞后1到2期。

（3）LNL对各变量脉冲扰动的动态响应

第一，LNL对自身的一个标准差新息的冲击立即表现出显著的正向效应，在第1期就达到最大值，之后逐渐衰减，在第5期转为负值，在第7期达到最低值后逐渐回升，整个过程呈现出明显的波动性。但LNL对自身的累计响应为正，表明长期内LNL对自身响应有正向影响效应。第二，LNL对TE的一个标准差冲击在初始期就呈现明显的正效应，在此之后逐渐衰减，直至在第4期变为负值，在第6期达到最低值后开始逐渐回升，并在第8期重新为正值，呈现明显的波动性。但LNL对TE的累计响应为正，表明长期内TE对LNL响应有正向影响效应。第三，LNL对于LNY的一个标准差新息的冲击在初始期就呈现显著的正向效应，在此之后逐渐衰减，直至在第5期变为负值，在第6、第7期达到最低值后开始逐渐回升，并在第9期重新为正值，呈现明显的波动性。但LNL对LNY的累计响应为正，表明长期内LNY对LNL响应有正向影响效应。以上分析表明，TE、LNY对LNL的影响具有相似性，只是LNY的影响比TE的影响滞后1到2期。第四，LNL对LNK的一个标准差新息冲击的响应在初始阶段为0，之后在第3期上升达到最大值，此后逐渐下降，在第6期转为负值，在第8期达到最小值后逐渐回升，呈现明显的波动性。但LNL对LNK的累计响应在前8期在正向效应内波动，在第8期后转为负值并逐渐降低，这表明长期内LNK对LNL的影响有阶段性和波动性，在前8期的影响由0至最大值然后又降至0，此后将转为负向影响效应。

（4）LNK对各变量脉冲扰动的动态响应

第一，LNK对其自身的一个标准差新息冲击的响应大部分时期保持为正效应。从第1期开始一直呈现正向响应并逐渐增加，在第4期达到最大值之后逐渐衰减，到第10期达到最小值并变为负值，整个过程呈现出明显的波动性。但LNK对自身的累计响应为正，表明长期内LNK对自身响应有正向影响效应。第二，LNK对TE的一个标准差冲击在初始期就呈现微弱的正响应，在此之后逐渐衰减并转变为负值，在第7期达到最低值后开始逐渐回升，呈现明显的波动性。LNK对TE的累计响应为负，表明长期内TE对LNK响应有负向影响效应。第三，LNK对于LNY的一个标准差新息的冲击在初始期呈现明显的正向响应，在此之后逐渐衰减并转变为负值，在第8期达到最低值后开始逐渐回升，呈现明显的波动性。LNK对LNY的累计响应先为正后为负，表明长期内LNY对LNK响应有阶段性和波动性。以上分析表明，TE、LNY对LNK的影响具有相似性，只是LNY的影响比TE的影响往往滞后1到2期。第四，LNK对LNL的一个标准差新息冲击的响应在第1期呈现正向响应并逐渐增加，在第2期达到最大值之后逐渐衰减，到第7期转为负值，在第9期达到最小值之后有所回升，整个过程呈现出明显的波动性。但LNK对LNL的累计响应为正，表明长期内LNL对LNK响应有正向影响效应。

4.方差分解

为进一步了解服务业技术效率与产出、劳动力投入、资本投入之间的相互作用的贡献度，对VAR（5）模型做方差分解，结果如表2至表5所示。

（1）TE受各变量的影响

由表2可知，LNY在第1期只受其自身波动的影响，LNY、LNL和LNK的影响（即对预测方差的贡献度）在第2期才显现出来，但其影响强度微乎其微。但是，在随后各期，LNK的影响逐渐增强，在第10期达到最大值28.26%。这说明服务业技术效率主要受自身和资本投入的影响，其中2/3的影响来自自身，近1/3的影响来自服务业资本投入。而服务业产出和劳动力投入对服务业技术效率变化的贡献度很小，可以忽略不计。

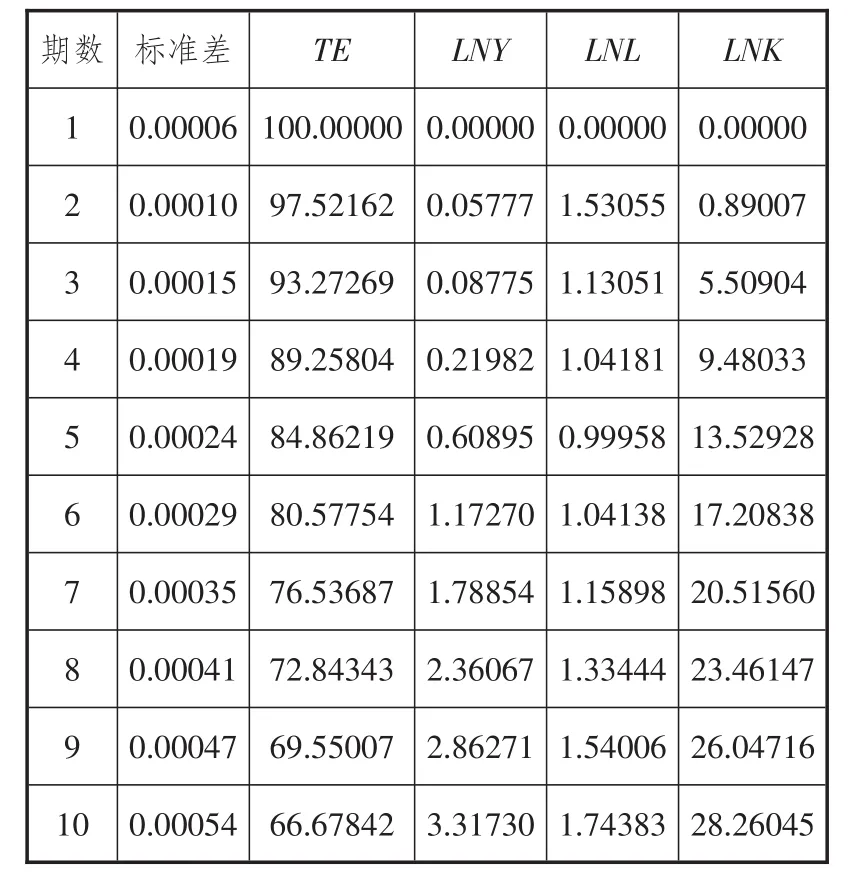
表2 TE的预测方差分解结果

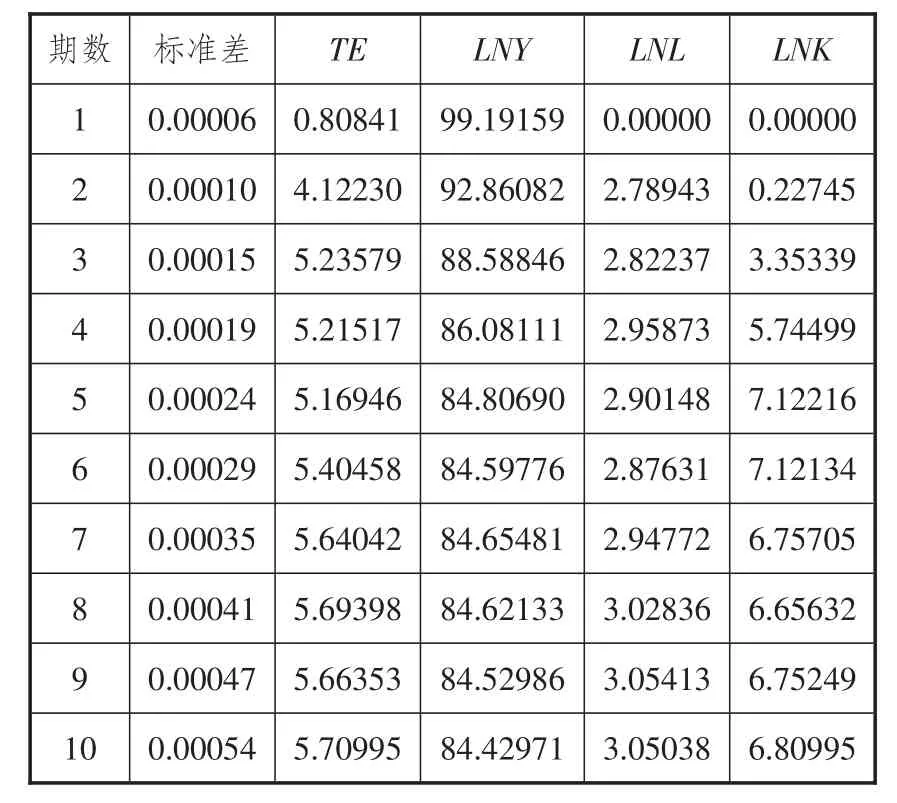
表3 LNY的预测方差分解结果

（2）LNY受各变量的影响

由表3可知，LNY在初期主要受到自身波动的影响（即对预测方差的贡献度）。在第5期之后，LNY所受影响的构成趋于稳定，近85%的影响来自自身的波动，15%的影响来自TE、LNL和LNK的影响，而此时这三者的贡献率也基本保持稳定。这说明服务业产出主要受自身影响，虽然还可能受到服务业技术效率、劳动力投入、资本投入等因素的影响，但通常可以忽略不计。

（3）LNL受各变量的影响

由表4可知，LNL的预测方差主要受其自身及LNY、LNK的影响。其中，LNL自身的影响逐渐衰减，由第1期的46.39%降至第10期的24.37%；TE的影响保持稳定，基本维持在7.26%左右；LNY的影响保持相对稳定，基本保持在45%左右，并逐渐成为最主要的影响因素；LNK的影响由无至有，逐渐增加，由第1期的0增至第10期的25.27%，最后达到与服务业劳动力投入相同的影响程度。以上分析说明服务业劳动力投入主要受自身及服务业产出、服务业资本投入三者影响。

（4）LNK受各变量的影响

由表5可知，LNK主要受自身的影响，同时也受到TE、LNY和LNL的影响。LNK受自身的影响程度在不断降低，由第1期的67.46%降至第10期的44.44%；LNK受TE的影响程度在不断增加，由第1期微不足道的0.42%增至第10期的15.32%； LNK受LNY的影响程度也在不断增加，由第1期的13.66%增至第10期的27.75%；而LNK受LNL的影响程度是先升后降，由第1期的18.45%增至第3期的23.82%，然后又逐渐降低至第10期的12.50%。以上分析说明服务业资本投入主要受自身的影响。

四、研究结论与讨论

本文基于VAR模型，运用脉冲响应函数、方差分解等方法对改革开放30余年（1978—2012）中国服务业技术效率与服务业增长（产出）、劳动力投入、资本投入之间的关系进行了研究。结果表明这四者之间存在着较为稳定的均衡关系，四者之间存在着相互作用和影响，并得到以下结论和启示。

表4 LNL的预测方差分解结果

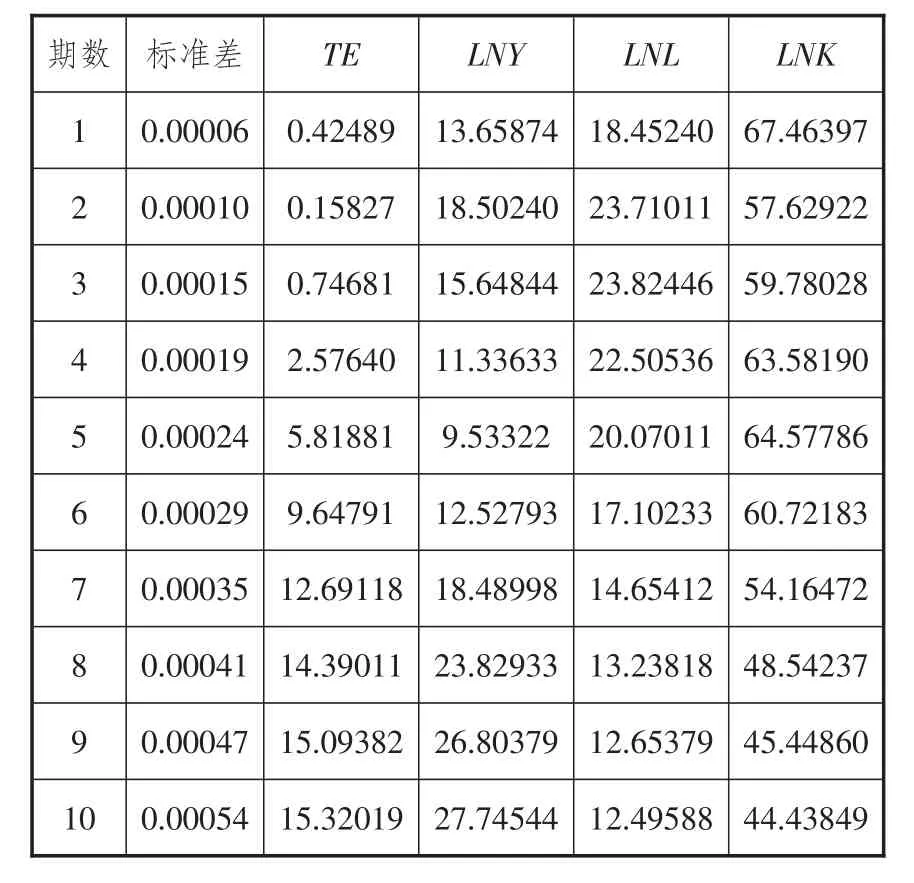
表5 LNK的预测方差分解结果

1.主要结论

（1）服务业技术效率与服务业增长、服务业要素投入之间存在稳定的均衡关系。约翰森协整检验结果以及VAR模型具有较好的拟合度和稳定性，表明服务业的技术效率与增长、要素投入之间存在稳定的均衡关系。

（2）服务业技术效率与服务业增长、服务业要素投入之间存在动态的相互作用机制。脉冲响应函数的分析结果表明服务业技术效率与服务业的增长、劳动力和资本投入之间存在着互相影响的动态关系。长期内，服务业增长对技术效率有正向影响效应，劳动力和资本投入对技术效率有负向影响效应；同时，技术效率的变化也会对服务业增长、劳动力和资本投入产生反作用，这种反作用通过服务业增长、服务业劳动力和资本投入的变化再次传导给技术效率，产生新一轮的变化，如此循环往复。在技术条件不变的情况下，中国各地区服务业的增长、劳动力和资本投入的数量不同而且一直处于变化状态，这必然导致技术效率也产生相应变化，当技术效率的变化逐渐积累并达到一定数量级别时就显现出来，造成地区间服务业技术效率的差异。

（3）服务业增长与要素投入对技术效率影响的贡献率并不相同。方差分解结果表明服务业技术效率受其自身及服务业增长、劳动力和资本投入的影响。此外，服务业技术效率受资本投入的影响（负向）最大，占总影响的近1/3，受服务业增长的影响（正向）其次，受劳动力投入的影响（负向）最小。同时，服务业技术效率对服务业增长、劳动力投入、资本投入也分别有程度不同的反作用。这表明当前应把服务业资本投入当作服务业技术效率最主要的内生影响因素来研究。

2.启示与对策

（1）在提高服务业技术效率过程中应注意各因素之间稳定的均衡关系和动态作用机制。服务业的快速增长在一定程度上可以吸引更多的劳动力和资本投入服务业，但这种吸引作用是有限的，很容易产生投入冗余，进而降低效率。产生的冗余劳动力投入难以转化为价值，并从整体上降低服务业效率；而资本投入的主要用途是支付劳动力成本而非购买物质设备，资本投入对服务业增长也没有显著作用。过度投入会造成投入冗余，反而会降低效率，这是当前中国服务业技术效率普遍存在的问题。

（2）在提高服务业技术效率过程中应调整服务业增长与要素投入的比重。因为这些内生因素对服务业技术效率影响的贡献率并不相同。随着服务业的持续增长，服务业技术效率有逐渐提高的趋势和空间。服务业资本投入是当前服务业技术效率最主要的负向影响因素，资本投入增加无效甚至起到相反作用。因此，当前应逐渐减少对服务业的盲目资本投入，积极调整资本投入领域。服务业劳动力投入是服务业技术效率的负向影响因素。现代服务业是以劳动力素质为基础的知识、技术、创意密集型产业，劳动力数量的简单增加对服务业技术效率的作用是负面的，它将成为提高效率的负担，取而代之的是以劳动力受教育年限为表征的劳动力素质、知识和技能的提高。因此，重点应转变为关注劳动力素质的提高和人力资本投入的增加。当前服务业本身在不断升级换代，以往结构层次较低的劳动密集型服务业逐渐被知识、技术、创意密集型的现代服务业所取代，服务业从业人员的素质也应相应提高。

因此，为了提高服务业的技术效率，有效促进服务业增长，在制定相关政策措施时应考虑以下建议：第一，控制服务业的劳动力和资本投入数量，对冗余投入要不断分解和消化，控制好投入与产出之间的比例。在制定发展服务业的政策时，需要转变服务业发展方式，逐渐改变过去靠要素投入推动服务业发展的方式，转变为依靠提高服务业发展的效率。第二，不断提高劳动者的素质、知识和技能。如在信息化水平不断提高的基础上提高劳动者素质，吸收基于劳动者素质提高而带来的科技进步成果，这都将进一步促进服务业增长，进而改善产业结构。

＊本文系陕西省教育厅专项科研计划项目“陕西生产性服务业集聚及其对创新能力的影响研究”（项目编号：2013JK0112）、陕西省软科学项目“陕西生产性服务业集聚与协同创新的互动机制研究”（项目编号：2014KRM25）、陕西省高校哲学社会科学重点研究基地科研计划项目“生产性服务贸易对陕西制造业竞争力的影响研究”（项目编号：14JZ017）、陕西省社科界重大理论与现实问题研究项目“陕西生产性服务业与制造业互动发展研究”（项目编号：2015C053）、陕西省普通高校哲学社会科学特色学科建设项目“陕西纺织经济管理研究中心”资助项目、西安工程大学博士科研启动基金资助项目“中国区域服务业技术效率的时空变动及其影响机制研究”（项目编号：BS1423）的部分研究成果。

[1]顾乃华，李江帆.中国服务业技术效率区域差异的实证分析[J].经济研究，2006（1）：46-56.

[2]顾乃华.我国服务业发展的效率特征及其影响因素——基于DEA方法的实证研究[J].财贸研究，2008（4）：60-67.

[3]任英华，王耀中.国际服务业生产率的发展趋势及影响因素分析[J].统计与信息论坛，2008（9）：59-64.

[4]杨青青，苏秦，尹琳琳.我国服务业生产率及其影响因素分析——基于随机前沿生产函数的实证研究[J].数量经济技术经济研究，2009（12）：46-57.

[5]徐盈之，赵玥.中国信息服务业全要素生产率变动的区域差异与趋同分析[J].数量经济技术经济研究，2009（10）：49-60.

[6]谷彬.中国服务业技术效率测算与影响因素实证研究——来自历史数据修订的史实证据[J].统计研究，2009（8）：63-70.

[7]黄莉芳，黄良文，洪琳琳.基于随机前沿模型的中国生产性服务业技术效率测算及影响因素探讨[J].数量经济技术经济研究，2011（6）：120-132.

[8]许建平，任燕.我国服务业效率特征研究——基于区域发展差异影响因素的解释[J].产业经济研究，2012（1）：70-77.

[9]刘中艳.现代服务业技术效率区域差异及成因——基于省际面板数据的分析[J].江西社会科学，2013（8）：81-85.

[10]邵金菊，王培.中国软件服务业投入产出效率及影响因素实证分析[J].管理世界，2013（7）：176-177.

[11]殷凤，张云翼.中国服务业技术效率测度及影响因素研究[J].世界经济研究，2014（2）：75-80.

责任编辑：方程

Analysis of the Dynam ic Relationship among Growth，Input of Elements and Technological Efficiency of Chinese Service Industry

WANG Tieshan1，2
（1.Xi’an Polytechnic University，Xi’an，Shannxi710048，China；2.Xi’an Technology University，Xi’an，Shannxi710032，China）

Based on the VARmodel，impulse response function，and variance decompositionmethod，the author carriesout a study on the relationship among growth，the inputof labor and capital，and technologicalefficiency of China’s service industry since reform and opening up(from 1978 to 2012).It shows that the growth in service industry has the positive effect on technologicalefficiency；input in labor and capitalof service industry has the negative effecton technologicalefficiency；and the accumulation of these dynamic effects is the intrinsic cause for the formation of the current situation and regional difference of technologicalefficiency of China’sservice industry.

service industry；technologicalefficiency；impulse response function

F719

A

1007-8266（2015）08-0081-08

王铁山（1974—），男，河北省唐山市人，西安工程大学管理学院高级经济师，博士，西安工业大学经济管理学院特聘教授，主要研究方向为产业经济、技术经济。