基于SPAMS和GPCA的人脸识别算法的研究

2015-01-06田小敏南京工业职业技术学院计算机与软件学院

大陆桥视野 2015年22期

田小敏/南京工业职业技术学院计算机与软件学院

田小敏/南京工业职业技术学院计算机与软件学院

人脸识别是近年来模式识别图像处理,机器视觉,神经网络以及认知科学等诸多领域的热点课题之一,本文主要是基于GPCA（广义主成分分析方法），对经传感器采集得到的一系列尺寸相同的人脸图像进行识别研究以及理论探讨。针对常用人脸识别方法的弊端和不易操作性，运用SPAMS 工具包（Sparse Modeling Software toolbox），研究图像的降维稀疏表示。

人脸识别；广义主成分分析；稀疏表示

1. 引言

随着安全入口控制和金融贸易方面应用需要的快速增长以及各方面对于快速有效的自动身份验证的迫切要求，生物统计识别技术得到了新的重视，而人脸识别是所有的生物识别方法中应用最广泛的技术之一，目前国内外研究也取得了一定的进展，综合有关文献[1][2]，目前国外人脸识别的方法主要集中在以下几个方面：

(1) 模板匹配的方法

(2) 示例学习的方法

(3) 神经网络的方法

(4) 基于隐马尔可夫模型的方法

除此以外，基于Ada Boost的人脸识别算法，基于彩色信息的方法，基于形状分析的方法，以及多模态信息融合的方法，国外都进行了大量的研究与实验。

国内的研究工作主要是集中在三大类方法的研究：基于几何特征的人脸正面自动识别方法、基于代数特征的人脸正面自动识别方法和基于连接机制的人脸正面自动识别方法。

总之，采用人脸识别技术，建立自动人脸识别系统，用计算机实现对人脸图像的自动识别有着广阔的应用领域和诱人的应用前景。

在上述研究基础上，本文主要对基于广义主成分分析的人脸识别算法进行研究，并结合在SPAMS工具包下对图像进行稀疏处理，其中稀疏表示是特色。主要内容是信号稀疏表示以及matlab稀疏工具包SPAMS的简要介绍和应用，包括识别过程中所需要的基本图像处理技术，并阐述在此基础上和GPCA技术结合的人脸识别算法流程。

2. 基于SPAMS图像稀疏表示

每个大小为w×h 的图像可看作M维空间的一个点，M=w×h，同一个面孔的不同亮度和表情被表示到M维空间中的低维线性子空间，称为脸子空间。

我们定义ni个图片，向量vi,1，vi,2，…，vi,ni∈Rm并假设这些向量足以包含i系列的脸子空间，任何关于相同目标的新的训练图像，即为向量y∈Rm，y可以表示如下：

其中αi,1是实标量，将所有ni相加得n=n1+n2+…+nk,作为向量A的n列：

理想的y（关于i）可以用A表示为：

其中：x0=[0, …,0,αi,1, αi,2, …, αi,n,0, …,0]T∈Rn(列向量)。X0是一个系数矩阵，其元素几乎是0，处理与i系列有关系的元素。我们得出如下简单的意见：一个有效地测试图像可以只用有相同变量的测试图像群充分表示出。如果变量的数目k大得合理，表示是自然稀疏的。

x0是一个系数矩阵，其元素几乎是0，处理与i系列有关系的元素。我们得出如下简单的意见：一个有效地测试图像可以只用有相同变量的测试图像群充分表示出。如果变量的数目k大得合理，表示是自然稀疏的。

如果system3(under-determined)(m＜n且A∈Rm×n)，它的答案不唯一。通常解决办法由最小二乘法来选择。即：

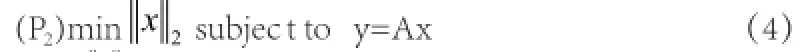
类似的，如果system3(over-determined)(m＞n)，通常通过最小化找到最小二乘法解决办法。然而，这种方法不能定位识别问题中的如下两种重要性质。

1）数据维数很高。

2）理想的解答是稀疏的：x0中非0元素所占比例只是

为了解决上面的问题，我们寻找的方法能够：(1)使维数m降低到d 且d≤m ；(2)明确计算y在低维空间中的稀疏矩阵表示。如果这两个目标都能完成，我们将会看到适当的加强稀疏可以使结果更少地依赖于维数低的细节（过程）。

在数据库里，大维数缩减方法常被用于映射高维人脸图像到低维特征空间，已有一类方法能提取所有面部特征，例如特征脸方法，费舍尔脸方法等，从图像空间到特征空间的映射可以表示为：矩阵将等式(3)两边同乘以R可得：

映射后，特征空间的维数d通常比n小。因此，等式(5)所表示的系统是under-determined，x的解也不是唯一的。然而，理想中的x0应该是稀疏的，在不严格的条件下系统的方程的最稀疏解确实是唯一的。也就是说，理想中的x0是如下最优化问题的唯一解：

解决（P0）是NP-hard ，而且很难通过多项式时间算法去近似求解。在通常情况下，无疑通过程序来寻找最稀疏解比费力的找x中元素的所有子集有效。

压缩传感理论的最近发展揭示了如果解x0是充分稀疏的，相关的（P0）问题等价于求一下的L1最小化问题：

这个问题能通过标准线性多项式时间程序或者二次多项式程序方法来解决。如果已知道解是很稀疏的，那么更有效的方法也是可考的。

3.GPCA人脸识别算法

传统的广义主成分分析法一般不包含稀疏表示部分，不适用SPAMS工具包，具体识别流程如图2所示。

图2 传统的广义主成分分析法识别流程

本文通过改进，采用广义主成分分析方法，并结合图像的稀疏表示，使用SPAMS工具包，具体的流程设计如图3所示：

图3 改进后算法的识别流程

对各个部分介绍如下：

(1)人脸图像采集：基于CMOS图像传感器成本低、功耗低、单一工作电压、集成 AD 转换器、数字形式数据输出、图像大可编程控制等优点,可以使用CMOS图像传感器，如MT9T001 CMOS图像传感器。这里由于软硬件条件限制，直接使用yale人脸库中的标准图像。

(2)读取图像数据：直接调用matlab里面imread函数，将图像以矩阵的形式体现出来，我们知道，通常通过传感器采集到的图像是彩色的，彩色有三种基色组成，red，green，blue；graycolor = (Red + Green + Blue)/3，简称RGB，彩色图像是三维的，可以通过简单的行列操作得到一维（一种基色下的）图像，再进行相关的处理。如果图片的尺寸过于大，可以用imresize函数进行调整。这里将训练集的图像矩阵信息降维到一个矩阵里面，每一列代表一个图像信息。

(3)特征脸定位：每个人脸图像有个特征矩阵代表它的信息，同理也可以通过矩阵处理得出均值脸图像。这里可以通过每个图像矩阵减去特征矩阵得到特征矩阵A（但不能完整表达出一幅图像），根据广义主成分分析理论，求出AAT的特征向量就能表达出图像信息，当然这中间包括一些细节操作，如规范化等等。若想得出特征脸图像可以通过imshow函数来画。

(4)SPAMS工具包L1范数最小化求解：调用SPAMS中的mexOMP函数来求解L1范数最小化问题。这里调用的格式是A=mexOMP(y,S,param); y是测试图像矩阵，S是训练集图像矩阵，param对应下面的γ，得出的矩阵A是稀疏解，这里S是已经经过规范化处理之后的矩阵，每一个测试图像对应一个稀疏解，故所有的测试图像可以以解集{A1,A2,…，Ai}的形式代表出来，达到了降维的目的，使计算量减少了很多。

(5)重构图像及对比：这里可以通过y=AS来恢复测试图像，当然过程中会涉及矩阵的反规范化处理，以正确求解。同样可以将原始图像和重构图像在matlab中画出，以便对比分析。这里面图像的恢复程度依赖于γ的取值，直接调用的mexOMP函数，param的取值也依赖于它的形式规定和读者自己设定。

(6)识别率计算：文献中给出传统的识别判别方法是NS和NN方法，NS分类法：如果y到子空间（包括主体i的所有图片）的距离就把测试图片y分配给主体i：