直线式多站台公交车站交通流特性的研究

梁玉娟 韦兰香 邓卫娟 唐秀福/河池学院物理与机电工程学院

直线式多站台公交车站交通流特性的研究

梁玉娟 韦兰香 邓卫娟 唐秀福/河池学院物理与机电工程学院

基于元胞自动机NaSch 交通流模型，提出了直线式多站台公交车站设置的双车道元胞自动机交通流模型，计算机数值模拟结果表明：在周期边界条件下，直线式多站台公交车站的设置对交通流有较大的影响，但不同停泊车位数对应的车流量没有按照一定的趋势变化，且站台长度对交通流的影响情况没有公交车占有比例对交通流影响那么明显。

元胞自动机；直线式；多站台公交车站；双车道

公交车中途停靠站是城市最基础的公交设施，几乎分布在城市任何一条有公交车辆运行的道路上，虽然只占城市道路很短的一段，但对路段通行能力影响却很大，是交通拥堵常发地段。在城市的中心区或老城区，由于建设年代早，道路宽度较窄，难以设置港湾式中途停靠站，多数是沿路侧设置直线式中途停靠站，且不同线路公交车停靠常设置在同一站点。公交车站停靠能力是反映公交车站能提供公交车停靠服务能力大小的指标，是公交基础设施提供公交服务的最大供应量，它受停靠站的停车区域长度的限制[1,3]，如果站台过短，就不能发挥公交车停靠站的作用，反而会影响道路的通畅；相反，站台过长，不仅会浪费道路资源，还不利于车辆的有序停靠，不方便乘客的上下车[2-3]。合理的站长既能充分利用道路的交通设施，又能满足对公交服务的要求，同时又能减轻停靠站附近环境的污染[3]。关于公交车站对交通流的影响已有许多学者对其关注[3-9]，而关于数值模拟研究站台长度对交通流的影响却较少见，本文应用NaSch模型数值模拟不同站台长度对交通流的影响情况。

1.模型与规则[3-5]

本文只研究直线式公交车站点，经过同一路段的所有线路公交车都集中在同一个站点在车道上进站停靠。一般道路系统都是由多条车道组成，为简化问题，采用双车道模型，如图1所示。

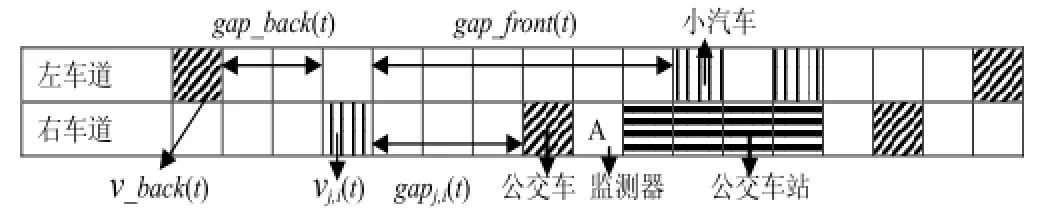
图1 直线式公交车停靠站的双车道模型

将城市道路看作是左右两条并列的、含有L个格点（cell）的一维离散格点链，这里长度均以格点为单位，做无量纲化处理。对应实际道路长为7.5m的每个格点每一时刻或被一辆车占据或为空。假设道路上只有公交车和小汽车，并不计车辆长度。公交车站设在道路的中部，小汽车、公交车、公交车站分别用不同条纹的格点表示。A为统计流量的监测器，设在公交车站之前。考虑到车辆的加速、减速过程，建模时引入了随机慢化的概率，用车速v表示车辆的状态，v允许在{0,1,2，…，vmax}范围内取值，vmax为最大车速。公交车体积大，速度小，取vmax=2cell/s=54km/h；小汽车虽然体积小，速度大，但市内交通拥挤，取vmax=4cell/s=108km/h。左车道为快车道，右车道为慢车道且设置有公交车站点，因此，慢车道按公交车比例f=0.1随机混合地分布小汽车和公交车，而快车道只随机分布一种小汽车，车辆一旦分布到车道上，令其立即获得一个v∈[0，vmax]的车速。设车辆从左到右，可变换车道在两条车道上循环行驶，并设两种车辆具有相同的随机慢化概率p=0.25。公交车辆在公交车站处不允许超车，实行先到先进站先行的原则，而车辆状态演化的更新规则、公交车站处小汽车运行规则、车辆换道规则均与文献[3-5]的一致。

2.数值模拟与分析

图2 公交车比例f=0.1时的基本图：（a）为左车道；（b）为右车道

图2表明：①公交车比例较小时，两车道的流量都比较大，因为车道上主要是速度较大的小汽车，公交车后面的小汽车可以通过换道行驶，公交车站的“瓶颈”限制作用较弱。②左车道的流量比右车道的大，当车流密度时两车道对应的流量都最大，两个最大值之差为0.3073，这主要是由于右车道设有公交车站，公交车是占道停靠服务，其后的公交车需等待停靠，而小汽车则寻找时机转到左车道上，因而左车道上主要是速度较大的小汽车，而右车道主要是速度较小的公交车。③密度很小或者很大时不同停泊车位数对应的流量几乎重合在一起，随密度呈线性增大或线性减小，因为低密度时，车辆相互干扰小能自由行驶，流量主要由车速决定；而高密度时，车辆间相互作用非常大，车速都很小，公交车站对车流的影响减弱，流量主要由密度决定。④中等密度区域出现一个近似平台的流量区域，因为f较小，车辆还能保持相对较大的车速，在遇到公交车进站占道停靠时，其上游的公交车、小汽车或减速或转道，出现时停时走的交通现象。⑤中等密度区域，N=5对应的流量最小，N=2对应的流量最大，N=1、6对应的流量较小，与N=4的接近，介于最小最大值之间，同一密度对应最大流量与最小流量的差值很小，在0.1以下。流量随着N的增多没有按照某一种趋势变化，这是与公交车站的停靠能力有关，而停靠能力除了与站台长度、停靠时间有关外，还受公交车到达率和路段交通状况等因素的影响[2]。N=1，在公交车较多的情况下，公交车相继到达车站，后面到达的公交车要排队等候进站；N=6，相邻两辆公交车到达车站有一定的时间间隔，当最前方的公交车停靠服务完毕离开时，紧跟其后的公交车又未服务完毕，车站处公交车又不能超车，那么后面到达的公交车也只能在后面排队等候，这两种情况公交车站的“瓶颈”作用时间增大，因而对应的流量相应较小。

图3、图4是公交车比例f=0.1，公交车站点及其前后200个格点对应不同停泊车位时两车道的时空演化斑图。横轴表示位置，纵轴表示时间，黑点表示有车辆占据格点，白点表示格点为空，不连续的黑点则表示从相邻车道换道过来的车辆。图中白色区域是道路的间隙；明显的黑色区域是车辆局部拥堵状态；灰色区域是车辆畅通行驶状态。由斑图可知，①N=2、3时，公交站点及其上游路段有比较大的阻塞区域；②N=1、4、5、6时，公交站点及上游路段出现了不连续的拥堵区域，且向上游方向传播，表明车站前（上游方向）出现了时走时停的交通波现象；③车站后面（下游方向）阻塞逐渐消散，但右车道白色区域比较多，表明邻道的小汽车未能急时换道过来；④左车道的车辆密度大，车站下游，白色区域很少，道路利用率高，阻塞消散得迅速，处于自由流状态。斑图也同样能说明基本图的变化趋势。

图3 公交车比例f=0.1，车流密度ρ=0.15，不同停泊车位时左车道的时空演化斑图

图4 公交车比例f=0.1, 车流密度ρ=0.15，不同停泊车位时右车道的时空演化斑图

3.结论

直线式公交车停靠站，公交车辆是占道停靠服务的，此时双车道变成一条车道，显然公交车站成了道路的瓶颈，是造成交通拥堵的重要因素，但车辆可以转道、超车，在一定程度上又可以缓解排队拥堵现象。模拟结果表明：直线式多站台公交车站对交通有较大影响，但车流量没有随着停泊车位数的增加而按照一定的趋势变化，在公交车比例为0.1的条件下，N=2时通行能力最大，N=5时通行能力最小，N=1、4、6通行能力接近，介于最小最大值之间，同一密度对应最大流量与最小流量之差在0.1以下，与文献[3-5]比较，站台长度没有公交车占有比例对交通的影响那么明显。

[1]何宁,马健霄,李娜.公交车站停靠能力的研究[J].城市轨道交通研究,2004，2:78-80.

[2]李娜,陈学武.公交车中途停靠站停靠能力及设计站长计算初探[J].土木工程学报,2003，36(7):72-77.

[3]梁玉娟.公交车停靠对城市道路交通的影响[D].广西大学,2009.

[4]梁玉娟,薛郁.非港湾式公交车站停靠特性的研究[J].力学学报,2012，44(1):111-116.

[5]梁玉娟,盘佳秀,薛郁.公交车站及停靠时间对混合交通流的影响[J].广西物理,2009，30(1):8-12.

[6]郭四玲,韦艳芳,时伟,等．公交车停靠时间的统计分析[J].广西师范大学学报(自然科学版),2006，24(2):5-9.

[7]汪海龙,钱勇生.基于元胞自动机的港湾公交站间距影响研究[J].计算机应用,2007，27(11):2632-2633,2651.

[8]康三军,薛郁.直线式公交车站站点设置的研究[J].力学学报,2012，44(4):718-726.

[9]Zhao XM, Gao ZY, Jia B. The capacity drop caused by the combined effect of the intersection and the bus stop in a CA model[J]. Physica A,2007,385: 645-658.

广西高校重点科学技术项目（2013ZD059）；广西高校优秀人才资助计划项目（桂教人[2011]40号）； 河池学院重点科研项目（2012YBZ-N006）。