基于ANSYS的细长轴车削加工屈曲分析

刘 芳，安向东，张素香

(中原工学院机电学院，河南郑州450007)

0 引言

细长轴作为机械零件中重要的轴类零件，由于其长径比大于20，导致其刚性差，在车削加工过程中难以满足精度要求，一直以来成为机械加工行业中的一大难题。细长轴类零件属于细长杆件，在车削加工过程中，如果受到的轴向力过大，那么工件可能会由于被压弯导致失稳，难以满足加工精度的要求。因此，为了确保细长轴的加工精度，对细长轴车削加工进行屈曲分析，为细长轴车削加工提供理论依据。

1 细长轴在进给力作用下的弯曲模型

考虑到细长轴的实际车削加工情况，建立细长轴车削加工示意图，如图1所示:

图1 细长轴车削加工示意图

细长轴在车削加工过程中由于受到进给力的作用，可能会由于细长轴被压弯而导致失稳，根据实际车削加工情况，建立如图2所示的细长轴在进给力作用下的弯曲模型，并对其约束进行如下优化:三角卡盘简化为固定端限制全部自由度，顶针端简化为铰支端限制z轴向自由度。图中为细长轴的长度，为细长轴的挠度，为细长轴所受的进给力，为B端所受的支反力。

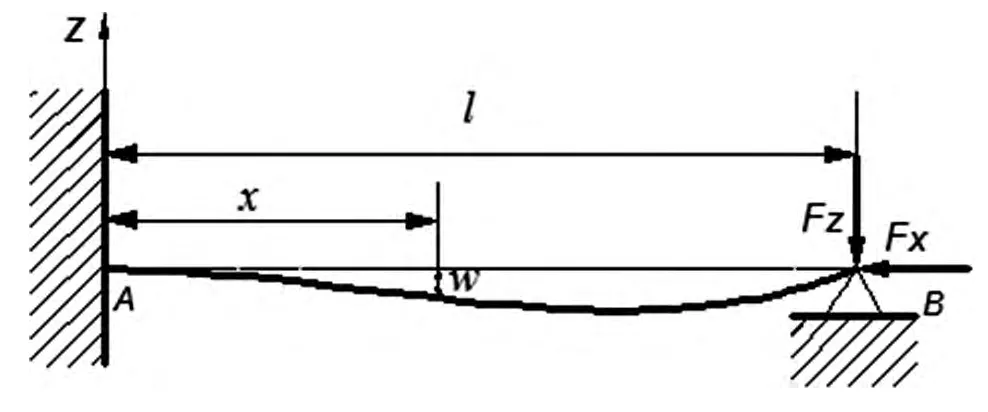
图2 细长轴在进给力作用下的弯曲模型

由材料力学知识可得细长轴在进给力作用下弯曲模型的挠曲线微分方程为:

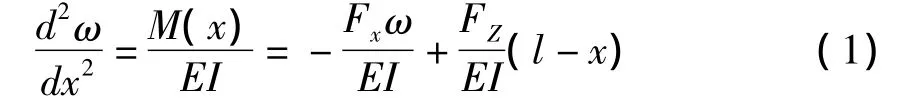
上式微分方程的通解为:

求得ω的一阶导数为:

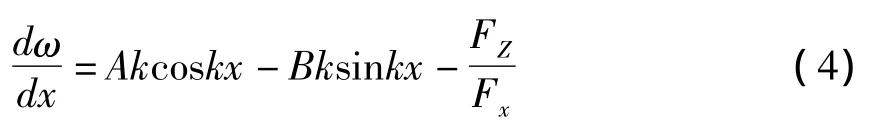
由此可得细长轴失稳的临界力为:

2 非线性屈曲分析

2.1 有限元模型的建立

本节利用有限元仿真软件ANSYS对细长轴车削加工时进给力对车削稳定性的影响做屈曲分析，首先对细长轴进行网格划分，如图3所示。细长轴车削模型是基于梁理论而建立的简支梁模型，综合考虑各种因素的影响，本次仿真采用 Beam188单元。

图3 有限元网格模型

2.2 线性和非线性屈曲分析

特征值屈曲分析属于对理想弹性结构的线性分析的预测，由于在计算过程中将屈曲问题简化，不能准确说明工件发生屈曲的路径，因此实际生产过程中我们将特征值屈曲分析用来估算工件的屈曲极限载荷。但是，又因为特征值屈曲分析能够预测工件的临界极限力，所以在进行非线性屈曲分析之前先做特征值屈曲分析，其结果用来为非线性屈曲分析提供依据。

本节运用ANSYS软件研究细长轴车削加工时进给力对工件弯曲变形的影响，所选用工件仿真参数为:材料选用45钢，长 l=1000mm，直径 d=50mm，密度为7.8g/cm3，泊松比为0.3，弹性模量为2.4e11Pa，背吃刀量为2mm，进给力为518N。由于细长轴属于中性柔度杆件，根据公式(5)可计算得出Pcr=656KN。在仿真过程中假设刀具不受磨损，并且力的大小不变。在仿真时先对工件进行特征值屈曲分析，然后运用所得结果用载荷增量法对工件进行非线性屈曲分析。本节所做的屈曲分析属于大变形分析。为增强迭代求解的精度，需要激活Beam单元的切向刚度矩阵。在求解完成以后，在时间历程后处理器中绘制载荷—位移曲线，仿真结果如图4所示。

图4 仿真特征值载荷

由图4可得细长轴车削特征值屈曲载荷，比理论值偏小，这是由于细长轴在车削时有径向力的作用，所以更容易发生屈曲现象。为了使得到的屈曲载荷更加准确，接下来进行非线性分析，在一阶模态情况下查看细长轴在 Z轴向的变形，如图5所示。

图5 细长轴车削弯曲变形

图5为细长轴车削在一阶特征值载荷作用下的一阶模态位移变形图，从图中可以看出细长轴在车削过程中的最大位移变形发生在中部位置。根据图5所示，把细长轴中间的弯曲变形量作为横坐标，纵坐标为施加载荷的大小，绘制位移载荷曲线，如图6所示。

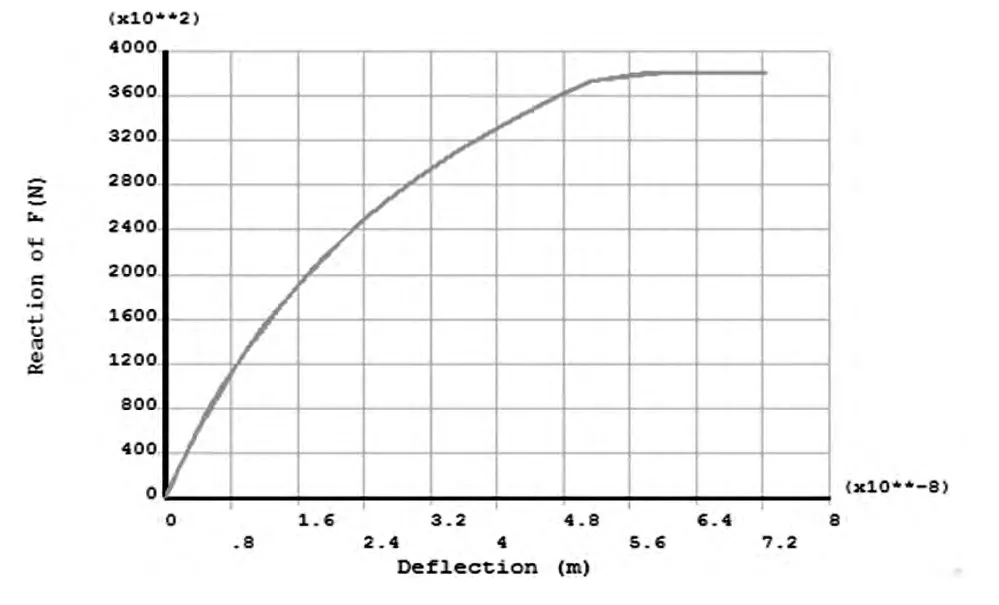
图6 位移载荷曲线

从仿真结果可以得出，细长轴车削加工的非线性屈曲分析极限载荷约为380KN，比理论计算的结果要小很多，因此在细长轴车削加工过程中需要采取辅助支撑，比如跟刀架的使用，这样可以减小细长轴车削加工的弯曲变形，来满足使用要求。

3 结论

通过对比细长轴车削加工模型的理论屈曲极限载荷和有限元非线性屈曲极限载荷，得出了在不采取辅助工具车削加工细长轴的情况下容易产生弯曲变形，即细长轴类工件易出现失稳现象。因此提出在车削加工细长轴的过程中采用跟刀架来保证细长轴的车削加工精度，另外也可以采用双刀车削加工的方法，因为双刀车削加工可以提供径向支撑力来减小轴类工件的弯曲变形。

［1］李玉玲，李志峰，魏伟锋.车削加工细长轴的理论误差分析［J］.煤矿机械，2008，29(10):108—109.

［2］刘龙田.用进刀量补偿法减小细长轴车削加工误差［J］.电子设计与工程，2012，20(21):100 －102.

［3］王小翠，李蔚，侯志敏.细长轴车削用量优化与加工变形误差补偿技术的研究［J］.制造技术与机床，2007(10):85－88.

［4］刘鸿文.材料力学［M］.北京:高等教育出版社，2004.

［5］陈艳霞，林金宝.ANSYS14完全自学一本通［M］.北京:电子工业出版社，2013.