基于新颖蚁群算法的加工中心组成问题研究*

吕聪颖

(南阳理工学院计算机与信息工程学院，河南 南阳 473000)

基于新颖蚁群算法的加工中心组成问题研究*

吕聪颖

(南阳理工学院计算机与信息工程学院，河南 南阳 473000)

针对蚁群算法求解加工中心组成问题易陷入早熟收敛状态的缺点,提出了将听觉信号、记忆矩阵与蚁群算法相融合的一种新颖蚁群算法。在仿真实验中，分别采用蚁群算法、加入听觉信号的蚁群算法、加入记忆矩阵的蚁群算法和新颖蚁群算法对加工中心组成问题进行求解。实验结果表明，新颖蚁群算法能够有效提高蚁群算法的全局寻优能力，收敛速度快，且所求得的组功效优于以上三个策略及以往的混合遗传算法。

新颖蚁群算法；信息素；听觉信号；记忆矩阵

1 引言

加工中心组成问题CF(Cell Formation)[1]是在成组技术的指导下对m台机器进行组织，根据机器之间的相似系数来形成加工中心，从而提高生产的标准化、专业化和自动化程度，进而获得最大的经济效益。

蚁群算法[2,3]以正反馈及分布式计算的特点，在CF问题的求解中获得了广泛应用，但种种研究表明[4～11]，该算法在求解CF问题时易陷入早熟收敛状态。为此，本文结合CF问题，提出了听觉信号、记忆矩阵与蚁群算法相融合的一种新颖蚁群算法NACA(Novel Ant Colony Algorithm)。听觉信号的引入使得精英个体对整个种群的指导作用得以发挥，记忆矩阵的建立使得蚂蚁不断积累自身经验和社会经验，从而更有效地进行搜索。以往文献中未出现这两个策略。

2 加工中心组成问题的数学模型

2.1 问题描述

设有m台机器要组成若干个加工中心，每个加工中心最多可有q台机器、最少p台机器，有n种工件要在这些机器上加工，已知工件和机器的关系矩阵A=[aij]n*m,如果工件j需要在机器i加工，则aij=1，否则为0。

问：如何组成加工中心，才能使总的各中心的机器相似性最大？

2.2 模型的建立

(1)相关参数。

k表示加工中心；Ncell表示加工中心总数，Ncellmin≤Ncell≤Ncellmax,且Ncellmin=[m/q],Ncellmax=[m/p]。

另外，加工中心按自然数从1开始进行编号，即加工中心1,加工中心2,加工中心3,…,显然，最后一个加工中心的编号应为Ncell。

Sij表示机器i和机器j的相似系数(i,j=1,2,…,m),则:

Sij∈[0,1],且

其中，ngij为需在机器i和j上加工的工件数量；ngi为需在机器i上加工的工件数量。

(2)决策变量。

(3)成组技术中加工中心组成问题的数学模型。

目标函数：

(1)

约束条件：

(2)

(3)

yik,yk=0或1，∀i,k

(4)

目标函数式(1)是使成组的相似性最大化，即期望将所有相似的机器指定在同一个加工中心；式(2)用来保证一台机器只能指定在一个加工中心；式(3)用来保证每个中心的机器数不大于其最大容量q且不小于其最小容量p；式(4)为决策变量。

3 基于新颖蚁群算法的加工中心组成问题

在构建算法之前，首先做出如下定义：

设搜索空间维度为m(即机器台数)，种群数目为N，当前迭代次数为t，总迭代次数为gen。

3.1 信息素的表示和更新

采用矩阵L来表示信息素：

其中，ljk(1≤j≤m,1≤k≤Ncellmax)表示将机器j指定在加工中心k所产生的信息素值。

迭代过程中，每只蚂蚁完成搜索后需对信息素进行更新。针对蚂蚁i(1≤i≤N),对信息素的更新公式定义为：

ljk(t)=(1-ρ)ljk(t-1)+γF(xi)

(5)

其中，ρ为控制信息素值的参数；γ为信息素增加常数；F(xi)为蚂蚁i搜索到的解所对应的适应度值(即目标函数值)。

3.2 听觉信号的形成和处理

文献[12]指出，蚂蚁有两种发声方法，即靠叩击或敲打物体发声和摩擦发声，发声的功能之一是召唤同伴。叩击发声的声频最大值可达4 kHz～5 kHZ,摩擦发声的声频为1 kHz～4 kHz。

在此，为了加快算法的收敛速度，选取每一代适应度最高的个体作为精英个体，记为Elite(1≤Elite≤N)。当Elite发现优良食物源时，将对整个种群发出声音信号，以此召唤其它蚂蚁。

根据文献[13]所述的听觉信息传输通路，分两个阶段来模拟听觉的形成。

第一阶段：听觉反馈，模拟听觉信号的形成。

定义2蚂蚁i与Elite的差异度为：

i∈{1,2,…,N}

(6)

文献[14]指出，对于800 Hz以上的频率，听觉信号完全满足对数频率。为此，听觉信号产生公式定义为：

(7)

那么，蚂蚁i从该听觉信号中获得的启发信息究竟有多少呢？

第二阶段：听觉信号的处理，模拟大脑皮层的听觉中枢接收和理解听觉信号的过程，见式(8)：

(8)

3.3 记忆性

对于加工中心组成问题，定义蚂蚁i(1≤i≤N)的记忆矩阵如下：

步骤1如果蚂蚁i在第t代获得的解优于第t-1代，则根据当前位置向量xi=(xi1,xi2,…,xim)来更新记忆矩阵，设蚂蚁i的自身经验积累强度为α(α>1)。如果xij=k(1≤j≤m；1≤k≤Ncellmax)，则令:

(9)

步骤2设第t代的最优解所对应的位置向量为X=(X1,X2,…,Xm),蚂蚁i的社会经验积累强度为β(β>1)。如果Xj=k(1≤j≤m；1≤k≤Ncellmax),则令:

(10)

其中，α和β采用异步时变的方法设置：

es=esstart-t×(esstart-esend)/gen,es=α,β

(11)

开始时，设置α较大，β较小，这样可使蚂蚁倾向于搜索整个空间；后期则相反，可使蚂蚁倾向于搜索全局最优解。

3.4 概率选择公式

(12)

根据公式(12)可得蚂蚁i的概率选择矩阵Pi：

3.5 可行解的获得

概率矩阵表明加工中心问题的潜在解，对矩阵进行解码可得加工中心组成问题的解。

首先，针对蚂蚁i，定义数组b[Ncellmax+1]来记录指定于每个加工中心的机器数目(b[k]记录指定于加工中心k的机器数目)，初始均为0。

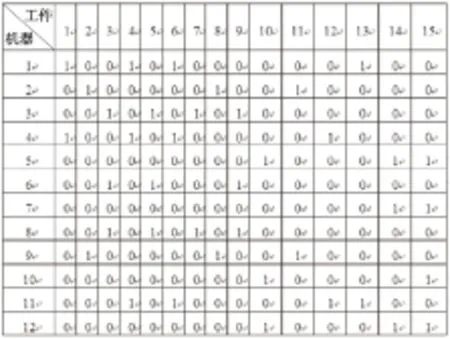
最后，为了保证获得的解是可行的，还须判断b[k]是否满足b[k]≥p: 如果满足，则该解是可行的。如果不满足，则撤消加工中心k，并对该中心的机器重新进行分配：从xi可获得所有分配在该中心的机器，如机器j。那么，需从概率矩阵Pi的第j行中找出满足p<所分配的机器数目

秀珠是个性急的人，忍耐不住，次日便到金家来了。一进门，就见一辆汽车停在门口，梅丽挟着一包书，从车上下来。秀珠便叫道：“老八刚下学吗？”梅丽回头一看，笑道：“好几天不见哩，今天你来好极了，我约了几个人打小扑克你也加入一个。”秀珠笑道：“你们一家人闹罢，肥水不落外人田，别让我赢去了。”梅丽对秀珠望着，将左眼目夹了一下，笑道：“你不是我一家人吗？就让你赢了去了，也不是肥水落了外人田啦。”秀珠笑道：“你这小东西，现在也学会了一张嘴。我先去见你三嫂，回头再和你算帐。”梅丽笑道：“我不怕。我到六姐那里去补习法文，你到那里去找我得了。”谈毕，梅丽的皮鞋，得得地响着，已跑远了。

如此，可确保最终获得一个可行解。

3.6 算法描述

步骤1输入矩阵A，计算相关参数。初始化种群，并计算种群的适应度值，具有最大适应度值的个体作为Elite。

步骤2如果当前迭代次数t大于最大迭代次数gen，算法终止，输出最优解。

步骤3N个个体进行搜索：

步骤3.1根据式(5)更新信息素值；

步骤3.3根据式(12)计算概率值；

步骤3.4将概率矩阵映射为问题的可行解；

步骤3.5计算N个个体的适应度，选取本次迭代产生的最优个体，如果该最优个体的适应度大于Elite的适应度，则选该个体为Elite；

步骤3.6根据式(9)和式(10)更新记忆矩阵，转步骤2。

4 仿真实验

4.1 参数选择

参数选择是群智能算法的一个难题，目前基本都通过实验分析手段确定其取值。本文所提出的NACA主要引入了三个参数：增强学习因子Q、听觉清晰度因子c、听觉中枢灵敏度lmd，三者主要影响听觉信号产生和处理函数的斜率和上限。本文采用不同参数组合的函数图像来确定它们的取值，过程如图1所示。经过分析比对得出，取c=2.0，Q=25，lmd=0.3，能较好地适应大多数情况。

Figure 1 Function curves for determining the values of Q,c,and lmd

根据以往研究及实验结果[4～11]，将其它参数设置为：种群总数N=40，总迭代次数gen=1 000，当前进化代数t=0，ρ=0.4，γ=0.6，αstart=3，βstart=1.5，αend=1.5，βend=3.0。

4.2 实例测试

提出的算法被应用于解决文献[15]所示的基准问题。另外，本文采用的测试算法均采用VisualC++ 6.0编程实现，且在同一台计算机上各运行50次，取最优解。若当前迭代次数t大于总迭代次数gen，则算法终止。

(1)简单实例。

该实例包含了12个机器和15个工件。机器和工件的初始关系矩阵A如图2所示。

Figure 2 Original incidence matrix A of machines/parts

显然，机器台数m=12，工件种数n=15。令q=4，p=2，则3≤Ncell≤6。

采用NACA算法最终获得的最优解为(3,4,1,3,2,1,2,1,4,2,3,2)，其对应的目标函数值为3。由定义1可知，组成加工中心1的机器有：3,6,8；组成加工中心2的机器有：5,7,10,12；组成加工中心3的机器有：1,4,11；组成加工中心4的机器有：2,9。

蚁群算法、蚁群算法中加入听觉信号、蚁群算法中加入记忆矩阵及NACA的收敛性如图3所示。

Figure 3 Comparison of the convergence speed of the four algorithms

实例1的测试结果表明，NACA可对一个具体问题进行求解，并找到最优组成方案，说明算法是可行的。

图3表明，在蚁群算法中分别引入听觉信号或记忆矩阵，算法的收敛性要优于蚁群算法，由此说明在蚁群算法中加入听觉信号或记忆矩阵，可加快算法的收敛速度；在蚁群算法中同时加入听觉信号和记忆矩阵，即NACA算法，算法的收敛性要优于以上三种算法，从而证明NACA算法具有较快的收敛速度。

(2)其它实例。

文献[15]提出采用组功效来衡量求解加工中心组成问题算法的有效性。因此，针对文献[15]中的基准问题，采用各算法策略求得的组功效如表1所示。其中，混合遗传算法的数据来源于文献[15]。迭代次数1为前四种算法策略获得最大组功效所需的最少迭代次数。迭代次数2为本文NACA算法获得最大组功效所需的最少迭代次数。

表1表明，针对加工中心基准问题，在蚁群算法中分别引入听觉信号或记忆矩阵，求得的组功效要优于蚁群算法，由此说明在蚁群算法中加入听觉信号或记忆矩阵，对加工中心组成问题的求解是有效的；在蚁群算法中同时加入听觉信号或记忆矩阵，即NACA算法，只需较少的迭代次数就可求得较大的组功效，从而证明NACA算法具有较好的全局寻优能力，算法的性能较优。

5 结束语

本文针对蚁群算法在求解加工中心组成问题时，容易出现收敛速度慢及陷入局部最优的缺点，提出了一种新颖的蚁群算法，即引入了听觉信号和记忆矩阵。听觉信号的引入可发挥出精英个体Elite对整个种群进化的推动作用，记忆矩阵的引

Table 1 Comparison of group efficiency obtained by different algorithms表1 不同算法策略求得的组功效比较

入可促使蚂蚁不断积累经验，更好地进行搜索。实验阶段，通过函数图像比对确定了重要参数的取值；通过对简单实例进行求解，验证了NACA算法是可行的，收敛性比对结果说明NACA算法的收敛速度较快；通过对基准问题进行求解，结果表明NACA算法获得较大组功效所需的迭代次数较少。这一切表明，NACA算法是可行的，收敛速度快，性能较优。

[1] Wang Ding-wei,Wang Jun-wei,Wang Hong-feng. Intelligent optimization methods[M]. Beijing: High Education Press,2008.(in Chinese)

[2] Mou De-yi,Liu Jin-feng. An improved ant colony algorithm for aircraft routing[J].Computer Engineering & Science,2012,34(6):136-139.(in Chinese)

[3] Zhang Jian-min,Qiahan·Hezier,Gao Da-li. A study of the logistic distribution routing problem based on the improved ant colony algorithm[J]. Computer Engineering & Science,2010,32(7):117-119.(in Chinese)

[4] Islier A. Group technology by an ant system algorithm[J]. International Journal of Production Research,2005,43 (5): 913-932.

[5] Muruganandam A, Prabhaharan G, Asokan P, et al.A memetic algorithm approach to the cell formation problem[J]. International Journal of Advanced Manufacturing Technology,2005,25(9-10):988-997.

[6] Mak K L,Peng P,Wang X X,et al. An ant colony optimization algorithm for scheduling virtual cellular manufacturing systems[J]. International Journal of Computer Integrated Manufacturing,2007,20 (6):524-537.

[7] Kao Y,Li Y L. Ant colony recognition systems for part clustering problems[J]. International Journal of Production Research,2008,46 (15):4237-4258.

[8] Megala N,Rajendran C,Gopalan R. An ant colony algorithm for cell-formation in cellular manufacturing systems[J]. European Journal of Industrial Engineering,2008,2 (3):298-335.

[9] Spiliopoulos K,Sofianopoulou S. An efficient ant colony optimization system for the manufacturing cells formation problem[J]. International Journal of Advanced Manufacturing Technology,2008,36(5-6):589-597.

[10] Li X,Baki M F,Aneja Y P. An ant colony optimization me-

ta-heuristic for machine-part cell formation problems[J]. Computers & Operations Research,2010,37:2071-2081.

[11] Xing B, Gao W J, Nelwamondo F V, et al. Part-machine clustering: The comparison between adaptive resonance theory neural network and ant colony system[J]. Lecture Notes in Electrical Engineering,Advances in Neural Network Research and Applications,2010,67 (8): 747-755.

[12] Shang Yu-chang. The visual,auditory and tactile communication of the ants[J]. Bulletin of Biology,2006,41(7):21-22.(in Chinese)

[13] Zhang Jun-hui,Gu Xian-hong,Hao Yue. Voice connections and interactions between sows and piglets[J]. China Animal Husbandry & Veterinary Medicine,2011,38(8):113-117.(in Chinese)

[14] Wu Yue-song.A study of underwater target recognition based on auditory model[M].Xi’an:Northwestern Polytechnical University,2005.(in Chinese)

[15] Goncalves J F,Resende M G C. A hybrid genetic algorithm for manufacturing cell formation:TD-5FE6RN[R]. AT&T Labs Research Technical Report,2002.

附中文参考文献：

[1] 汪定伟,王俊伟,王洪峰.智能优化方法[M].北京:高等教育出版社,2008.

[2] 牟德一,刘金凤.改进的蚁群算法在飞行路径模型中的应用[J].计算机工程与科学,2012,34(6): 136-139.

[3] 张建民,恰汗·合孜尔,高大利.基于改进蚁群算法的物流配送路径问题研究[J]. 计算机工程与科学,2010,32(7):117-119.

[12] 尚玉昌. 蚂蚁的视觉、听觉和触觉通讯[J]. 生物学通报,2006,41(7):21-22.

[13] 张俊辉,顾宪红,郝月.母猪与仔猪的声音联系及互作[J].中国畜牧兽医,2011,38(8):113-117.

[14] 吴岳松.基于听觉模型的水下目标识别研究[M].西安：西北工业大学,2005.

吕聪颖(1981-),女,河南襄城人，硕士，讲师，研究方向为智能算法。E-mail:Lvcongying0601@126.com

LÜ Cong-ying,born in 1981,MS,lecturer,her research interest includes intelligent algorithm.

A study of the cell formation problems based on a novel ant colony algorithm

LÜ Cong-ying

(School of Computer and Information Engineering,Nanyang Institute of Technology,Nanyang 473000,China)

The ant colony algorithm for solving cell formation problems tends to fall into early mature convergence status. In order to overcome this defect, we propose a mixed algorithm of the ant colony algorithm, the auditory signal and the memory matrix. In the simulation experiments, the ant colony algorithm, the ant colony algorithm containing auditory signals, the ant colony algorithm containing memory matrixes, and the proposed novel algorithm are adopted respectively to solve cell formation problems. Experimental results show that the proposed algorithm outperforms the other three in terms of enhancing global optimization capacity and convergence speed of the ant colony algorithm. At the same time, the group efficiency obtained by the proposed algorithm is better than the three aforementioned algorithms and the existing hybrid genetic algorithms.

the novel ant colony algorithm;pheromone;auditory signal;memory matrix

1007-130X(2015)09-1712-06

2014-03-05;

2014-09-13基金项目：国家自然科学基金青年基金资助项目(81101490);国家自然科学基金资助项目(61175023)

TP301.6

A

10.3969/j.issn.1007-130X.2015.09.019

通信地址：473000 河南省南阳市长江路80号南阳理工学院计算机与信息工程学院办公室

Address:School of Computer and Information Engineering,Nanyang Institute of Technology,80 Changjiang Rd,Nanyang 473000,Henan,P.R.China