一种基于JADE改进的差分演化算法*
2015-01-05李康顺王法杰张楚湖
李康顺,王法杰,张楚湖,杨 磊,陈 琰
(华南农业大学信息学院,广东 广州 510642)
一种基于JADE改进的差分演化算法*
李康顺,王法杰,张楚湖,杨 磊,陈 琰
(华南农业大学信息学院,广东 广州 510642)
差分演化算法有局部搜索能力不足、容易跌入局部最优等缺点,其搜索性能主要依赖于对杂交概率和缩放因子的设置。为了改善上述缺陷,对带归档的自适应差分演化算法JADE进行深入的研究与分析,提出了改进的自适应差分演化算法ZJADE。该算法采用斜帐篷混沌映射函数初始化种群,在每次迭代中为每个个体分别产生满足正态分布、柯西分布的杂交概率和满足正态分布的缩放因子,并且记录成功变异个体的杂交概率和缩放因子,引入统计杂交概率,采用两种策略自适应地更新杂交概率。在13个经典测试函数上将ZJADE算法与多种经典自适应差分演化算法进行对比,实验结果表明,ZJADE算法在解的精度与收敛速度上更优,具有更好的搜索性能。
自适应差分演化算法;混沌映射;统计杂交概率;柯西分布;正态分布
1 引言
差分演化算法已经被证明是现实世界优化问题的一种简单有效的演化算法[1]。国内外对差分演化算法的理论研究主要集中于算法的收敛性分析、计算复杂度的分析和空间复杂度的分析。Zaharie D[2]给出了差分演化收敛性的理论分析,并指出了缩放因子、杂交概率和种群大小间的数值关系。Dasgupta S等人[3]采用动力学的特性对基本差分演化算法寻优过程进行理论方面的探讨分析,结果表明差分演化算法采用类似梯度下降的搜索策略以快速向全局最优解逼近,其中杂交概率能够决定算法的收敛性。差分演化算法的性能主要依赖于三个控制参数,即杂交概率CR、缩放因子F和种群规模NP。它在局部搜索能力表现不足,在处理高维度问题上收敛速度慢,求解精度不高的问题较为突出。尽管针对控制参数设置方面的研究有一些成果,但是其参数设置和优化性能之间的相互作用是复杂的,并且不能被完全表示出来。究其主要原因是没有固定的参数能适用于各类优化问题,甚至在一个单一问题的不同优化阶段中参数的设置对算法的优化性能有着很大的影响。国内外针对差分演化算法的以上不足做出的相应研究有,Qin A K等人[4]首次提出了采用两种变异策略的自适应的差分演化算法SaDE(Self-adaptive Differential Evolution),之后Qin A K等人[5]又对该自适应算法进行了改进,改进后该算法不仅可以自适应调整缩放因子和杂交概率,而且算法在四种不同的策略中自动选择,不同的策略适应不同的演化阶段,极大地提高了算法的收敛性。Brest J[6]提出了自适应差分演化算法jDE,在jDE中,缩放因子F和杂交概率CR与种群个体一同编码和迭代。通过两个参数τ1 和τ2随机动态地产生新的F和CR。Zhang等人[1]提出了一种新的自适应差分演化算法JADE,JADE在迭代过程中记录成功参与差分变异的个体缩放因子和杂交概率,为每个个体分别产生服从正态分布和柯西分布的缩放因子和杂交概率,该算法包括带归档种群和不带归档种群两种。JADE算法在优化性能上、收敛速度、求解精度等各个方面都优于现有的一些改进的差分演化算法。
本文深入探讨JADE的实现机理,并对JADE算法加以改进,应用混沌映射函数进行种群的初始化,提出基于统计结果和采用不同分布的自适应策略改变杂交概率和缩放因子的自适应差分演化算法,实现在求解精度和收敛速度上提高算法的搜索性能,并采用CEC2005的13个基准函数进行测试,以检验算法的有效性。
2 差分演化算法
2.1 差分演化算法的基本步骤
2.1.1 编码及其初始化
设求解问题的维度为D,种群规模为NP,问题的上下界分别为Up和Low。第G代的个体种群为:
XG=(x1,G,x2,G,…,xNP,G)
(1)
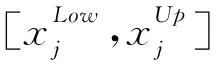
(2)
2.1.2 差分变异
差分变异操作一般采用形如“DE/x/y/z”加以区分。其中x表示基向量是采用rand(随机选择的)还是best(当前最好的),y表示所用差分向量的个数,z表示交叉的方式,一般分为二项式交叉(bin)和指数交叉(exp)两种方式[7]。例如,等式(3)为“DE/rand/1/bin”变异策略,随机从种群中挑选出一个个体向量作为基向量(也称扰动向量)和两个不同的个体作为差分向量,通过式(3)可得到变异向量。
(3)

下面是另外几种常见的模式。
(1)DE/rand/2/bin
(4)
(2)DE/best/1/bin
(5)
(3)DE/best/2/bin
(6)
(4)DE/current-to-best/1/bin
(7)
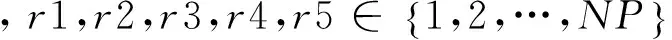
2.1.3 交叉操作
将变异向量vi,G+1和原向量xi,G按照式(8)进行交叉操作,得到实验向量。
(8)
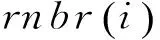
2.1.4 选择操作
DE采用一对一的选择操作方式,将交叉操作得到的实验向量ui,G+1和原向量xi,G按式(9)进行择优选择,适应值较优的个体向量进入下一代。
(9)
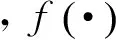
2.2 自适应差分演化算法JADE
JADE在迭代过程中为每个个体i都产生服从正态分布的CRi和柯西分布的Fi,在迭代过程中记录成功参与差分变异的个体的CRi和Fi,最后取其均值,按照指定公式产生新的CRi和Fi进行演化。该算法有带归档种群和不带归档种群两种,下面以带归档种群为例介绍其算法流程:
(1)初始化交叉概率因子μCR和缩放因子μF,归档种群A为空集。随机产生种群规模为NP的向量个体种群P,最大迭代次数Gmax,设置迭代器G=0,成功参与变异的个体的交叉概率因子SCR和缩放因子集合SF分别为空集。
(2)对于第G代的每个个体i,按照式(10)和式(11)分别产生服从正态分布的CRi和柯西分布的Fi。当CRi和Fi的值小于0时截断为0,当CRi和Fi的值大于1时截断为1。
CRi=randni(μCR,0.1)
(10)
Fi=randci(μF,0.1)
(11)
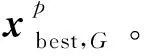
(12)
(13)
(14)
(4)遍历第G代的所有个体后,如果集合A的种群规模大于NP,随机移除个体使其规模不大于NP,然后根据如式(15)和式(16)更新μCR和μF。
(15)
(16)
其中,c为控制因子,范围为(0,1),meanA(SCR)表示对集合SCR求出的均值,meanL(SF)表示对集合SF按照式(17)求出的Lehmer平均值。
(17)
(5)迭代器G加1,判断是否满足终止条件,如果不满足,跳转到步骤(2),否则算法结束。
不带归档种群的JADE与带归档种群的JADE之间的区别在于后者进行差分演化的个体是从当前种群随机获取,即xr2,G≠xr1,G≠xi,G∈P。
3 改进的JADE
3.1 混沌映射函数
混沌运动具有其独特的性质:随机性,类似随机变量的杂乱表现;遍历性,不重复历经一定范围内的所有状态;规律性,由确定性的迭代式产生[8]。混沌映射函数的遍历性是差分演化算法初始化种群迭代函数的出发点。混沌映射函数有很多,其中两个简单的比较有名的映射为:
(1)Logistic映射。
xn+1=μxn(1-xn)
(18)
当3.569946<μxn(1-xn)<4,x∈(0,1)时系统处于混沌状态。
(2)Skew tent map斜帐篷映射。
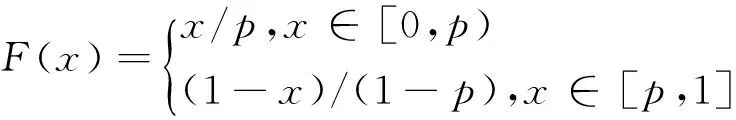
(19)
当控制参数p∈(0,1)时系统处于混沌状态。
从参数范围可以看出,斜帐篷映射的取值范围更大,斜帐篷映射的变量密度比Logistic映射要稳定。Logistic映射所产生的混沌变量分布不均匀,而斜帐篷映射则相对均匀,更满足均匀分散、齐整可比的分布要求。故在本文的混沌映射函数中采用斜帐篷映射初始化种群,既不改变差分演化算法初始化时所具有的随机性,同时利用了混沌特性提高种群多样性和种群个体搜索的遍历性。
3.2 改进的自适应差分演化算法ZJADE

假设当前迭代过程中成功变异总个体为NP′,由此得出统计杂交概率statmean。具体如下:
(20)
(21)
(22)
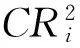
3.3 ZJADE算法流程
改进后的自适应差分演化算法ZJADE的伪代码如下:
Begin
Set μCR=0.5;μF=0.5;A=∅; and initial population{xi,0|i=1,2,…,NP}
Forg=1 toG
SF=∅;SCR=∅;NP′=0
Fori=1 to NP
CRi=randni(μCR,0.1);
CR2i=randci(μCR,0.1);
Fi=randni(μF,0.1);
jrand=randint(1,D);
For j=1toD
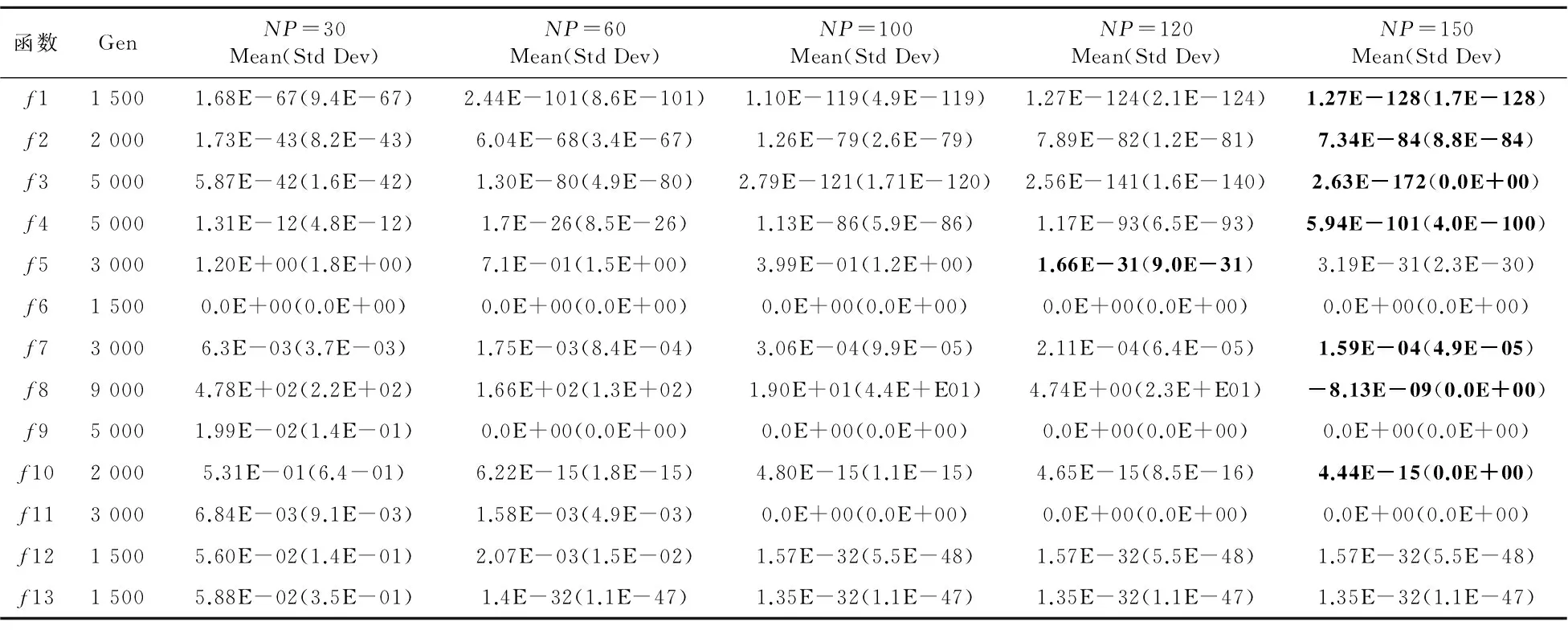
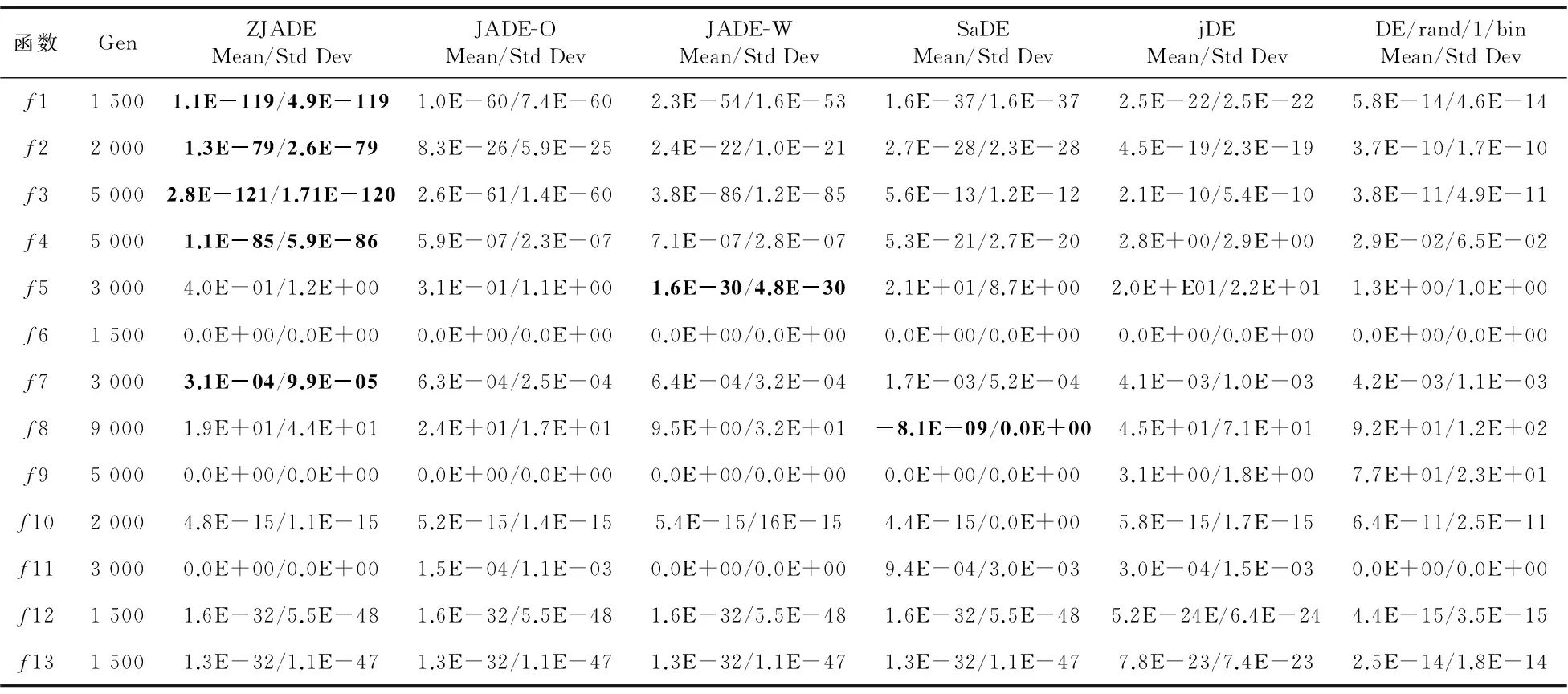
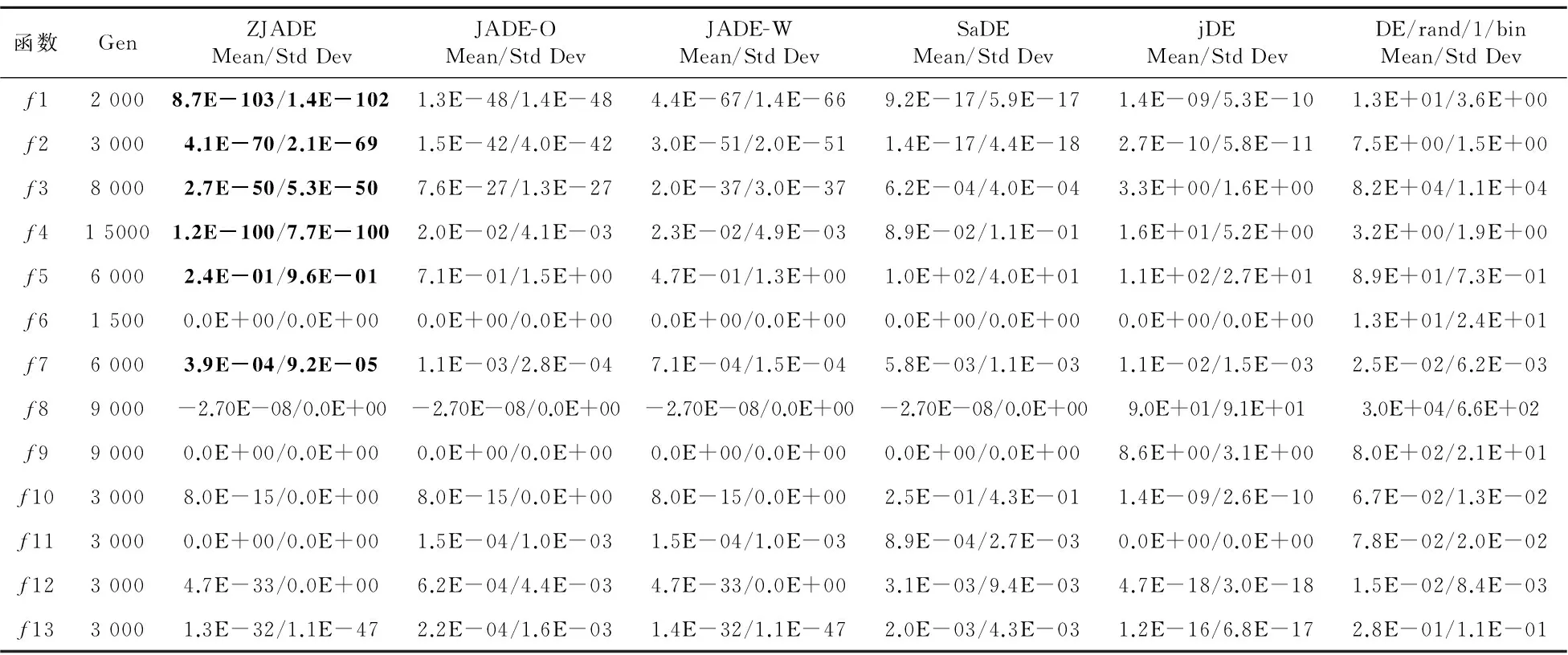
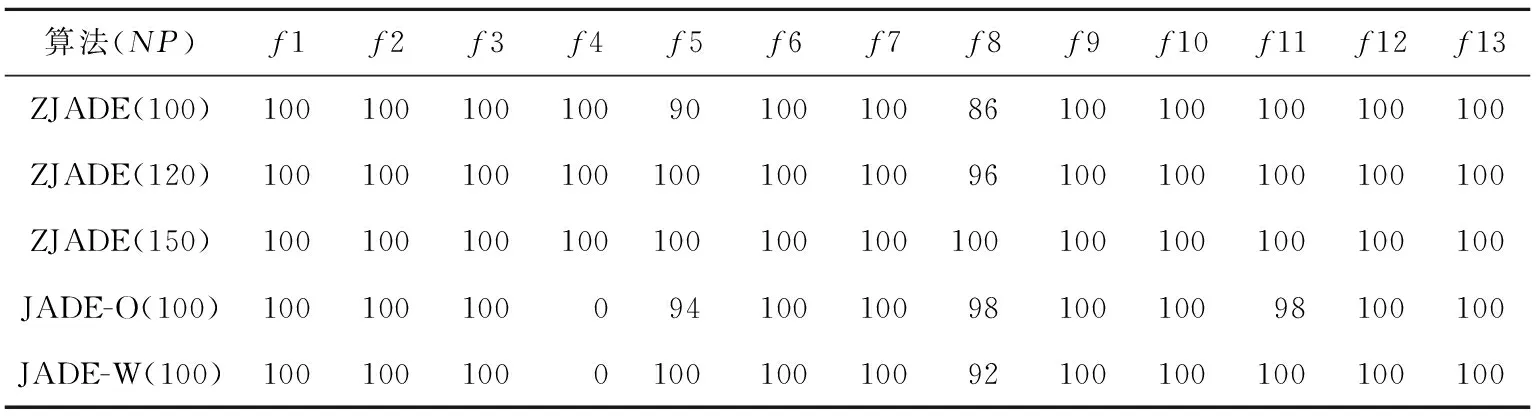
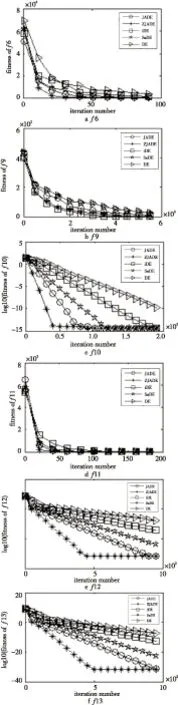
If(rand(0,1) uij,g=vij,g; Elseuij,g=xij,g; EndIf EndFor Forj=1toD EndIf EndFor If(f(u2i,g)≤f(ui,g)) End If If (f(xi,g)≤f(ui,g)) Else xi,g+1=ui,g xi,g→A; CRi→SCR; Fi→SF; NP′=NP′+1; Forj=1 toD diffij=0; Elsediffij=1; EndIf EndFor EndIf EndFor If(statmean End If End For End 相对于JADE算法而言,新的自适应算法在总的算法复杂度上没有增加。算法增加额外复杂度是对比两种概率下得到的两个实验个体向量以及计算统计杂交概率,该算法复杂度为O(G*NP+G*NP*D)。由于JADE算法总的复杂度O(G*NP*(D+log(NP))),其中G为最大的迭代次数,所以新的自适应差分演化算法的复杂度也是O(G*NP*(D+log(NP)))。一般来说种群规模大小NP的设置与问题的维数D相关。 为了验证所提出的改进的自适应差分演化算法(ZJADE)的性能,本文选取Benchmark函数进行仿真实验分析与比较。表1列出了Benchmark函数,以及函数的取值范围和最优解。其中Benchmark函数(f1~f13)用于30维和100维实验,这些函数是CEC2005上的13个标准函数优化测试问题,这些问题一直被广泛地应用于演化优化领域算法性能的测试。问题f1~f4是连续单峰问题;问题f5是Rosenbrock函数,当维度为2或者3时,函数是单模的,但高维情况下有多个局小值;问题f6是一个非连续的阶梯型函数;f7是一个带有噪声的多项式问题;f8~f13是多峰的,并且问题所包含的局部极小值随着问题维数的增大而呈指数倍增长。 4.1 问题的具体定义 相关函数的具体定义可以参考文献[1]。 4.2 Benchmark问题实验与分析 为了验证本算法的有效性,和JADE以及其他自适应动态差分演化算法jDE、SaDE,以及基本差分演化算法DE(DE/rand/1/bin)进行对比实验,并加以分析。其中jDE(τ1=τ2=0.1,Fl=0.1,Fu=0.9)和SaDE(LP=50)采用原始论文的实验参数设置,基本差分演化算法的参数设置为:F=0.5,CR=0.9。对于本文提出的ZJADE参照JADE的参数设置:μCR=0.5,μF=0.5,c=0.1,p=0.05。 Table 1 Description of the test functions表1 测试函数的说明 从表2可以得出算法收敛的精度受种群规模大小的影响比较大。当种群大小设置为NP=30时算法的收敛效果最差,NP=150时算法的收敛效果最好。随着种群规模的增加,规模从2*D到5*D,收敛精度的提升总体已经不是很明显,其提升主要是在简单的单模函数上。 对于所有算法,当问题D=30或100维时,对应的种群规模分别设置为NP=100或400。求解精度VTR(Value-To-Reach)对于f7设定VTR=10-2,其他的函数设定VTR=10-8。所有函数都独立运行50次,得到的平均误差和均方差如表3和表4所示。在所有算法中每个函数寻优能力最好的结果用粗体表示出来。表5和表6表示不同算法运行的成功率SR。 从表3和表4可以看出,改进的算法无论是在30维实验还是在100维的数据实验上大多数函数的收敛结果都比原来的JADE好。在30维的实验上,相对JADE,ZJADE在简单的多峰值问题f1~f4上收敛精度提升很多。从表5和表6上可以看出,改进的算法基本上维持原来JADE较好的稳定性。该算法在30-D上算法的稳定性相比JADE在函数f5和f8上相对较差,但是在表2中ZJADE 针对不同种群规模在30-D函数的实验结果比较中可以看出,相对于30-D而言,种群设置为100并不是最好的选择,当种群规模提升到120时候,ZJADE的在f5和f8函数上的成功率SR分别提升到了100%和96%;而当种群规模提升到了150的时候, Table 2 Experimental results of 30-Dimensional problems f1~f13 according to ZJADE ofdifferent population sizes averaged over 50 independent runs表2 ZJADE针对不同种群规模在30-D函数的实验结果 Table 3 Experimental results of 30-Dimensional problems f1~f13 according to ZJADE compared with other DEs表3 ZJADE与其他DE的30-D函数实验结果比较 Table 4 Experimental results of 100-Dimensional problems f1~f13 according to ZJADE compared with other DEs ofdifferent population sizes averaged over 50 independent runs表4 ZJADE与其他DE的100-D函数实验结果比较 Table 5 Experimental success rate comparison between ZJADE’s function and JADE’s in 30-Dimension表5 ZJADE与JADE的30-D函数实验成功率比较 Table 6 Experimental success rate comparison between ZJADE’s function and JADE’s in 100-Dimension表6 ZJADE与JADE的100-D函数实验成功率比较 Figure 1 Trend of fitness of the five algorithms about problems f1~f4 ZJADE在f5和f8函数上的成功率SR都达到了100%。随着问题维数的增加,改进算法的搜索性能优势进一步体现出来,无论是收敛精度还是收敛的稳定性方面都是所有算法中最好的。在100-D的实验测试上,ZJADE在所有基准函数上都达到了最优,除了函数f5外其他函数在50次独立运行中都能够100%达到预定的VTR,远好于原来的JADE。 为了显示清楚,在图1和图2中有些函数并没有显示出所有的迭代次数变化图,对于纵坐标有些函数则采用了对数方式。从MATLAB实验仿真图可得出,通过改进种群初始化策略和杂交变异策略使得改进的自适应差分演化算法ZJADE在收敛速度上优于其他四种算法。从图1中看到,在连续单模函数(f1~f3)上ZJADE适应值变化比较陡峭,而且最终的适应值要比其他几种算法好得多。 相对于其他算法,该算法在f4和图2中的函数上一开始的适应值的变化比较陡峭,最后比较平稳的收敛到最优解。ZJADE算法在收敛速度、求解精度上都优于其他四种算法,同时也表现出较好的稳定性。 Figure 2 Trend of the fitness of the five algorithms about problems f6 and f9~f13 本文提出的ZJADE算法相比JADE算法主要改进是利用斜帐篷映射函数对差分演化算法进行种群初始化,使得生成的种群满足均匀分散、齐整可比的分布特点;基于统计结果,当成功变异的个体在种群中的比例超过预设的阈值时,更新杂交算子采用实验向量ui,G+1与原向量xi,G之间的Hamming距离与问题的维数之间的比值,否则采用成功变异个体杂交概率的均值;在产生每个个体的杂交概率和缩放因子时,杂交概率同时采用正态分布和柯西分布,缩放因子采用正态分布。分别在问题维度为30维和100维的实验数据上对13个基准函数进行仿真实验。结果表明,ZJADE能改进算法的全局搜索能力,提高差分演化算法的搜索性能,在求解精度和收敛速度上优于其他的四种算法,并且这种效果在100维的仿真实验上体现得更加明显。后续工作将ZJADE运用到实际问题和更复杂的问题中,此外自适应算子也是研究的重点。 [1] Zhang J,Sanderson A C. Jade: Adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation,2009,13(5):945-958. [2] Zaharie D. Critical values for the control parameters of differential evolution algorithms[C]∥Proc of MENDEL the 8th International Conference on Soft Computer,2002:62-67. [3] Dasgupta S,Das S,Biswas A,et al.On stability and convergence of the population-dynamics in differential evolution[J]. Ai Communications,2009,22(1):1-20. [4] Qin A K,Suganthan P N. Self-adaptive differential evolution algorithm for numerical optimization[C]∥Proc of IEEE Congress on Evolutionary Computation,2005:1785-1791. [5] Qin A K,Huang V L,Suganthan P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation,2009,13(2):398-417. [6] Brest J,Greiner S,Boskovic B,et al. Self-adapting control parameters in differential evolution:A comparative study on numerical benchmark problems[J]. IEEE Transactions on Evolutionary Computation,2006,10(6):646-657. [7] Price K,Storn R M,Lampinen J A. Differential evolution:A practical approach to global optimization[M]. Berlin and Heidelberg:GmbH,2006. [8] Guo Zhen-yu,Cheng Bo,Ye Min, et al. Parallel chaos differential evolution algorithm[J].Journal of Xi’an Jiaotong University,2007,41(3):299-302.(in Chinese) [9] Gong W,Cai Z,Wang Y. Repairing the crossover rate in adaptive differential evolution[J]. Applied Soft Computing,2014,15:149-168. 附中文参考文献: [8] 郭振宇,程博,叶敏,等. 一种并行混沌差异演化算法[J]. 西安交通大学学报,2007,41(3):299-302. 李康顺(1962-),男,江西兴国人,博士,教授,CCF会员(E200007519S),研究方向为智能计算、图像识别、数据挖掘、嵌入式系统、演化硬件和神经网络。E-mail:likangshun@sina.com LI Kang-shun,born in 1983,PhD,professor,CCF mem- ber(E200007519S),his research interests include intelligent computation, image identification, data mining, embedded system, evolvable hardware, and neural network. 王法杰(1990-),男,四川巴中人,硕士生,研究方向为演化计算和嵌入式系统。E-mail:836563248@qq.com WANG Fa-jie,born in 1990,MS candidate,his research interests include evolutionary computation, and embedded system. 张楚湖(1988-),男,广东普宁人,硕士,研究方向为演化计算。E-mail:813777109@qq.com ZHANG Chu-hu,born in 1988,MS,his research interest includes evolutionary computation. 杨磊(1978-),男,河南方城人,博士生,讲师,研究方向为计算机体系结构、微处理器设计和人工智能。E-mail:Yanglei_s@scau.edu.cn YANG Lei,born in 1978,PhD candidate,lecturer,his research interests include computer architecture, microprocessor design, and artificial intelligence. 陈琰(1977-),女,宁夏吴忠人,博士生,讲师,研究方向为图像处理和演化计算。E-mail:cheny@scau.edu.cn CHEN Yan,born in 1977,PhD candidate,lecturer,her research interests include image processing, and evolutionary computation. An improved differential evolution algorithm based on JADE LI Kang-shun,WANG Fa-jie,ZHANG Chu-hu,YANG Lei,CHEN Yan (College of Information,South China Agricultural University,Guangzhou 510642,China) Differential evolution algorithms are weak in local searching and easy to dropping into the local optimal solutions at the same time. The search performance of these algorithms is mainly based on the parameter setting of their crossover probability and mutation factors. To improve the above shortcomings of differential evolution algorithms, we propose an adaptive differential evolution algorithm called ZJADE on the basis of in-depth research and analysis of the adaptive differential evolution with optional external archive (JADE). Skew tent chaotic mapping is used to initialize the population in order to generate uniformly dispersed population. During each generation, the crossover probability of each individual is generated according to the normal distribution and the Cauchy distribution while the mutation factors are independently generated according to the normal distribution. The crossover probability and mutation factors of successful individuals are saved, and the statistical crossover probability is employed. The ZJADE algorithm is compared with multiple state-of-the-art adaptive differential evolution algorithms through thirteen classical test functions. The results show that the ZJADE obtains better solution accuracy and quicker convergence speed, thus having a better search performance. adaptive differential evolution algorithm;chaotic mapping;statistical crossover probability;Cauchy distribution;normal distribution 1007-130X(2015)09-1698-09 2014-11-18; 2015-01-27基金项目:广东省自然科学资金资助项目(2014A030313454);国家星火计划资助项目(2013GA780033) TP301.6 A 10.3969/j.issn.1007-130X.2015.09.017 通信地址:510642 广东省广州市华南农业大学信息学院 Address:College of Information,South China Agricultural University,Guangzhou 510642,Guangdong,P.R.China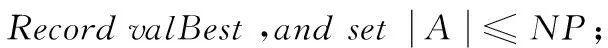
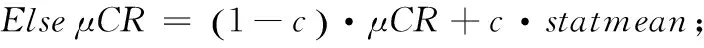
4 实验结果及分析



5 结束语






