基于OpenCL的Lammps短程力算法优化研究*

赵成龙 ，施慧彬 ，俞忻峰

(1.南京航空航天大学计算机科学与技术学院,江苏 南京 210016;2.南京理工大学计算机科学与技术学院,江苏 南京 210094)

基于OpenCL的Lammps短程力算法优化研究*

赵成龙1，施慧彬1，俞忻峰2

(1.南京航空航天大学计算机科学与技术学院,江苏 南京 210016;2.南京理工大学计算机科学与技术学院,江苏 南京 210094)

Lammps是用于分子动力学模拟及其相关问题的一款开源软件，可利用其了解固体、液体性质，应用广泛。支持使用CUDA及OpenCL进行GPU加速。因OpenCL具有跨平台特性，将其作为研究重点。总结了OpenCL内核编程中需要注意的设计原则并阐述了一种改进的阿姆达尔定律用于衡量异构平台理论加速性能。测试了Lammps短程力计算在Y485P平台下的性能参数。通过对短程力计算中的关键部分如邻接表的建立及短程力计算部分的内核代码进行优化，使其取得了更好的加速效果。

GPU;Lammps;OpenCL;分子动力学;短程力;内核优化

1 引言

分子动力学模拟的基本原理为建立一个合适的粒子系统，利用牛顿运动方程确定系统中各个粒子的运动情况，通过求取粒子动力学方程组的数值解，决定系统中的各个粒子在相空间中的运动规律，最终通过统计物理及热力学原理得出系统相应的宏观物理特性。其初始研究可以追溯到1957年Alder B J和Wainwright T E的硬球模型[1]。随着其发展，应用领域逐渐涵盖化学、物理、能源、生物、材料、医学等多个领域，因其运算量庞大、耗时长的特点，一直制约了其发展。

大规模原子分子并行模拟器Lammps(Large-scale Atomic/Molecular Massively Parallel Simulator)主要用在分子动力学相关的一些计算和模拟上，是美国Sandia国家实验室开发并以GPL licence发布的开放源代码的分子动力学软件。Lammps可以支持气态、液态或者固态的各种系统下，千万级以及上亿级规模的原子分子体系，并支持多种势函数，具有良好的并行扩展性[2]。

除Lammps之外,还有流行的分子动力学模拟软件如NAMD[3]、Amber[4]、Gromacs[5]也采用了GPU进行加速。OpenCL因其可跨平台使用的特点越来越多地被分子动力学软件采用。 Lammps中基于OpenCL的GPU加速包由Brown W M等在文献[6～8]中提出。同时，基于OpenCL的分子动力学模拟加速还有文献[9]提出的一种性能自适应的分子动力学模拟内核。对于OpenCL内核优化工作，目前大多数的研究主要针对内存的读取、资源利用率及算法本身等的优化，而对内核代码的优化，目前没有出现过详细阐述，如文献[10]阐述了访存效率、资源利用率、硬件资源限制对性能的影响及优化方式。文献[11,12]仅对内核编程中需要注意的极少部分进行了阐述。

本文详细总结了OpenCL内核编程过程中的原则。阐述了一种改进的阿姆达尔定律，可用于异构平台下的性能评估。通过研究Lammps中的短程力LJ(Lennard-Jhones)力实现部分，对邻接表建立、力的计算部分分别进行优化，对比优化前后的性能,验证了内核程序的优化有助于算法性能的提升。

2 OpenCL内核优化编程

2.1 OpenCL简介及平台信息

开放计算语言OpenCL[13](Open Computing Language)是第一个面向异构系统的通用并行编程标准，其特点是免费、跨平台以及良好的互操作特性。它为软件开发人员提供了统一的编程环境，广泛适用于多核处理器(CPU)、图形处理器(GPU)、Cell类型架构等并行处理器，拥有广阔的发展前景。其标准可利用平台模型、执行模型、内存模型、编程模型进行描述。

本文所使用的测试平台为联想Y485P笔记本，CPU型号为A10-5750M，主频2.5 GHz。平台显卡信息如表1所示，其中HD8650G为集显。测试系统为Ubuntu 13.10。

2.2 并行加速理论模型

在并行编程中，衡量多核环境下并行应用在固定负载下并行处理效果的加速比S，通常使用阿姆达尔定律(Amdahl’s Law)。该定律描述了系统中

Table1 Test platform information表1 测试平台信息

并行以及串行所占系统计算比重对于加速比的影响,公式如下：

(1)

其中，s为系统中串行部分所占比例，p为整个应用中并行所占比例(为1-s)，N为处理器个数。

阿姆达尔定律对多核系统中负载恒定的理想情况下是成立的，而当N→∞时，取得最大值：

S=1/s

(2)

式(2)说明，理想情况下，即使串行部分的工作很小，系统的加速比也只能够限制在1/s。

阿姆达尔定律的首要条件是系统中的信息传输开销可以忽略。但是，在使用GPU作为加速器件的情况这种开销将变得不可忽视。从平台整体架构来说，使用GPU进行加速的应用可以作为非对称处理器的一种。文献[14]就这种情况下对阿姆达尔定律进行了改进，引入了两个新的参数：

(1)已并行加速比例p′:对于传统对称多核处理器，并行比例p最优化后的比例为p/N。然而，非对称多核处理器的加速内核相较串行内核在计算能力上有很大的不同，故使用p和N在公式中将变得没有任何意义。而真正在GPU上所实现的效果也会因为算法及其映射到加速内核上的方式的不同而有很大的区别。所以，应当将p转换成p′。

(2)并行损耗o:在传统对称多核处理器情况下，这种并行损耗通常是可以忽略的，因为通常内核间的通信代价很小。而对于加速器件平台(如GPU)来说，这部分的损耗就变得不可忽视，这主要是因为CPU内存与GPU内存之间的数据传输时间占程序执行时间的比重较大。

最终的加速比S′可以表示为：

(3)

从式(3)中可看出，若希望系统的加速比尽可能高，则必须找出系统中足够多的并行化部分代码，尽量减小s。同时，需要注意到的是，由于GPU的数据传输造成o比较大，将弱化并行化p′所获得的加速效果,这在后续的实验数据中也可以看出。这也为OpenCL的性能优化提供了一定的理论基础。

利用AMD公司提供的SDK中的BufferBandWidth例子，测得系统中两个GPU与CPU在不同数据大小(从2 KB～64 MB)情况下的传输速率。最终结果如图1所示。

Figure 1 Bandwidth test

图1a描述了从主机(CPU)到设备(GPU)的带宽。可以看到尽管HD8650G作为AMD推出的加速处理器APU(Accelerated Processing Unit)中的集显，排除了PCIE访问，但是仍然可以看出其数据传输相较HD8790M的独显来说，只有在超出一个阈值(Threshold)时这种优势才变得比较明显。图1b描述了相反方向的测试结果，即从设备(GPU)到主机(CPU)的测试结果。设备到主机的传输，该阈值比主机到设备要小。同时，设备到主机的最大带宽也略高于主机到设备的带宽。

这也从侧面印证了对于APU设备来说，在小数据量的情况下，数据的传输并没有克服PCIE带宽所带来的限制，但是从大数据量上来说，情况要好很多。这可能是由于数据在传输之前需要进行DMA传输的建立以及内存的固定(Pinning)操作有关。同时，对于本测试平台，HD8650G可以支持AMD的零拷贝特性(Zero Copy)但是直接的带宽量难以测得，使用Map(clEnqueueMapBuffer)内存的方式对写入和读取操作进行了进一步的测试，得到使用memset写零拷贝内存的带宽可达到4.179 GB/s，而读取操作则只有1.214 GB/s。

为了能够更好地发挥APU零拷贝特性，在使用APU进行异构加速运算时，对于内存的创建和读写建议通过以下方式进行：

(1)在创建内存对象时，除基本可访问特性外，通过增加CL_MEM_ALLOC_HOST_PTR、CL_MEM_USE_HOST_PTR或CL_MEM_USE_PERSISTENT_MEM_AMD进行内存创建。CL_MEM_ALLOC_HOST_PTR和CL_MEM_USE_HOST_PTR为OpenCL 1.2标准中所定义的内存分配方式，CL_MEM_USE_PERSISTENT_MEM_AMD为AMD平台扩展实现的内存分配方式。通过这些方式创建的内存具备零拷贝特性。

(2)在读取和写入时，不采用clEnqueueReadBuffer以及clEnqueueWriteBuffer的方式进行内存访问，使用clEnqueueMapBuffer以及clEnqueueUnmapMemObject的方式进行数据读写操作。注意，对于图像内存对象来说，只有使用CL_MEM_USE_PERSISTENT_MEM_AMD特性创建的内存对象才具备此特性。

通过上述方式，可以直接减少PCIE传输带来的内存传输开销，从而带来传输性能的提升。同时，查阅OpenCL 2.0标准还可发现，新的内存模型中集成的GPU和CPU将采用相同的内存地址范围，也就意味着真正零拷贝的实现。

2.3 内核优化原则

通过整理与测试，发现在OpenCL内核编程中，也有一些需要在编码过程中注意的地方，将其整理为如下内核编程原则：

原则1展开小规模循环：如果已知一个循环的边界值，并且该循环的规模是比较小的，比如指令为16～32个，可以展开该循环，这样避免了循环中的比较操作。展开的操作可以使用手工的方式或者使用编译命令#pragma unrollN展开循环。使用编译器命令时必须确定在编译时编译器可以获得循环的次数，否则不起作用。而使用手工方式则可以进行更加精细的控制，比如加入向量化运算特性、自主决定循环中同步操作的次数及位置。

原则2使用编译器命令传递常量：如果在内核中需要使用到一个常量，应当使用编译条件进行定义，而不是浪费一个内核参数进行传递。这样可以减少对本地内存或者私有内存的读取操作。例如，你想传入一个LEN的宏，可以通过如下方式：

clBuildProgram(program,0,NULL,”-DLEN=256”,NULL,NULL);

在编译这个内核时，程序将会把LEN的宏自动定义为256。

原则3在无需进行共享数据的情况下，使用私有内存(Private Memory)来代替本地内存(Local Memory)。工作项访问私有内存的速率比访问本地内存的速率要快，但是如果这些数据需要在工作组之间共享，则只能使用本地内存。需要注意的是，如果使用OpenCL操作的设备是CPU，则该原则不一定成立。例如，AMD中CPU设备的OpenCL实现，使用Cache进行模拟，则不一定会有优化效果。

原则4尽量避免使用%操作符：求余操作符在显卡上需要大量的处理时间，应当避免或者寻求其他的解决方式。

原则5内联化非内核函数：使用inline声明告诉编译器，在调用函数处对函数进行展开，可以免除上下文切换以及调用堆栈所造成的损失。

原则6使用内核函数：这里举一些例子进行说明：

(1)if-then-else语句会造成分支，使用select函数避免分支的产生，如：

if(x== 1)r=0.5;

if(x== 2)r=1.0;

可以改成：

r=select(r,0.5,x==1);

r=select(r,1.0,x==2);

(2)浮点运算的乘加运算，如果对速度要求大于精度要求，可使用mad以及fma函数进行乘加运算。

(3)带native_前缀的函数通常比不带native_前缀或带half_前缀的相应函数要性能更优，其精度由具体实现决定。

原则7使用分支预测而不是流程控制，如下面情况的代码：

if(A>B){

C+=D;

}else{

C-=D;

}

可改成：

intfactor=(A>B)?:1:-1;C+=factor*D;

这是因为前一个代码段会生成IF/ELSE/ENDIF的控制语句，每一个都将会花费～8的周期，整个代码可能花费到～36个周期。而下面部分的代码段只需要12个周期，可以提高至少1.3倍。

原则8通过顺序访问本地内存避免访问冲突：AMD的本地内存一般由32个库(Bank)组成，如果多个工作组访问同一个库，则访问操作将会串行化。而当同组中的相邻工作项访问相邻的库，可尽可能地减少串行化访问带来的损失。

原则9尽量采用float4、int4这样的向量数据类型，在内核参数中使用向量数据类型可以有效提高数据带宽。而在内核代码中使用该数据类型也更符合GPU架构并行化特点。同时，需要注意的是，对于AMD中的GCN(Graphics Core Next)架构的GPU来说，由于设备架构的改变，这一特性已经弱化，但是在数据的传输时，采用向量类型仍然能够获取一定的性能提升。

原则10如一个表达式在内核中重复出现，应考虑用临时变量存储，以避免多次计算造成的性能损失。

原则11避免不必要的barrier操作，在内核中barrier操作对性能影响很大，应考虑调优算法来减少barrier的使用。

上述是比较通用的11条编程原则。另外，还有一些需要注意的事项需在具体编码中根据测试和并行化编程特点具体进行分析才能决定。

同时，在编码过程中，合理地选择数据访问和传输方式也能够在一定程度上提升程序性能。不良的编码方式可能导致数据的重复复制，浪费带宽。而从图1中可以看出，数据的传输速率并不是很快。对于AMD平台来说，AMD的OpenCL编程手册[15]中根据不同的情况给出了建议，可以做为数据传输的参考。

3 优化及结果

本文采用Lammps自带的LJ力计算测试脚本进行测试，测试的粒子个数为262 144个，测试的步长分别为5 000和10 000步。

分别使用4CPU、4CPU加一个集成显卡(HD8650G，4CPU+1GPU)以及加两个显卡(HD8650G+HD8790M，4CPU+2GPU)三种情况进行测试，记录其总计算时间Time、LJ力计算用时占的百分比PT(Pair Time)、建立邻接表用时所占的百分比NT(Neigh Time)以及系统通信所占的百分比CT(Comm Time)。为了便于描述，将百分比部分的数据精度设定为一位，对于较小的数字采用直接设其为零。测试的初始结果如表2所示。

Table 2 Initial test results of LJ force表2 LJ力初始测试结果

可以看出，在只用CPU进行运算时，其主要的时间开销为LJ力计算部分以及邻接表的建立。而当使用GPU进行计算后，虽然在总时间上略少于只使用CPU进行运算，但是通信时间所占的比重增大了很多，这也导致邻接表建立的时间占运算总时间的比重微乎其微，如公式(3)所描述的那样弱化了p′带来的性能提升。同时，通过测试得到在LJ力计算部分加速比仅比使用4CPU的情况加速了1.2～1.24倍。本文后续将阐述对邻接表建立的研究及优化、LJ力计算研究及优化并给出优化后的结果进行对比。因原Lammps代码中，OpenCL加速部分是作为静态库进行调用的，这样每次更新测试时均需要对整个代码进行编译。为了方便，我们首先改动了OpenCL库的编译文件Makefile，使其生成动态库供Lammps主程序调用。

3.1 邻接表建立研究及优化

对于分子动力学模拟来说，仿真的粒子数目通常可以达到万、百万甚至更高。对每一个计算步来说，直接计算其他粒子对某一粒子的作用力，计算复杂度将达到O(n2)。从短程力本身具有截断特点出发，人们研究出了两种降低计算复杂度的方式，即元胞列表法和网格搜索法。

(1)元胞列表法:将系统中的所有粒子，划分成N*N*N的网格，这样只需计算每个网格中粒子与相邻网格的粒子之间的作用力便可，比如二维情况下只需进行8个邻近元胞的搜索，而三维情况下为27个。网格大小通常选择为截断半径rcut。

(2)网格搜索法：与元胞列表法类似，不同的是，不把邻近网格中所有的粒子都加入当前粒子的邻居列表，而是将相同或者相邻网格里的小于截断半径的粒子加入到邻居列表中，进一步减小邻居列表的长度。

Lammps使用网格搜索法进行粒子邻接表的创建，分两步进行，首先建立元胞列表，然后使用网格搜索法建立邻居列表。可以用二维的模型进行描述，如图2所示。

Figure 2 Neighbor-list building

将所有的粒子进行编号，并划分元胞区域。通过粒子当前坐标，更新粒子所在的元胞位置。在建立邻居列表时，首先更新元胞情况，以图2为例，搜索圆圈区域内部的粒子并加入到圆心粒子的邻居列表中。为了建立元胞列表，Lammps使用了基数排序算法。具体过程为将粒子所在的元胞编号作为关键字，粒子编号作为记录，按照关键字排序后，便可得出每个元胞中所具有粒子的有序表。我们首先使用OpenCL实现了一种并行基数排序算法。算法的核心是求前缀和(Prefix Sum)。需要说明的是，因邻接表的建立并不是程序主要耗时部分，对减少计算总时间并没有显著优势。

Lammps邻居列表建立部分OpenCL内核代码存储在neighbor_gpu_cl.h头文件中。优化内核实现代码工作如下：

(1)利用中间变量去除代码中求取元胞坐标的取余(%)操作。源代码中的计算过程为：

intix=BLOCK_ID_X+cells_in_cutoff;

intiy=BLOCK_ID_Y% (ncelly-cells_in_cutoff*2)+cells_in_cutoff;

intiz=BLOCK_ID_Y/ (ncelly-cells_in_cutoff*2)+cells_in_cutoff;

改进后过程为：

intix=BLOCK_ID_X+cells_in_cutoff;

inttmp=ncelly-cells_in_cutoff*2;

intdevide=BLOCK_ID_Y/tmp;

intiz=devide+cells_in_cutoff;

intiy=BLOCK_ID_Y-devide*tmp+cells_in_cutoff;

这里可以看出违反了原则10和原则4，通过定义一个临时变量存储中间结果以及调整计算顺序避免了取余操作。

(2)在查询粒子i对应的邻接元胞jcell的序号时，需要对三个坐标轴方向进行扫描，在原代码中采用了三重for循环进行计算，并且在最内层循环计算jcell，因计算jcell操作会带来很多连乘及累加操作，有一定的性能损失。元胞序号有一定的规律，第一个优化方式为使用序列值的规律进行简化，可以将三重for循环简化成一重for循环,jcell的计算也可以简化到加法运算。这在串行程序中，可以获得比较好的加速效果。但是，因循环过程有一些判断语句，在异构并行环境下反而造成了性能的损失，我们的测试也证明了这一点。通过分析，使用初始jcell，将jcell轮询中的变化分割到每层循环中，获得了较好的效果。源代码中计算过程为：

for (intnborz=nborz0;nborz≤nborz1;nborz++)

for (intnbory=nbory0;nbory≤nbory1;nbory++)

for (intnborx=nborx0;nborx≤nborx1;nborx++)

intjcell=nborx+nbory*ncellx+nborz*ncellx*ncelly;

end for

end for

end for

改进后过程为：

intnborz=nborz0,nbory=nbory0,nborx=nborx0;

inttmp2=ncellx*ncelly;

intjcell0=nborx0 +nbory0*ncellx+nborz0*tmp2;

intjcelly0=jcell0,jcellz0=jcell0;

intjcell=jcell0;

while(nborz≤nborz1)

while(nbory≤nbory1)

while(nborx≤nborx1)

//do scan

jcell++;

nborx++;

end while

nbory++;jcelly0+=nx;jcell=jcelly0;

end while

nborz++;

jcellz0+=tmp2;jcelly0=jcellz0;jcell=jcellz0;

end while

(3)根据原则9将源代码中部分可使用向量方式优化的代码进行优化，如坐标的运算，源代码采用的是标量方式进行计算。需要三条语句完成，而通过向量化操作后则只需一条语句即可实现。

3.2 LJ力计算研究及优化

OpenCL加速库中LJ力计算部分在lj_cl.h文件中。主要过程为根据查询需计算的i粒子邻接粒子j的范围，轮询该范围中的粒子信息。通过使用公式(4)中的Lennard-Jones势函数计算公式计算粒子间的作用力。

V(r)=4ε[(σ/r)12-(σ/r)6]

(4)

其中，ε为势能阱的深度，σ是相互作用的势能刚好为0时的两体距离，即截断半径rcut。这两个参数通过查找表得到。r为两粒子间的距离。对该部分内核的优化如下：

(1)根据原则1展开小规模循环操作。在内核代码中的store_answers、store_answers_q、k_lj、k_lj_fast部分可以发现多处已知边界的小循环。通过测定，相较原代码，仅展开操作所带来的LJ力计算用时性能提升可达到1.25～1.303倍。

(2)根据原则6将代码中部分可以使用内核函数优化的代码进行优化，如在代码中存在一些使用条件判断进行赋值的单行语句，可以使用原则6所举例子中的select内核函数对其进行优化。

(3)根据原则10将代码中重复计算部分通过提取到循环外部、使用临时变量等方式进行优化。

(4)根据原则9将代码中部分标量操作转换成向量运算形式。

3.3 优化结果

通过对短程力实现部分优化后再次测试得到的数据如表3所示。

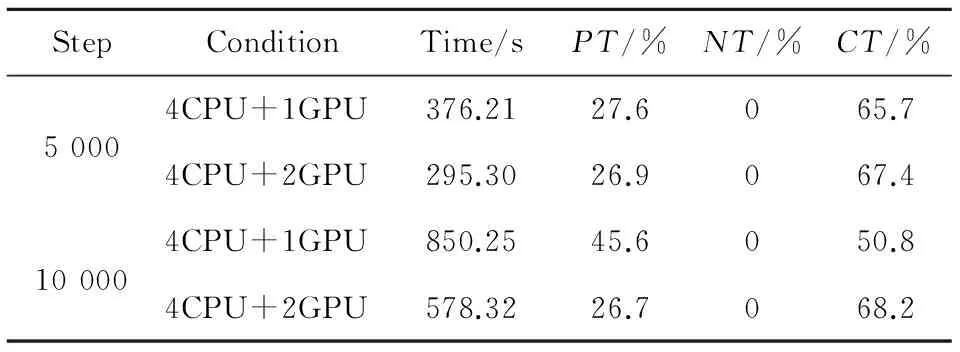
Table 3 LJ test results after optimization表3 LJ力优化后测试结果

对比发现，相较原OpenCL实现代码，改进后的总时间在使用单GPU测试时5 000步及10 000步分别达到了原来的1.3倍及1.72倍。而采用双GPU同时测试时，计算5 000步及10 000步分别达到了原来的1.39倍及1.74倍。对于LJ力计算部分，单GPU 5 000步提升了1.39倍，10 000步提升了1.48倍。双GPU 5 000步提升1.75倍，10 000步提升了1.79。邻接表建立部分代码单GPU最高提升1.35倍，双GPU最高提升1.64倍。

从上述结果可以看出，虽然GCN显卡架构从结构上使得GPU更加适用于异构编程，但通过合理的优化代码仍然能够在性能上有所提升。我们发现影响内核程序性能的主要原因在于原则1、原则8、原则9、原则11;而当特定语句如原则4、原则6、原则7、原则10中相关情况出现较多时，也会造成性能的损失；其他原则对性能的影响并不明显。其主要思想可以归结为减少冲突、增加访问带宽以及合理利用资源。另外，针对如邻接表建立中(2)中所述情况的特殊情况应合理调整计算方式。为最大化性能提升，可继续研究算法中可并行化部分，如本文中增加了邻接表部分基数排序算法的OpenCL实现。由于OpenCL内存模型中全局内存和本地内存读取速度差异较大，而本地内存所能够存储的信息容量一般为32 KB～64 KB，这在大规模分子并行模拟时，使得模拟粒子信息存储在全局内存中，加重了传输损耗，造成性能瓶颈。比较好的方式是，结合消息传递接口MPI(Message Passing Interface)进一步分冶，减小单节点负担，获得更好的性能提升，这在文献[2]中也有所体现。

4 结束语

本文首先归纳总结了在OpenCL内核编程中可以提升性能的一些原则，阐述了一种衡量异构平台情况下加速效果的理论公式。首先对Lammps短程力在Y485P平台下的加速效果进行了测试，然后通过研究Lammps分子动力学中的OpenCL短程力实现代码，根据总结出的内核代码编写原则进行优化，使得最终的总时间较原代码最高提高了1.74倍，LJ力计算部分较原代码最高提高了1.79倍，邻接表计算较原代码最高提高了1.64倍。证明通过合理优化内核代码能够提高其性能。

[1] Alder B J,Wainwright T E.Phase transition for a hard sphere system[J]. The Journal of Chemical Physics,1957,27(5):1208-1209.

[2] Li Bo-yang,Nie Feng-guang,Li Xiao-xia,et al.Performance test of lammps molecular dynamics simulation on GPU parallel computing cluster[J].Computers and Applied Chemistry,2011,28(10):1229-1233.(in Chinese)

[3] http://www.ks.uiuc.edu/Research/namd/.2014.

[4] http://ambermd.org/.2014.

[5] http://www.gromacs.org/.2014.

[6] Brown W M,Wang P,Plimpton S J,et al. Implementing molecular dynamics on hybrid high performance computers-short range forces[J]. Computer Physics Communications,2011,182(4):898-911.

[7] Brown W M,Kohlmeyer A,Plimpton S J,et al. Implementing molecular dynamics on hybrid high performance computers-particle-particle particle-mesh[J]. Computer Physics Communications,2012,183(3):449-459.

[8] Brown W M,Yamada M. Implementing molecular dynamics on hybrid high performance computers—Three-body potentials[J]. Computer Physics Communications,2013,184(12):2785-2793.

[9] Davis S,Loyola C,González F,et al. Las palmeras molecular dynamics:A flexible and modular molecular dynamics code[J]. Computer Physics Communications,2010,181(12):2126-2139.

[10] Jia Hai-peng,Zhang Yun-quan, Long Guo-ping, et al. Research on Laplace image enhancement algorithm optimization based on OpenCL[J]. Computer Science, 2012,39(5):271-277.(in Chinese)

[11] Jiang Li-yuan,Zhang Yun-quan,Long Guo-ping, et al. Parallelism and research on functions with continuously independent data and intensive memory access using OpenCL[J]. Computer Science, 2013,40(3):111-115.(in Chinese)

[12] Pang Xu,Zhang Yun-quan,Long Guo-ping, et al. Research on mean shift algorithm using OpenCL on multiple many-core platforms[J]. Computer Science, 2013,40(3):79-85.(in Chinese)

[13] Khronos OpenCL Working Group. The OpenCL specification,version 1.2,revision 16[S]. 2011.

[14] Daga M,Aji A M,Wu Chun-feng. On the efficacy of a fused CPU+GPU processor (or APU) for parallel computing[C]∥Proc of 2011 Symposium on Application Accelerators in High-Performance Computing (SAAHPC),2011:141-149.

[15] AMD.AMD accelerated parallel processing OpenCL programming guide[Z].2013.

附中文参考文献：

[2] 李伯杨,聂峰光,李晓霞,等. GPU 并行计算集群上的 LAMMPS 分子动力学模拟性能测试[J]. 计算机与应用化学,2011,28(10):1229-1233.

[10] 贾海鹏,张云泉,龙国平,等. 基于 OpenCL 的拉普拉斯图像增强算法优化研究[J]. 计算机科学,2012,39(5):271-277.

[11] 蒋丽媛,张云泉,龙国平,等. 基于 OpenCL 的连续数据无关访存密集型函数并行与优化研究[J]. 计算机科学,2013,40(3):111-115.

[12] 庞旭,张云泉,龙国平,等. 基于 OpenCL 的均值平移算法在多个众核平台的性能优化研究[J]. 计算机科学,2013,40(3):79-85.

赵成龙(1989-),男，江苏徐州人，硕士生，研究方向为计算机系统结构。E-mail:Zhaochenglong08@126.com

ZHAO Cheng-long,born in 1989,MS candidate,his research interest includes computer architecture.

Short-range force algorithm optimization in Lammps based on OpenCL

ZHAO Cheng-long1，SHI Hui-bin1，YU Xin-feng2

(1.College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016;2.College of Computer Science and Technology,Nanjing University of Science and Technology,Nanjing 210094,China)

Lammps is a widely used open source software for molecular dynamics simulations and related issues, through which we can understand solid and liquid nature. It enables the CUDA and the OpenCL to accelerate calculation. Since the OpenCL has cross-platform features, it becomes a research focus. We summarize the OpenCL kernel programming principles and propose an improved Amdahl's law which can measure the acceleration performance on heterogeneous platforms. The short-range force algorithm in Lammps on Y485P platform is tested. We achieve better acceleration effect by optimizing the kernel source codes of the key parts, such as neighbor-list building and short-range force calculation.

GPU;Lammps;OpenCL;molecular dynamics;short-range force;kernel optimization

1007-130X(2015)09-1614-07

2014-08-25;

2014-10-31

TP302

A

10.3969/j.issn.1007-130X.2015.09.002

通信地址：210016 江苏省南京市秦淮区御道街29号南京航空航天大学计算机科学与技术学院

Address:College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,29 Yudao St,Qinhuai District,Nanjing 210016,Jiangsu,P.R.China