内模解耦控制在中央空调系统的应用

王延年，张 帅

（西安工程大学 电子信息学院，陕西 西安 710048）

近年来，我国工业正处于不断发展的阶段。改善工厂环境、提高节能控制效果已经成为当前国内外智能工业领域研究的热点问题。然而中央空调控制系统是一个多变量、大滞后、大惯性系统，特别是空调系统具有非线性、强耦合特性，和多参数控制存在变量耦合问题成为了空调控制研究中的重点。目前国内外在这方面的研究很少，国内外对中央空调系统中主要采用模糊PID控制技术、神经网络PID控制技术等，这种控制技术不足之处是对于工况和环境变化的适应性差，对大时滞和强耦合控制对象的控制效果也不理想[1]。

针对中央空调控制系统中对温度的控制和湿度控制存在强耦合问题[2]，且难于稳定运行的情况，提出内模解耦控制方案。通过引入多变量内模控制系统，对多变量系统进行解耦，解耦后的子系统变为单变量系统[3]。此方案能够消除时滞带来的不利影响，完成解耦，调节时间短且超调量小，控制精度高，抗扰动性能好。通过理论分析和实验表明，该控制器使得解耦后的多变量系统具备良好的动、静态特性，提高了控制的精度和稳定性，达到了理想的控制要求。

1 空调系统的温湿度耦合特性分析

空调系统是一个多变量的控制系统，多个变量之间必存在着某种程度的相互影响。轻度耦合是可以被接受的，但是较为严重耦合会导致系统运行不稳定。对于空调系统中温度、湿度这两个参数，常常是同时需要调节，且两个量之间相互影响、相互制约。如果空调区域内的温度升高，将会导致相对湿度降低；温度降低，也会引起相对湿度升高。因此，在调节过程中对某一参数的调节常常会引起其它的一些参数变化。

针对这种温湿度耦合特性，就需要在设计空调的控制系统时要选用适当的控制方法，既能够使控制器稳定工作，又能让每个独立的控制回路正常工作，把回路间的相互耦合作用控制在我们能够接受的范围内[4]。

2 内模解耦控制

2.1 内模控制基本原理

图1是多变量内模反馈控制系统的基本结构，其中C（s）为解耦内模控制器，G（s）为被控对象传递函数矩阵，Gm（s）为内部模型，u（s）为控制系统输入，R（s）为系统输入，Y（s）为系统输出，D（s）为干扰信号，E（s）为控制系统偏差，D（s）为系统输出与过程模型输出之差。C（s）和Gm（s）组成了整个内模控制系统的结构，都可以用模拟硬件和计算机软件实现。正是因为此结构包含了除了控制器C（s）以外的对象模型Gm（s），所以内模控制因此而得名[5]。

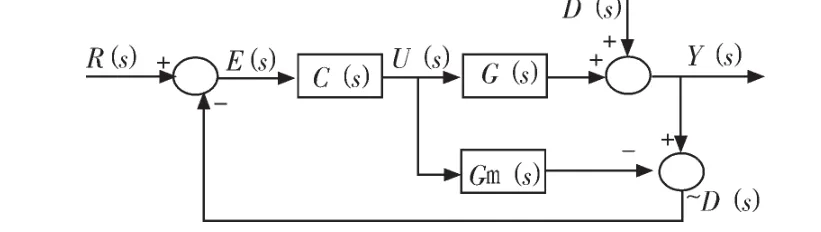
图1 内模控制系统框图Fig.1 Internal model control system block diagram

由图1可以得到闭环系统的输入和输出方程为

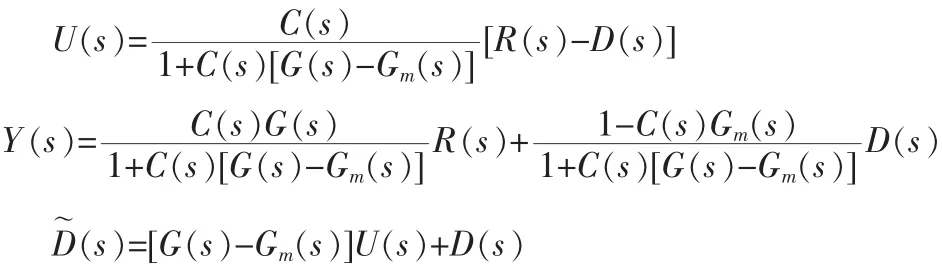
2.2 多变量解耦内模分析

在 模 型 匹 配 的 条 件 下 ， 即 G（s）=Gm（s），G（s）=Gm（s）=

式中，gi=gij0（s）e－τijs为正则有理分式，τij为非负常数，i，j∈n={1，2，…，n}。

由图1可以得到系统输入输出间的闭环传递函数矩阵为

假设 H（s）=G（s）C（s）=diag{hii（s）}，对于 G（s）C（s）的每一列有

式中，c*i（s）为 C（s）的第 i列元素；ei为第 i个标准基。

设 Gij（s）为对应 gij0（s）e－τijs的 G（s）的代数余子式，则 adjG（s）=[Gji（s）]是 G（s）的伴随矩阵，det G（s）为 G（s）的行列式，于是得到

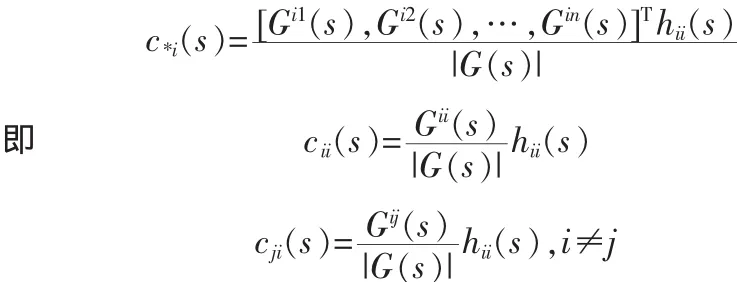
说明IMC控制器的对角元素cii唯一决定了其非对角线元素cij。

综上，解耦后的IMC控制系统闭环传递函数为

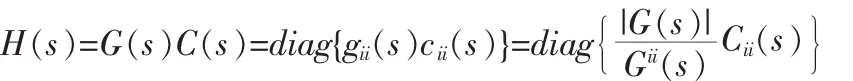
单纯从理论上分析，单回路过程的IMC设计方法同样适用于多输入输出系统，根据解耦后的函数形式的等价过程的gii来设计cii。可是在大部分情况下，gii不是有理传递函数加纯滞后这一形式。所以直接推算出来的控制器非对角元素cij可能是附加时滞和非最小相位零点到控制器对角元素cii[6]。

2.3 多变量解耦内模控制器设计方法分析

根据上面的分析，在设计多变量内模控制器时，分别对系统时滞条件和非最小相位零点进行分别系统分析。

gii的一般形式可表示如下：

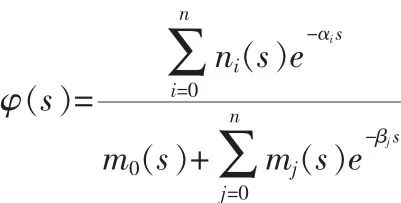
定义 φ（s）的时滞为 τ（φ－1（s））=α0，那么对于任意非零式φ1（s）、φ2（s）和 φ（s）有，τ（φ－1（s））=－τ（φ（s）），τ（φ1φ2）=τ（φ1）+τ（φ2）成立。

若 τ（φ（s））≥0，表示 φ（s）从输入阶跃信号开始到有非零值输出时所需要的时间。若τ（φ（s））≤0，则表示未来的某时刻的输入值可以决定系统的输出。对于任何可实现且非零的φ（s），τ（φ（s））都不可以取负。

所以，对于可以实现的C（s）必须满足：

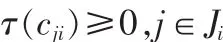
其中，Ji={j∈n|Gij≠0|}可推得

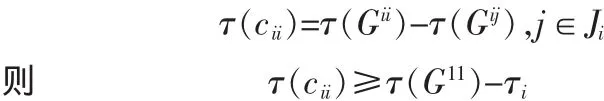
此公式表示的是控制器对角元素的时滞条件，表示控制器的第i个对角元素所必须包含的最小时滞。

H（s）=G（s）C（s）的元素 hii=giicii满足

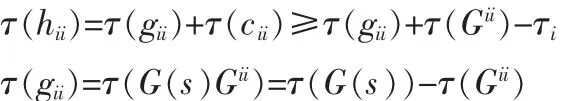
根据以上两个式子，推出

表明系统解耦后的第i个回路闭环传递函数所必需包含的最小时滞，称为解耦后闭环传递函数的第i个回路所包含的时滞特性条件[7]。

如果考虑被控对象是具有s平面右半部零点的非最小相位系统，其传递函数为G（s）。

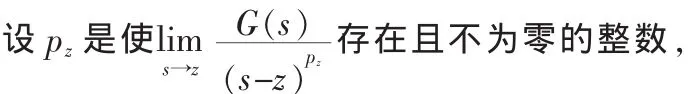
如果 pz＞0，则在 s=z处 G（s）有 pz个零点，如果 pz＜0，则在s=z处 G（s）有 pz个极点，如果 pz=0，则在 s=z处 G（s）无零极点。

所以，C（s）稳定就必须满足：

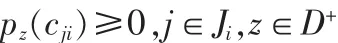
对于∀z∈D+，有 pz（Gij）≥0，即 pi（z）≥0，

所以有

得，cii不需要有z∈Z+Gii以外的非最小相位零点。

cii的非最小相位零点用下式表示：

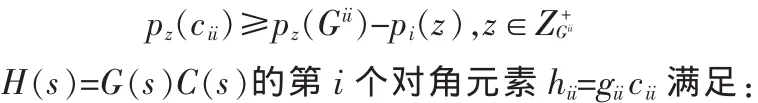
Pz（hii）=pz（giiCii）=pz（gii）+pz（Cii） ≥pz（gii）+pz（Gii） －pi（z），∀z∈D+

由以上得到，hii的非最小相位零点用下式表示：

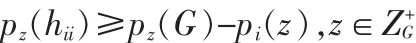
3 控制实验讨论与分析

根据工程数据显示，控制目标保证中央空调室内温度定为（22±1）℃，湿度为65%±5%。根据某中央空调安装设备公司数据，采用二阶系统模型进行分析研究。根据表中参数，可得被控对象传递函数矩阵为

首先，利用PID参数整定方法计算出各回路的最优PID控制参数，将此参数运用到对角线解耦网络当中，且在空调区域温度回路加入时间间隔1 500 s幅值范围在－5～5℃的随机扰动，实验效果如图2所示。

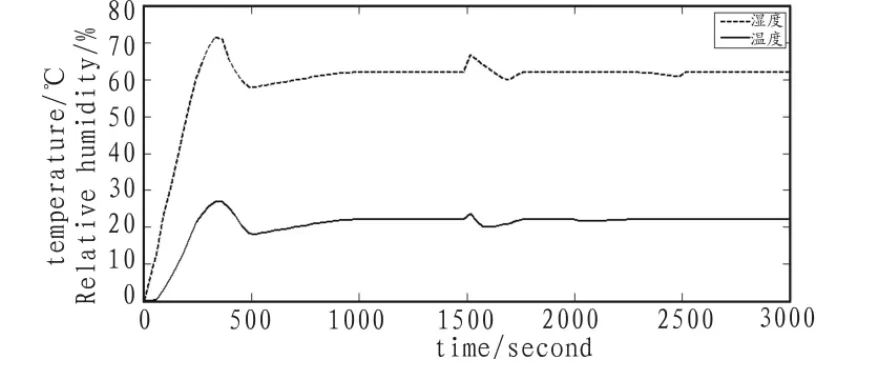
图2 PID解耦分析图Fig.2 PID decoupling analysis diagram

从图2中看到，虽然温湿度间基本实现了系统解耦，但是输出响应曲线还不是很平滑，会有间断性的波动。而且当温度受到扰动时，湿度在经过一段时间的延迟后也被这个扰动所影响。说明运用对角线解耦控制后的控制系统还是存在耦合，并且对扰动非常敏感，因此对角线解耦没有达到消除空调区域温度和含湿量耦合的目的。

然后，运用多变量解耦内模控制方法来控制空调系统输出的效果如图3所示。

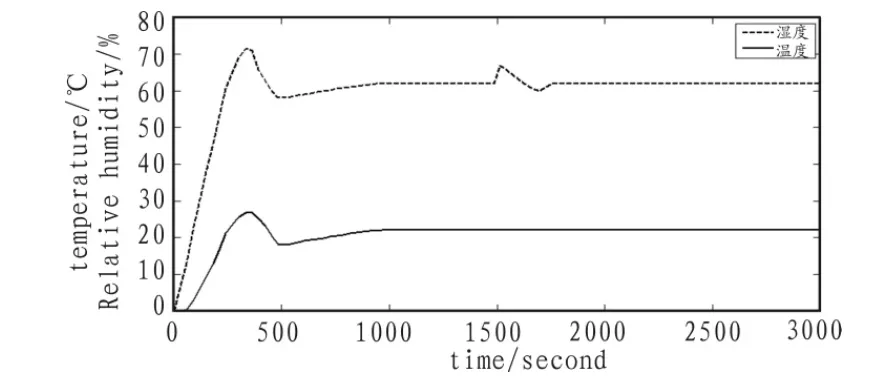
图3 多变量内模解耦分析图Fig.3 Multivariable internal model decoupling analysis diagram

从图3中看出多变量解耦内模方法不仅实现了各回路之间的解耦控制，而且在输出响应上升过程中没有超调，曲线平滑。从图2到图3，系统输出响应都存在一定的滞后，这可以理解成系统的输出要经过一段时间才能够跟踪设定值，这在实际当中也是正常情况。

从以上两个实验图来看，内模控制的效果要优于PID控制，没有超调且稳定快速性好。在加入外部扰动后，PID控制输出的扰动峰值要大于内模控制，而且PID控制恢复到设定值的时间要长于内模控制。说明解耦内模控制可在同一参数下适应多工况运行，且控制效果较好。

4 结 论

通过引入多变量内模控制方法，对多变量系统进行解耦，解耦后的子系统变为单变量系统，解决了常规PID控制器用于强耦合系统中的不足。实验结果表明，该控制方案不但解决了温湿度耦合问题，提高了调节过程的动、静态性能；同时改善了系统的适应性、稳定性和实时控制性。从而保证了工厂内温湿度的精确、稳定控制，获得了较好的控制效果。

[1]李令言．中央空调节能控制系统的研究与开发 [D]．合肥：中国科学技术大学，2011．

[2]张斐斐．多变量内模解耦控制研究[D]．吉林：东北电力大学，2012．

[3]Matthew C T，Sophie T．Anti-windup compensation for systems with sensor saturation:a study of architech and structure[J]．Internation Journal of Control，2009，20（2）:1677－1684.

[4]丁良．两自由度内模控制和解耦内模控制[D]．杭州：浙江理工大学，2012．

[5]GUO Qing，YU Zhang， Min-Sen Chiu.Decoupling internal model control for multivariable system with multiple time delay[J].Chem.Eng.Science，2002，57（3）:115－124.

[6]袁琴．多变量系统内模控制方法研究[D]．北京：北京化工大学，2008．

[7]陈娟，潘立登，曹柳林．多变量时滞过程的解耦内模控制及应用[J]．北京化工大学学报，2007（3）:98－102．CHEN Juan，PAN Li-deng，CAO Liu-lin.Multivariable timedelay decoupling internal model control and the application of the process[J]．Journal of Beijing University of Chemical Industry，2007（3）:98－102．