基于改进NLMS算法的谐波电流检测方法

张文兵，赵镜红，吴旭升，高键鑫

(海军工程大学电气与信息工程学院，武汉430033)

0 引言

近年来，随着科技的飞速发展，电力网络中，以整流器、变频器和其他各种电力电子设备为主的非线性负载使电力网络受到了严重的污染。有源电力滤波器作为谐波抑制的有效手段，在研究中取得了明显的发展[1]。谐波检测技术是有源电力滤波器主要的性能指标之一，所以它一直是有源电力滤波器技术的研究重点。

从自适应对消原理[2]的提出，它就受到各领域的专家和学者的广泛研究，随后有人提出了最小均方误差准则，由于该算法结构简单，自适应学习能力较强的特点，在电力网络谐波检测中的应用越来越多。而传统定步长 LMS算法很难满足收敛速度快和稳态误差小的目标，为了实现这个目标，有学者提出了一种变步长 LMS算法。如文献[3]中变步长的思想就是在步长因子和均方误差之间建立一种线性关系，即步长因子的大小随着误差的大小变化而变化。算法开始时，误差较大，而此时步长因子也大，则收敛速度就很快，当误差越来越小，步长因子也就越来越小，当误差趋近于零时，步长也趋近于零，保证了较小的稳态误差。但该算法抗干扰能力差，当输入信号突变时，会导致系数的突变，使系统的稳定变差。为了解决输入信号突变时带来的系统系数突变，使得 LMS算法性能进一步提高，归一化最小均方（NLMS）自适应滤波算法被提出，该算法比 LMS有更好的鲁棒性且易于使用。它的成功应用关键在于如何选取可以折中算法的收敛速度和稳态误差的步长。而如何选取最有且可靠的步长一直是一个难点，在现如今众多选取步长的策略中，都是采取变步长的方法。通过对文献[4-5]分析发现，尽管算法收敛速度的问题通过变步长算法得到了解决了，但是由于时变的步长不能收敛到零，而且大部分情况下步长大小是一个未知的数，所以很难确定最终稳态误差的大小。

为此本文提出了将 LMS算法引入动量项的思想[6]融入到NLMS算法的谐波电流检测方法，该方跟传统NLMS的方法的不同之处就是使用了两个步长参数（步长因子μ和动量步长β）来调整动态响应速度和稳态精度之间的平衡问题。即给定一个较小的步长因子μ来保证高的稳态精度的同时，通过调节时变的动量步长β来加快谐波检测的响应速度，很好的解决了谐波电流检测法的动态响应速度和稳态精度之间的平衡问题。

1 谐波电流检测模型

图1是一个典型的基于自适应噪声对消技术的谐波电流检测框图[7]。其中，负载电流iL(n)是主要输入，x(n)作为参考输入，是负载电流基波频率的单位正、余弦信号，即

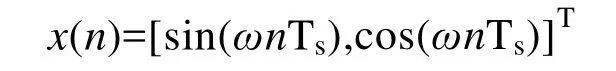
一般由锁相环（PLL）从电源电压us(t)处获得，记x(n)=[x1(n),x2(n)]T,w(n)为其对应的权系数，记为w(n)=[w1(n),w2(n)]T,ω为角速度，Ts为采样周期，n为采样时刻，T为数学转置运算符。

设us(t)=sin(ωt),即为标准的正弦电压,其中角速度ω=2πf（f为频率）。对负载电流iL(n)进行傅立叶级数展开如下式：

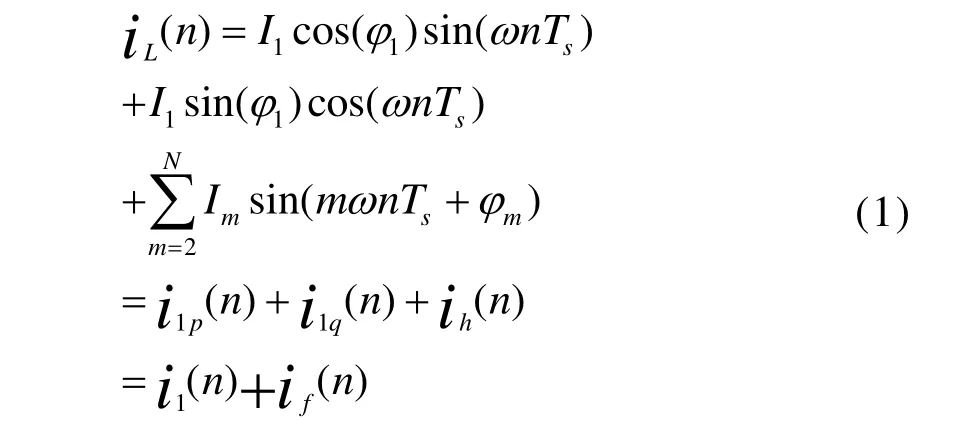
上式中m代表谐波次数，最高次数为N；i1为基波电流，if是基波无功电流i1q和谐波电流ih之和，i1p是基波有功电流。

基于自适应噪声对消技术的谐波电流检测就是权系数w(n)使用某种自适应算法进行实时更新，用于跟踪负载基波电流i1,使滤波器输出y(n)通过公式（2）在自适应算法稳定后无限逼近i1，然后通过公式（3）就可以得到谐波电流ih的逼近值e(n),达到了检测出谐波电流的目的。

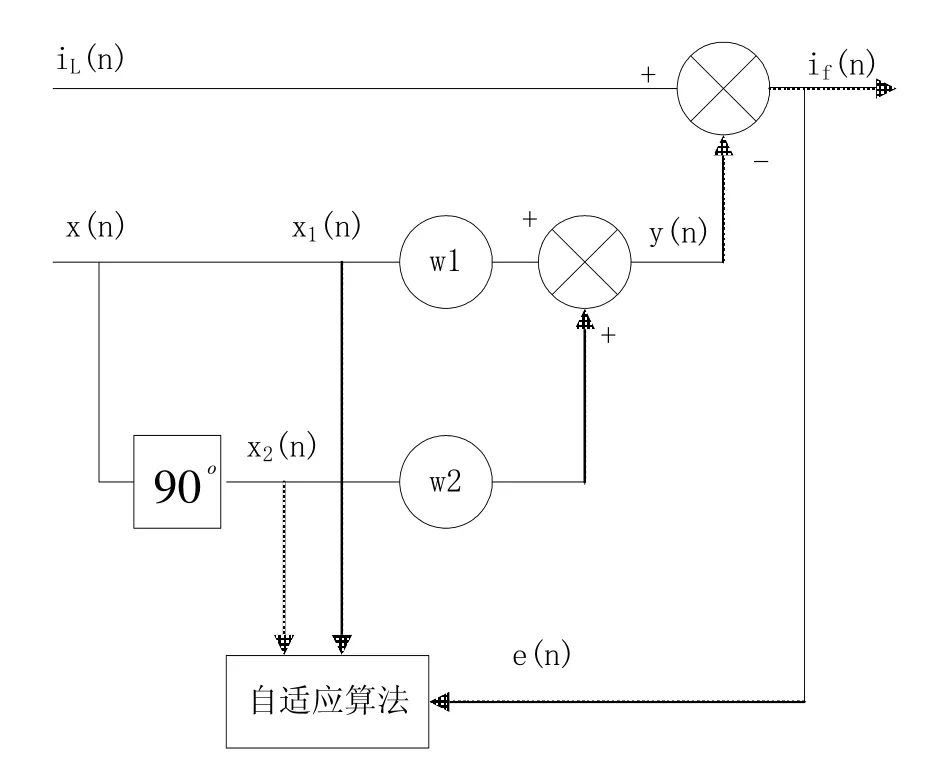
图1 谐波检测原理框图

2 算法原理

2.1 NLMS算法原理

NLMS算法是在 LMS算法的基础上发展而来的，解决了 LMS算法因为输入信号的突然改变而造成权系数w(n)的突变，从而影响系统稳定的问题。LMS算法的数学表达式如公式(2)-(5)：

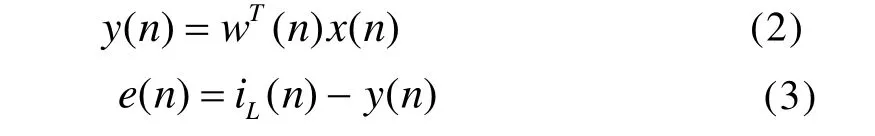
权系数的更新表达式，如下：

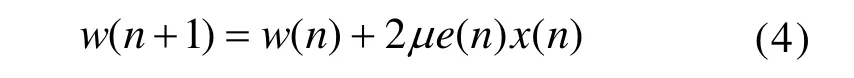
其中，步长因子μ的约束条件为[2]：

五是加大社区矫正心理矫治工作的宣传力度，争取社区服刑人员亲友的理解与支持，向这些身边人普及心理健康常识，协助“定位”社区服刑人员的心理状态，用亲情友情感化社区服刑人员，帮助社区服刑人员重塑人生，回归社会。

为了确保算法的收敛性，μ就应该在公式(5)所示的范围为内选值，λmax是输入信号相关矩阵R=E[x(n)x(n)T]的最大特征值。

NLMS算法就是在 LMS算法基础上采用了可变因子，归一化输入向量，使瞬时误差最小化。

在公式(4)所示的权系数更新过程中，权系数可改为：

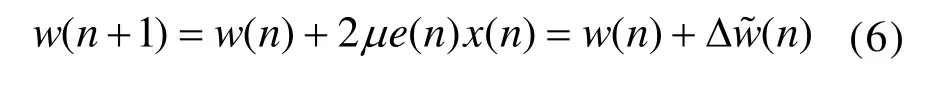
为了使算法收敛时，瞬时误差尽可能小，瞬时误差可用下式表示：

若权系数可以由下式表示：

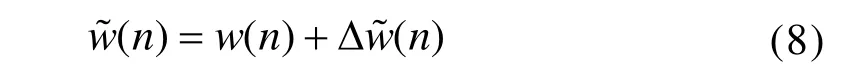
将式(8)代入式(7)得[2]：

为了加快算法收敛，则须得到最佳步长，使Δe2(n)最小。式(10)对步长求导得：

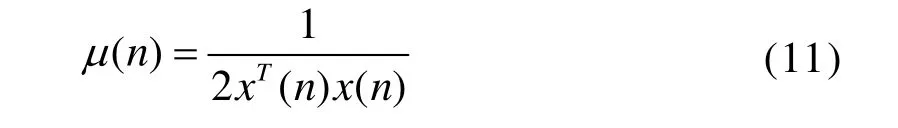
所以LMS的权系数更新方程变为：

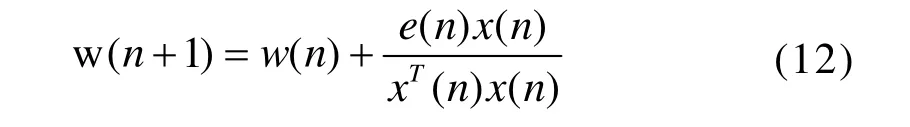
实际应用中，更新方程中会引入两个固定的参数，步长因子μ和正则化因子δ，所以就得到了NLMS算法的更新方程，如下：

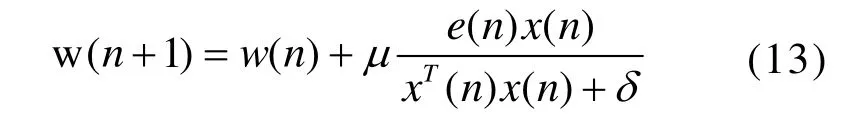
上式中步长因子μ的取值为 0<μ<2，NLMS算法对输入信号进行了归一化，因而该算法相对于 LMS算法有很好的鲁棒性，解决了输入信号突变带来的系统不稳定为问题。但是依然存在步长大小选取和稳态误差大小之间的问题。

2.2 MLMS算法原理

动量项最小均方算法(MLMS)[6]也是在 LMS算法基础上改进而来，因为按照经验 LMS算法的步长一般选取的比较小，而这样导致了收敛速度非常慢。为了解决这个问题，加快收敛速度，在式(4)权系数的更新的基础上添加一个[8]或多个动量项，就得到了多步阶梯下降算法的权系数更新方程，如下式：

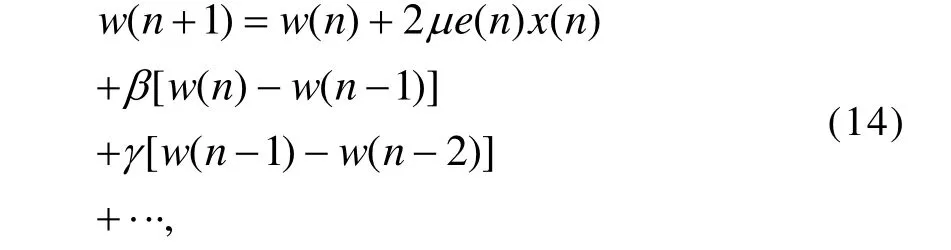
上式中β，γ，…和μ一样，都是步长参数。虽然该算法可以在一定程度上提高收敛速度，但是却使算法的稳态误差变大了。同时该算法成功应用的关键在于多个步长参数的选取，而通过查找文献到目前为止还没有很好的方法，导致了该算法的实用性太差。

2.3 改进的算法原理

步长在自适应算法中具有非常重要的作用。为了提高收敛速度，需要较大的步长参数，为了保证稳定性和减小稳态误差却需要较小的步长参数。为了解决NLMS算法的稳态误差无法控制和多步阶梯下降算法实用性太差的问题。本文通过将多步阶梯下降算法思想和 NLMS算法结合起来，提出了基于多步阶梯下降的NLMS算法。w(n)的更新方程为：

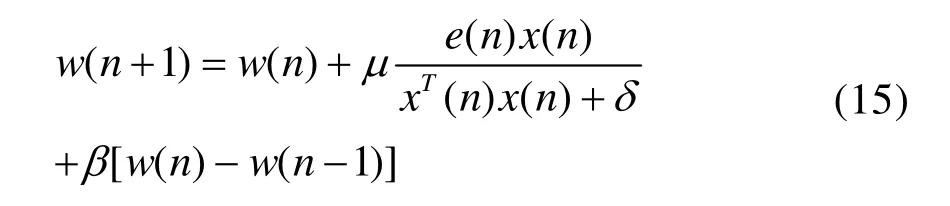
上式中有两个步长参数梯度步长μ和动量步长β。相对于传统的 NLMS算法(13)，改进的算法(15)中多了一个动量步长β。因为 NLMS算法的步长一般按照经验选取的非常小，这样收敛速度就会变得很慢，通过引入动量步长β来提高收敛速度，并能保证在算法收敛后具有较小的稳态误差。改进的算法是在NLMS基础上引入MLMS的思想，所以该算法的梯度依然使用归一化的输入信号，从而继承了传统NLMS算法较好的鲁棒性。

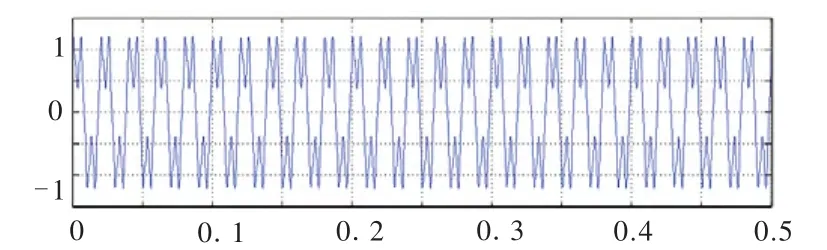
图2 负载电流曲线

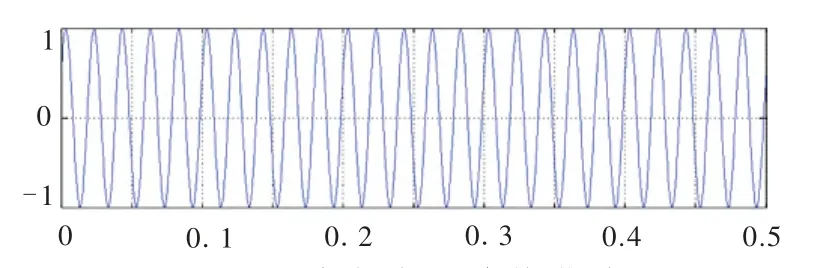
图3 基波电流理论值曲线

3 仿真分析

本实验主要是为了验证上述改进的NLMS算法在谐波电流检测中优势分析，即在NLMS的基础上引入一个受控动量项β后，在提高收敛速度的同时保证较小的稳态误差。

在 Matlab R2011b软件环境下对改进型NLMS算法的谐波电流检测方法进行仿真分析。实验中，负载电流[7]如式(6)所示，其中，ω=2πf=100π；采样频率为 10 kHz,滤波器的权系数w(n)初值为 0，参考输入x(n)为单位正，余弦信号。

从图5中可以看出，在μ一定的情况下，不同的β所对应的收敛速度和稳态误差。其中β=0

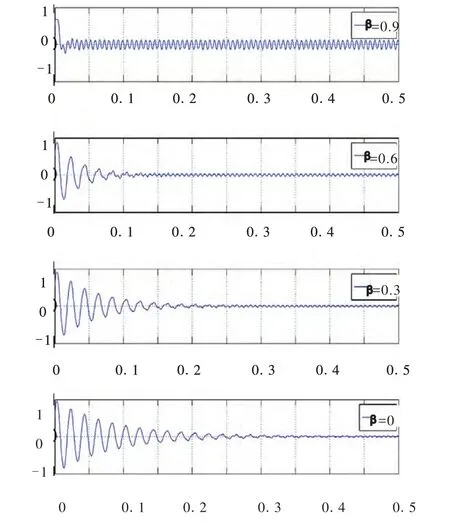
图5 取μ=0.04时,选取不同β所对应的基波电流检测值与理论值的误差曲线

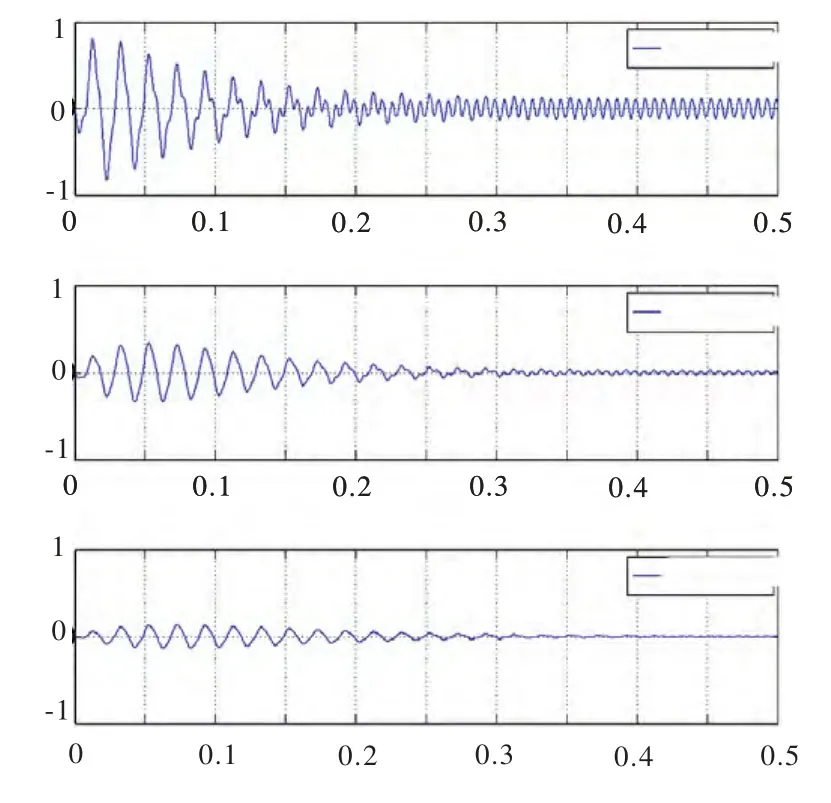
图6 取μ=0.04时,选取不同β＞0所对应的误差曲线与β=0的误差曲线的比较

所对应曲线是传统的NLMS算法，在μ=0.04的小步长下，算法的稳态误差很小，但是收敛速度却很慢。当β值逐渐增加时，收敛速度有明显的提高，β=0.9时算法的收敛速度很快，但是稳态误差也明显增加了。图6通过比较β=0与其他三个不同β值时的误差曲线，发现在β=0.3,β=0.6时，稳态误差大小与β=0的很接近，而收敛速度有很大提升，其中β=0.6的收敛速度大于β=0.3的收敛速度。从而验证了，在NLMS的基础上引入一个受控动量项β后，在提高收敛速度的同时保证较小的稳态误差。

4 结论

本文针对传统的NLMS算法的谐波电流检测方法在步长μ较小的情况下，虽然有较小的稳态误差，但是算法收敛速度很慢的问题，提出了一种改进型NLMS算法的谐波电流检测方法。该方法通过引入一个受控动量项β，对动量项进行调整来加速算法的收敛速度，并且在算法收敛后不影响算法最终较小的稳态误差。最后，用过仿真证明了本文所提出的改进算法的正确性及本文算法应用的有效性。

[1]王兆安，杨君，刘进军.谐波抑制和无功功率补偿[M].北京：机械工业出版社，1998.

[2]刘郁林.自适应算法与实现(第二版)[M].北京：电子工业出版社，2004.

[3]刘传林.电网畸变电流自适应检测方法[D].武汉：武汉大学，2012.

[4]Huang H-C,Lee J.A new variable step-size NLMS algorithm and its performance analysis [J].IEEE Trans Signal Process,2012,60: 2055-2060.

[5]Benesty J,Rey H,Vega L R,et al.A nonparametric VSS NLMS algorithm [J].IEEE Signal Process Lett,2006,13: 581-584.

[6]刘国海，张懿.一种新的变步长MLMS谐波电流检测法[J].电气传动，2009，39(2):44-47.

[7]喻翌，赵海全，何正友.基于 ANCT和 Adaline两种自适应谐波电流检测模型分析[J].电力系统保护与控制，2013，41（16）：71-76.

[8]马立新，王玉珠，孙进等.引入动态因子的改进MLMS谐波检测算法[J].电力系统及其自动化学报，2013，25(4)：18-21.

[9]陈瑞松，何政平，李圣清等.基于改进型SVLMS算法的谐波电流检测方法[J].大功率变流技术，2014，1：57-60.

[10]韩刚，孟庆辉.两种自适应噪声抵消算法的性能仿真[J].舰船电子工程，2014，34(2)：79-81.